النهايات والاتصال

نتاجات الدرس : 
- إيجاد نهاية اقتران عند نقطة بيانياً وعددياً وجبرياً .
- البحث في اتصال اقتران عند نقطة.

إيجاد النهايات بيانياً وعددياً: 
النهاية عند نقطة: اذا كانت قيمة الاقتران f(x) تقترب من قيمة واحدة L عندما تقترب x من c ، فإن نهاية f(x) عندما تقترب x من c هي L .

$\underset{x\to c}{lim}f\left(x\right)=L$

تقرأ: نهاية الاقتران f(x) عندما تقترب x من c هي : L 

النهاية من الجهتين: تكون النهاية f(x) موجودة عندما تقترب x من c ، إذا وفقط كانت النهايتان من اليمين واليسار موجودتين ومتساويتين.

$\underset{x\to c^{-}}{lim}f\left(x\right)=\underset{x\to c^{+}}{lim}f\left(x\right)=L \mathrm{إذا} \mathrm{وفقط} \mathrm{إذا} \underset{x\to c}{lim}f\left(x\right)=L$
 

---

مثال (1): إذا كان $f\left(x\right)=\frac{x^2-1}{x-1}$ ، فجد $\underset{x\to 1}{lim}f\left(x\right)$ بيانياً وعددياً: 

الإجابة:

أولاً : إيجاد النهاية بيانياً .
إن مجال الاقتران $f\left(x\right)=\frac{x^2-1}{x-1}$ هو مجموعة الاعداد الحقيقية R ما عدا (1)
وبما أنّ: $f\left(x\right)=\frac{x^2-1}{x-1}=\frac{(x-1)(x+1)}{x-1}=x+1$

فان التمثيل البياني للاقتران f(x) هو نفسه التمثيل البياني للمستقيم y=x+1 مع دائرة صغيرة غير مظللة عند x=1 كما في الشكل المجاور . 

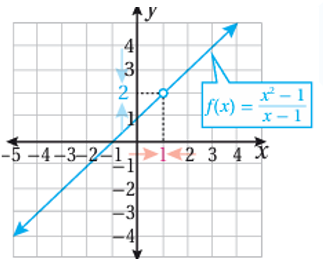
نلاحظ من التمثيل البياني أنه كلما اقتربت قيم x من العدد (1) من الجهتين ، فإن قيم f(x) المقابلة لها تقترب من العدد (2) من الجهتين ، وهذا يعني أن:

$\underset{x\to 1}{lim}\frac{x^2-1}{x-1}=2$

ثانياً : إيجاد النهاية عددياً .
ننشىء جدول قيم باختيار قيم x القريبة من العدد 1 من كلا الجهتين ، وإيجاد قيم f(x) المقابلة لها باستعمال الآلة الحاسبة.

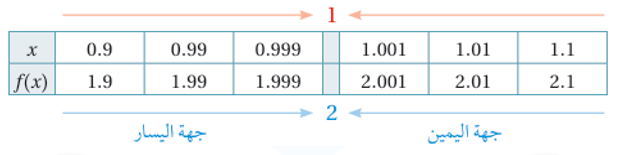
نلاحظ أيضاً أنه كلما اقتربت قيم x من العدد 1 من الجهتين ، فأن قيمة f(x) المقابلة لها تقترب من العدد 2

وهذا يعني أن: $\underset{x\to 1}{lim}\frac{x^2-1}{x-1}=2$

اذن ، النهاية متساوية في كل من الطريقتين .

---

مثال (2) : اذا كان $H\left(x\right)=\left\{\begin{array}{l}2x+2 , x<1\\ 2x-4 , x\ge 1\end{array}\right.$ ، فجد $\underset{x\to 1}{lim}H\left(x\right)$  

الإجابة:

أولاً : إيجاد النهاية بيانياً.
إن الاقتران H(x) متشعب ، ونمثله بيانياً كما في الشكل المجاور .
نلاحظ من التمثيل البياني أنه كلما اقتربت قيم x من العدد (1) من جهة اليسار ، فإن قيم H(x) المقابلة لها تقترب من العدد (4) ، وهذا يعني أن: $\underset{x\to 1^{-}}{lim}H\left(x\right)=4$

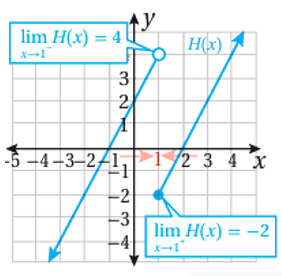
ونلاحظ أيضاً إن كلما اقتربت قيم x من العدد (1) من جهة اليمين، فإن قيم H(x) المقابلة لها تقترب من العدد (2-) وهذا يعني أن: $\underset{x\to 1+}{lim}H\left(x\right)=-2$
وبما ان النهايتين من اليمين ومن اليسار غير متساويتين، فإن $\underset{x\to 1}{lim}H\left(x\right)$  غير موجودة .

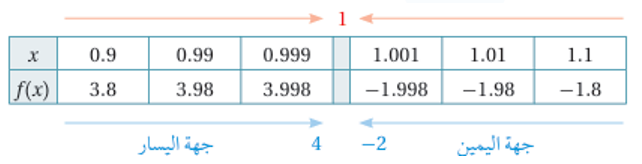
ثانياً : إيجاد النهاية عددياً: 
نلاحظ أن كلما اقتربت قيم x من العدد 1 من جهة اليسار فإن قيم H(x) تقترب من العدد 4 وكلما اقتربت من اليمين تقترب من العدد -1  ، وبما أن النهايتين من اليمين واليسار غير متساويتين ، فإنّ: $\underset{x\to 1}{lim}H\left(x\right)$ غير موجودة.

 

- تدريب: جد كلاً من النهايات الآتية بيانياً و عددياً : 

1) $\underset{x\to 3}{lim}(x+7)$            2) $\underset{x\to 0}{lim}f\left(x\right) , f\left(x\right)=\left\{\begin{array}{l}x , x\le 0\\ 1 , x>0\end{array}\right.$

---

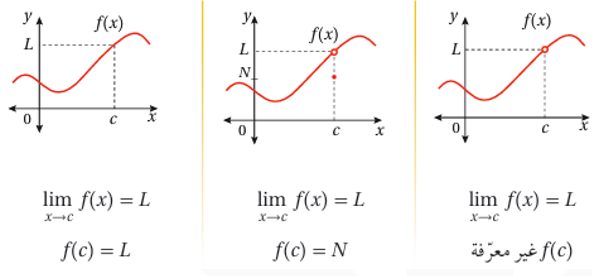
أن نهاية f(x) عندما تقترب x من العدد c لا علاقة لها بقيمة f(c) ، فمثلاً : 

$\underset{x\to c}{lim}f\left(x\right)=L$ في الحالات الثلاث الآتية:

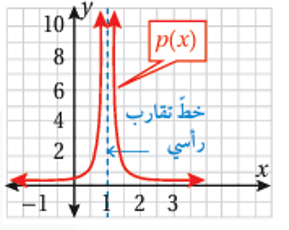
نهايات تتضمن (المالانهاية) :  في بعض الأحيان ، تكون النهاية من اليمين أو اليسار (أو كليهما) غير موجودة عند قيمة ما ،  لأن الاقتران يزداد أو ينقص بصورة غير محدودة  قرب تلك القيمة . وفي هذه الحالة ، نصف سلوك الاقتران بأنه يقترب من (المالانهاية) الموجبة (∞)  او السالبة (-∞) .

- مثال (3) : جد النهاية الآتية بيانياً: $\underset{x\to 0}{lim}\frac{1}{x^2}$

الإجابة:

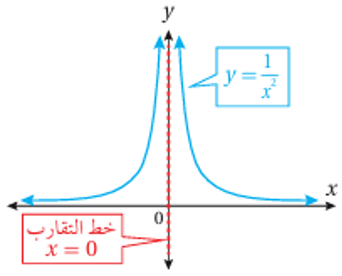نلاحظ من التمثيل البياني للاقتران ، أنه كلما اقتربت قيم x من العدد (0) من جهة اليسار ازدادت قيم f(x) المقابلة لها بصورة غير محدودة ، وهذا يعني أن النهاية عندما تقترب x من العدد (0) من جهة اليسار غير موجودة ، ونلاحظ أيضاً أنه كلما اقتربت قيم x من العدد (0) من جهة اليمين ، ازدادت قيم f(x) المقابلة لها بصورة غير محدودة ، وهذا يعني أن النهاية عندما تقترب x من العدد (0) من جهة اليمين غير موجودة ، يمكن وصف سلوك الاقتران كالآتي :  $\underset{x\to 0^{-}}{lim}\frac{1}{x^2}=\infty , \underset{x\to 0^{+}}{lim}\frac{1}{x^2}=\infty \Rightarrow \underset{x\to 0}{lim}\frac{1}{x^2}=\infty$

---

- تدريب: جد النهاية الآتية بيانياً: $\underset{x\to 2}{lim}\frac{1}{x-2}$

---

إيجاد النهايات جبرياً:  نهاية الاقتران الثابت عند أي نقطة c هي القيمة الثابتة للاقتران. $\underset{x\to c}{lim}k=k$ نهاية الاقتران المحايد : نهاية الاقتران f(x)=x عند النقطة c هي: c $\underset{x\to c}{lim}x=c$

---

الخصائص الأساسية لإيجاد النهايات جبرياً:  اذا كان k,c عددين حقيقيين ، و n عدداً صحيحاً موجباً ، وكانت النهايتان $\underset{x\to c}{lim}f\left(x\right) , \underset{x\to c}{lim}g\left(x\right)$$$ موجودتين ، فإن كلاً من الخصائص الآتية صحيحة:

1) خاصية المجموع: $\underset{x\to c}{lim}\left(f\right(x)+g(x\left)\right)=\underset{x\to c}{lim}f\left(x\right)+\underset{x\to c}{lim}g\left(x\right)$

2) خاصية الفرق:  $\underset{x\to c}{lim}\left(f\right(x)-g(x\left)\right)=\underset{x\to c}{lim}f\left(x\right)-\underset{x\to c}{lim}g\left(x\right)$

3) خاصية الضرب في ثابت:  $\underset{x\to c}{lim}\left(kf\right(x\left)\right)=k\underset{x\to c}{lim}f\left(x\right)$

4) خاصية الضرب:  $\underset{x\to c}{lim}\left(f\right(x)\times g(x\left)\right)=\underset{x\to c}{lim}f\left(x\right)\times \underset{x\to c}{lim}g\left(x\right)$

5) خاصية القسمة:  $\underset{x\to c}{lim}\left(\frac{f\left(x\right)}{g\left(x\right)}\right)=\frac{\underset{x\to c}{lim}f\left(x\right)}{\underset{x\to c}{lim}g\left(x\right)} , \underset{x\to c}{lim}g\left(x\right)\ne 0$

6) خاصية القوة:  $\underset{x\to c}{lim}{\left(f\right(x\left)\right)}^n={(\underset{x\to c}{lim}f\left(x\right) )}^n$

7) خاصية الجذر النوني:  $\underset{x\to c}{lim}\sqrt[n]{f\left(x\right)}=\sqrt[n]{\underset{x\to c}{lim}f\left(x\right) }$

---

- مثال (4) : أستعمل خصائص النهايات لحساب كل نهاية مما يأتي 
1) $\underset{x\to -1}{lim}(x^3-4x+6)$                 2)  $\underset{x\to 4}{lim}\frac{\sqrt{1+3x^2}}{3x-2}$

الإجابة:

2)  $$\begin{gathered} =\frac{\underset{x\to 4}{lim}\sqrt{1+3x^2}}{\underset{x\to 4}{lim}(3x-2)}=\frac{\sqrt{\underset{x\to 4}{lim}(1+3x^2)}}{\underset{x\to 4}{lim}(3x-2)} \\ =\frac{\sqrt{\underset{x\to 4}{lim}1+3{\left(\underset{x\to 4}{lim}x\right)}^2}}{\underset{x\to 4}{lim}3x-\underset{x\to 4}{lim}2}=\frac{\sqrt{49}}{10}=\frac{7}{10} \end{gathered}$$

1)  $$\begin{gathered} \underset{x\to -1}{lim}{x}^3-\underset{x\to -1}{lim}4x+\underset{x\to -1}{lim}6= \\ {\left(\underset{x\to -1}{lim}x\right)}^3-\underset{x\to -1}{lim}4x+\underset{x\to -1}{lim}6= \\ =(-1{)}^3-4(-1)+6=9 \end{gathered}$$

---

- تدريب : أستعمل خصائص النهايات لحساب كل نهاية مما يأتي : 

1) $\underset{x\to 1}{lim}(2x^3+3x^2-4)$               2) $\underset{x\to 5}{lim}\sqrt{\frac{x^2}{x-1}}$

---

النهايات بالتعويض المباشر : 
نهايات كثيرات الحدود : اذا كان f(x) كثير حدود ، وكان c عدداً حقيقياً ، فإن : 
نهايات كثيرات الحدود: اذا كان f(x) كثير حدود ، وكان c عدداً حقيقياً ، فإن: $\underset{x\to c}{lim}f\left(x\right)=f\left(c\right)$

نهايات الاقترانات النسبية: اذا كان $f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)}$ اقتراناً نسبياً ، وكان c عدداً حقيقياً ، فإن:

$\underset{x\to c}{lim}f\left(x\right)=f\left(c\right)=\frac{p\left(c\right)}{q\left(c\right)} ,q\left(c\right)\ne 0$

---

- مثال (5): جد كل نهاية مما يأتي باستعمال التعويض المباشر إذا كان ممكناً ، وإلا فأذكر السبب : 

1) $\underset{x\to 2}{lim}(3x^2-5x+4)$          2) $\underset{x\to -1}{lim}\frac{x^2+5x}{x^4+2}$           3) $\underset{x\to 4}{lim}\frac{x^2-16}{x-4}$

الإجابة:

3) بما أن x=4 لا تقع في مجال الاقتران النسبي (المقام يساوي صفراً عندها) اذن ، لا يمكن إيجاد النهاية بالتعويض المباشر .

2)  $=\frac{{(-1)}^2+5(-1)}{{(-1)}^4+2}=-\frac{4}{3}$

1)  $$\begin{gathered} =3\left(4\right)-5\left(2\right)+4 \\ =12-10+4=6 \end{gathered}$$

---

- تدريب : جد كل نهاية مما يأتي باستعمال التعويض المباشر إذا كان ممكناً ، والا فأذكر السبب : 

1) $\underset{x\to 2}{lim}(x^3-9x+4)$               2) $\underset{x\to 3}{lim}\frac{x^3-5x-6}{x^2-2}$                   3) $\underset{x\to 3}{lim}\frac{x^2-9}{x-3}$

---

في بعض الحالات يكون ناتج (التعويض المباشر $\frac{0}{0}$) ولحل هذه المشكلة نحتاج الى البحث عن صيغة مكافئة للاقتران ، عن طريق تبسيطه جبرياً ، وذلك بتحليل وإيجاد عوامل مشتركة بين كل من البسط والمقام واختصار العوامل المشتركة.

- مثال (6) : جد كل نهاية مما يأتي: 

1) $\underset{x\to -3}{lim}\frac{x^2-x-12}{x+3}$             2) $\underset{x\to 2}{lim}\frac{|x-2|}{x-2}$ 

الإجابة:

1) بما أن ناتج التعويض 0/0  نحلل المقدار جبرياً ونختصر العوامل المشتركة بين البسط والمقام .

$=\underset{x\to -3}{lim}\frac{(x-4)(x+3)}{x+3}=\underset{x\to -3}{lim}(x-4)=-3-4=-7$

2) نعيد تعريف  الاقتران :

$f\left(x\right)=\frac{|x-2|}{x-2}=\left\{\begin{array}{l}\frac{x-2}{x-2} ,x>2\\ -\frac{(x-2)}{x-2},x<2\end{array}\right.$

$$\begin{gathered} \underset{x\to 2^{-}}{lim}f\left(x\right)=\underset{x\to 2^{-}}{lim}(-1)=-1 \\ \underset{x\to 2^{+}}{lim}f\left(x\right)=\underset{x\to 2^{+}}{lim}\left(1\right)=1 \end{gathered}$$

- بما أن النهايتين من اليمين ومن اليسار غير متساويتين ، فإن النهاية غير موجودة .

---

- تدريب : جد كل نهاية مما يأتي: 

1) $\underset{x\to 0}{lim}\frac{7x-x^2}{x}$           2) $\underset{x\to 0}{lim}\frac{2-\sqrt{x+4}}{x}$

---

• الاتصال: 
يكون الاقتران متصلاً ، إذا لم يكن تمثيله البياني أي انقطاع أو قفزة أو فجوة 
ويكون الاقتران متصلاً عند نقطة إذا كان منحناه يمر عبر هذه النقطة دون انقطاع .

• حالات الاتصال أو عدم الاتصال: 

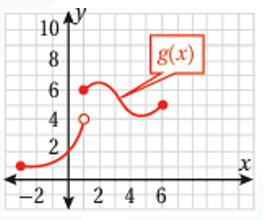
غير متصل عند x=1 لأن الاقتران غير معرف عند x=1	غير متصل عند x=1 بسبب وجود قفزة (ما يعني أن النهاية غير موجودة)
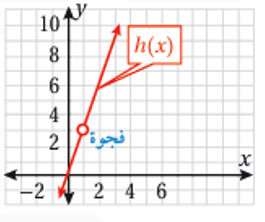
غير متصل عند x=1 لأن الاقتران غير معرف عند x=1 على الرغم أن النهاية موجودة عندما x=1	متصل عند x=1

---

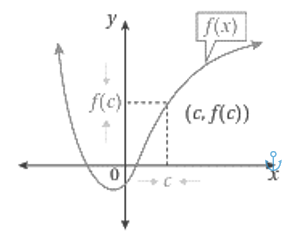
• الاتصال عند نقطة:  يكون الاقتران f(x) متصلاً عند النقطة x=c إذا حقق الشروط الآتية جميعها : - f(x) معرف عند c. - $\underset{x\to c}{\lim }f\left(x\right)$ موجودة. - $\underset{x\to c}{\lim }f\left(x\right)=f\left(c\right)$

- مثال (7): حدد إذا كان كل اقتران مما يأتي متصلاً عند قيمة x المعطاة ، مبرراً أجابتك :

1) $h\left(x\right)=\left\{\begin{array}{l}{x}^2-3 ,x\le -1\\ x-1 ,x>-1\end{array}\right.$               2) $f\left(x\right)=x^3-x , x=3$

الإجابة:

1) نطبق الشروط: 

$h(-1)=(-1{)}^2-3=-2$

$\underset{x\to -1^{-}}{\lim }(x^2-3)=-2$

$\underset{x\to -1^{+}}{\lim }(x-1)=-2$

بما أنّ: $\underset{x\to -1^{-}}{\lim }h\left(x\right)=\underset{x\to -1^{+}}{\lim }h\left(x\right)=-2$

وبما أنّ: $\underset{x\to -1}{\lim }h\left(x\right)=h(-1)=-2$ ، إذن: $h\left(x\right)$ متصل عند $x=-1$
 

2) $f\left(3\right)=(3{)}^3-3=24$

     $\underset{x\to 3}{\lim }f\left(x\right)={\left(3\right)}^2-3=24$

بما أن $\underset{x\to 3}{\lim }f\left(x\right)=f\left(3\right)=24$ ، اذن : f(x) متصل عند x=3

---

- تدريب: حدد إذا كان كل اقتران مما يأتي متصلاً عند قيمة x المعطاة ، مبرراً أجابتك :

1) $h\left(x\right)=\{\begin{array}{l}x-1 ,x<3\\ 5-x ,x\ge 3\end{array}$                   2) $f\left(x\right)=x^5+2x^3-x , x=1$