القيم القصوى والتقعر

                    

إذا كان الاقتران f معرفاً على مجاله D، وكان c عدداً ينتمي إلى مجال الاقتران f:

يقال أن f(c) أنها قيمة عظمى مطلقة للاقتران f إذا كانت $f\left(c\right) \ge f\left(x\right)$ لجميع قيم x في المجال D.

أي أن f(c) أكبر من أو تساوي جميع صور قيم x في المجال D.

يقال أن f(c) أنها قيمة صغرى مطلقة للاقتران f إذا كانت $f\left(c\right) \le f\left(x\right)$ لجميع قيم x في المجال .

أي أن f(c) أصغر من أو تساوي جميع صور قيم x في المجال D.

يطلق على كل من القيم العظمى المطلقة والقيم الصغرى المطلقة القيم القصوى المطلقة.

                  

إذا كانت C نقطة داخلية في مجال الاقتران f:

 يقال أن f(c) أنها قيمة عظمى محلية للاقتران f إذا كان $f\left(c\right)> f\left(x\right)$ لجميع قيم x في فترة مفتوحة تحوي c وتقع داخل المجال.

أي أن f(c) أكبر من جميع صور x المجاورة لِc في مجال f

يقال أن f(c) أنها قيمة صغرى محلية للاقتران f إذا كان $f\left(x\right) > f\left(c\right)$لجميع قيم x في فترة مفتوحة تحوي c وتقع داخل المجال.

أي أن f(c) أصغر من جميع صور x المجاورة لِ c في مجال f.

يطلق على كل من القيم العظمى المحلية والقيم الصغرى المحلية القيم القصوى المحلية.

---

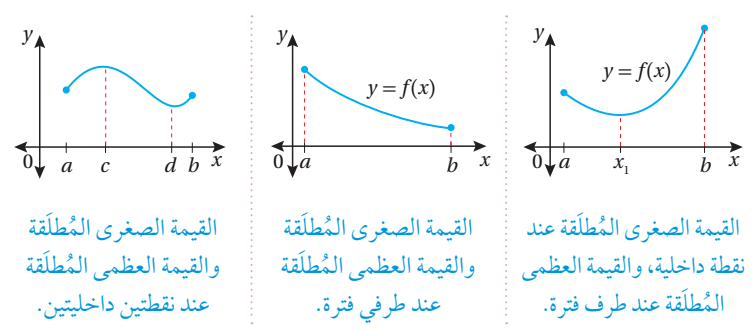
نلاحظ أنه إذا كان الاقتران f معرفاً على الفترة [a, b]:

1. أطراف الفترة المغلقة لا تكون قيماً قصوى محلية ابداً، ويمكن أن تكون قيماً قصوى مطلقة.

2. نقط القيم القصوى المحلية تكون داخل الفترة (a, b) 

3. نقط القيم القصوى المطلقة يمكن أن تكون داخل الفترة (a, b)

4. إذا كان f متصلاً على الفترة [a, b]، فإنه يجب أن تكون للاقتران f قيمة عظمى مطلقة وقيمة صغرى مطلقة في هذه الفترة.

نقول عن النقطة الداخلية $(c, f(c\left)\right)$أنها نقطة حرجة للاقتران f إذا كانت $f^{\text{'}}\left(c\right) = 0$ أو $f^{\text{'}}\left(c\right)$ غير موجودة.

نلاحظ أن من شروط النقطة الحرجة أن تكون نقطة داخلية في مجال الاقتران f وليست طرفاً لفترة المجال.

---

   مثال:

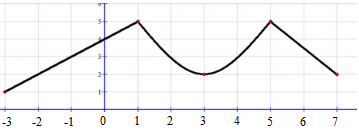
   الشكل المجاور يمثل منحنى الاقتران f المعرّف على الفترة [3,7-] 

1. حدد النقط الحرجة للاقتران f 

 

الحل:

النقط الحرجة:  

(1,5) لأن $f^{\text{'}}\left(1\right)$ غير موجودة( زاوية)

(3,2) لأن $f^{\text{'}}\left(3\right) = 0$(مماس أفقي)

(5,3) لأن $f^{\text{'}}\left(5\right)$ غير موجودة (زاوية)

---

2. جد القيم القصوى المطلقة وبين نوعها:

الحل:

القيمة العظمى المطلقة = 5 = f(1)

القيمة الصغرى المطلقة = 1 =  f(-3)

3 . جد القيم القصوى المحلية وبين نوعها:

الحل:

القيم العظمى المحلية = 5 = f(1)

القيم الصغرى المحلية = 2 = f(3)

نلاحظ أن: 

النقطة (3,1-) نقطة قيمة صغرى مطلقة، ولكنها ليست محلية( لأنها ليست نقطة داخلية).

النقطة (1,5) نقطة قيمة عظمى محلية ومطلقة.

النقطة (5,3) نقطة حرجة، لكنها ليست نقطة قيمة قصوى.

النقطة (7,4) ليست نقطة حرجة وليست نقطة قيمة قصوى.

---

                    

لإيجاد القيم القصوى المطلقة للاقتران f المتصل على الفترة المغلقة [a, b] نتبع الخطوات التالية:

الخطوة 1: نجد قيم f عند قيم x الحرجة في الفترة المفتوحة (a, b) 

الخطوة 2: نجد قيم f(a) و f(b).

الخطوة 3: اتخاذ القرار

القيمة العظمى المطلقة = أكبر القيم الناتجة في الخطوة 1 و 2

القيمة الصغرى المطلقة = أصغر القيم الناتجة في الخطوة 1 و 2

ولإيجاد القيم القصوى للاقتران $f\left(x\right) = x^3-3x$ المعرّف على الفترة [2,4-] والمتصل عليها: 

                     $$\begin{gathered} Solution: \\ f^{\text{'}}\left(x\right) = 3x^2-3 = 0 \\ 3x^2-3 = 0 \\ {x}^2-1 = 0 \\ {x}^2= 1 \\ x = 1, x = -1 \end{gathered}$$            

الخطوة 1: قيم x الحرجة للاقتران f هي x=1,-1 

 

                    $$\begin{gathered} f(-1) = 2 \\ f\left(1\right) = -2 \end{gathered}$$

الخطوة 2:

  $$\begin{gathered} f(-2) =-2 \\ f\left(4\right) = 52 \end{gathered}$$

3. القيمة العظمى المطلقة هي: $f\left(4\right)=52$

القيمة الصغرى المطلقة هي:  $f\left(1\right) = f(-2)=-2$

---

يمكن إيجاد القيم القصوى المحلية للاقتران f المتصل على الفترة [a, b] عن طريق اتباع الخطوات التالية:

1) إيجاد القيم الحرجة للاقتران f على الفترة (a , b)

2) البحث في إشارة المشتقة الأولى $f^{\text{'}}$ على الفترة (a , b)

3) دراسة تزايد وتناقص الاقتران f،

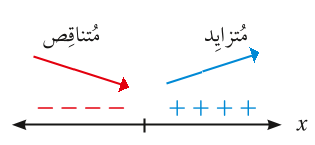    بحيث يكون الاقتران f متزايداً في الفترة التي تكون فيها $f^{\text{'}}$ موجبة .

    و يكون الاقتران f متناقصاً في الفترة التي تكون فيها $f^{\text{'}}$ سالبة.

 

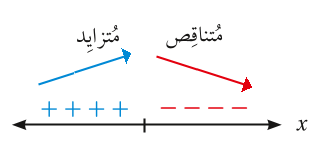      يكون للاقتران f قيمة عظمى محلية عند نقطة تحول الاقتران f من تزايد إلى تناقص

      ( أي تحول إشارة المشتقة الأولى من موجبة إلى سالبة).

   

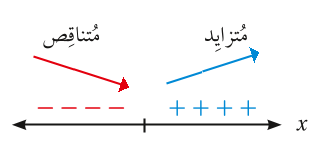      ويكون للاقتران f قيمة صغرى محلية عند نقطة تحول الاقتران f من تناقص إلى تزايد

      (أي تحول إشارة المشتقة الأولى من سالبة إلى موجبة)

 

ملاحظات حول القيم القصوى المحلية والمطلقة:

1) يمكن أن يوجد للاقتران المتصل f أكثر من نقطة قيمة عظمى (أو صغرى) مطلقة، تتساوى جميعها في الإحداثي y، فمثلاً:

     

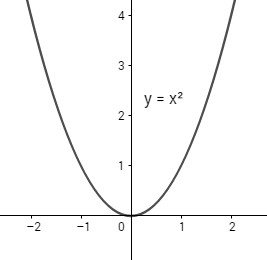
     الاقتران$f\left(x\right) = x^2$ المعرف على الفترة [2,2-]، والممثل جانباً: 

     له قيمة عظمى مطلقة عند x=2 و x=-2

      وقيمها f(2) = f(-2) = 4

 

 

2) الاقتران الثابت، مثل الاقتران $g\left(x\right) = 5$ ، حيث x تنتمي إلى الفترة [0,5]

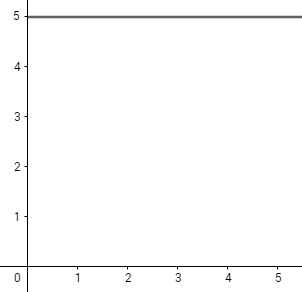  لكل c في الفترة [0,5], فإن $g\left(c\right) = 5$

  يمكن اعتبار g(c) = 5 قيمة عظمى مطلقة، لأن $g\left(c\right) = 5\ge g\left(x\right)$ لجميع قيم x في الفترة [0,5].

  يمكن اعتبار g(c) = 5 قيمة صغرى مطلقة، لأن $g\left(c\right) = 5\le g\left(x\right)$ لجميع قيم x في الفترة [0,5].

   لا يوجد للاقتران g قيم قصوى محلية، لأن g(c) = 5 لا يمكن أن تكون أكبر من ( أصغر من) g(x)

   لجميع قيم x في فترة مفتوحة تحوي c وتقع كاملة ضمن الفترة (0,5).

 

 

                  

إذا كان الاقتران f قابلاً للاشتقاق على الفترة المفتوحة L:

1- نقول عن الاقتران f أنه مقعر للأعلى على الفترة L، إذا كان منحنى الاقتران f يقع فوق جميع مماساته على الفترة،

   وفي هذه الحالة، يكون: $f^{\text{'}}$ متزايدة، (ميل مماساته يتزايد)

   وكذلك  $f^{\text{'}\text{'}}>0$ (اشارة المشتقة الثانية موجبة)

2- نقول عن الاقتران f أنه مقعر للأسفل على الفترة L، إذا كان منحنى الاقتران f يقع تحت جميع مماساته على الفترة،

   وفي هذه الحالة، يكون: $f^{\text{'}}$متناقصة (ميل مماساته يتناقص)

   وكذلك $f^{\text{'}\text{'}}<0$ (إشارة المشتقة الثانية سالبة)

3- نقول عن النقطة $(c, f(c\left)\right)$ أنها نقطة انعطاف للاقتران f إذا غيّر الاقتران f من تقعره حول هذه النقطة،

    بشرط أن يكون لمنحنى الاقتران f مماس وحيد عندها.

   (أي إما أن تكون $f^{\text{'}}\left(c\right)$ موجودة كعدد حقيقي فيكون لمنحنى f مماس عندها، أو أن يكون له مماس رأسي عندها)

نلاحظ أنه عند نقطة الانعطاف $(c, f(c\left)\right)$ اما ان تكون $f^{\text{'}\text{'}}\left(c\right) = 0$ أو $f^{\text{'}\text{'}}\left(c\right)$ غير موجودة.

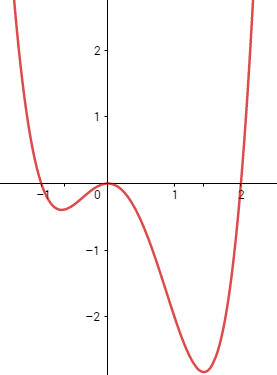  فمثلاً:

  في الشكل المجاور الذي يمثل منحنى الاقتران fالمعرف على R:

   1. منحنى الاقتران f مقعر للأعلى على الفترتين:$(-\infty ,-\frac{1}{2}) , (\frac{3}{2},\infty )$

   2. منحنى الاقتران f مقعر للأسفل على الفترة: $(-\frac{1}{2},\frac{3}{2})$

   3. الاقتران f له نقطتا انعطاف عند كل من  $x=-\frac{1}{2} و x= \frac{3}{2}$

  4 . نلاحظ أنه f له مماس وحيد عند كل من $x=-\frac{1}{2} و x= \frac{3}{2}$.

---

                  

يمكن تحديد نوع القيمة القصوى المحلية باستخدام إشارة المشتقة الثانية، بشرط أن تكون c نقطة داخلية في مجال الاقتران $f^{\text{'}\text{'}}, f^{\text{'}}, f$ موجودتان في فترة مفتوحة تحتوي c، $f^{\text{'}}\left(c\right) = 0$

إذا كان $f^{\text{'}\text{'}}\left(c\right) < 0$، فإن f(c) تكون قيمة عظمى محلية للاقتران f.

إذا كان $f^{\text{'}\text{'}}\left(c\right) > 0$، فإن f(c) تكون قيمة صغرى محلية للاقتران f. 

إذا كان $f^{\text{'}\text{'}}\left(c\right) = 0$، فإن هذا الاختبار يفشل، ونعود لاستخدام اختبار المشتقة الأولى الذي يعتمد على تزايد وتناقص الاقتران f.

---

يمكن تطبيق مفاهيم القيم القصوى والتزايد والتناقص في مجالات حياتية كثيرة، من أهمها اقتران الموقع(s) والسرعة (v) والتسارع (a)، اعتماداً على أن:

السرعة (v) هي المشتقة الأولى لاقتران الموقع (s) بالنسبة إلى الزمن. 

$v\left(t\right) = s^{\text{'}}\left(t\right)$

والتسارع هو المشتقة الأولى لاقتران السرعة (v)، والمشتقة الثانية لاقتران الموقع (s) بالنسبة إلى الزمن.

$a\left(t\right) = v^{\text{'}}\left(t\right) = s^{\text{'}\text{'}}\left(t\right)$