التحويلاتُ الهندسيَّةُ للاقترانِ التربيعيِّ
Transformations of Quadratic Function
فكرةُ الدرسِ : تمثيلُ مُنحنياتِ الاقتراناتِ التربيعيَّةِ الناتجةِ عنْ تطبيقِ تحويلٍ هندسيٍّ أوْ أكثرَ على مُنحنى الاقتران الرئيس.
أولًا : الانسحابُ
|
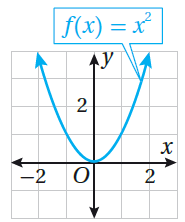
تعلمتُ سابقًا أن الاقتران الرئيس لعائلة الاقترانات التربيعية هو
، الذي يأخذُ مُنحناهُ شكل القطع المُكافئ، كما في الشكل المُجاور. |
 |
أما مُنحنياتُ الاقترانات التربيعية الأُخرى فهي ناتجة عن تطبيق تحويل هندسي أو أكثر على مُنحنى الاقتران الرئيس، بحيثُ تغيرُ هذه التحويلاتُ
الهندسيةُ موقع الاقتران الرئيس أو أبعادهُ.
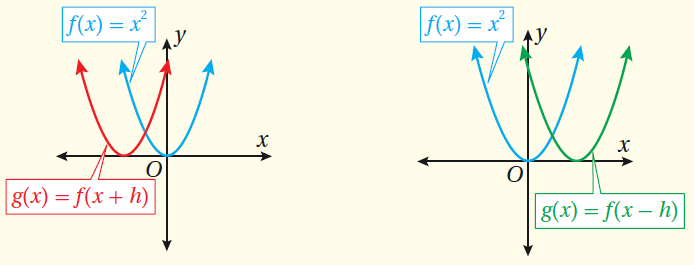
يُعد الانسحابُ أحد التحويلات الهندسية التي تؤثرُ في موقع الاقتران الرئيس وتنقُلُهُ إما إلى الأعلى أو إلى الأسفل أو إلى اليمين أو إلى اليسار دون تغيير في أبعاده.
الانسحاب الرأسي
عند إضافة الثابت الموجب إلى قاعدة الاقتران الرئيس أو طرحه منها فإن مُنحنى الاقتران هُو مُنحنى الاقتران الرئيس مُزاحًا
إلى الأعلى أو إلى الأسفل بمقدار وحدةً، ويُسمى هذا التحويلُ الانسحاب الرأسي.
|
مفهومٌ أساسيٌّ (الانسحابُ الرأسيُّ للاقترانِ التربيعيِّ) إذا كان وكان k عددًا حقيقيًّا موجبًا، فإنَّ: • مُنحنى ، هو مُنحنى (f(x مُزاحًا إلى الأعلى k وحدة. • مُنحنى ، هو مُنحنى (f(x مُزاحًا إلى الأسفل k وحدة.
|
مثال
أصفُ كيف يرتبطُ مُنحنى كل اقتران مما يأتي بمُنحنى الاقتران الرئيس ، ثم أُمثلُهُ بيانيا :
الحل :
|
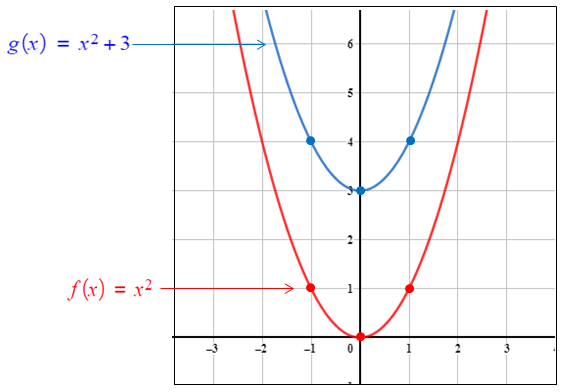
منحنى هو منحنى مُزاحًا 3 وحدات إلى الأعلى لتمثيل مُنحنى بيانيًا أتبعُ الإجراءات الآتية : • أختارُ مجموعةً من النقاط التي تقعُ على مُنحنى • أُضيفُ 3 للإحداثي y للنقاط التي اخترتُها. • أُمثلُ النقاط الجديدة في المُستوى الإحداثي، ثم أصلُ بينها بمُنحنًى أملس، كما يظهرُ في الشكل المُجاور. |
 |
|
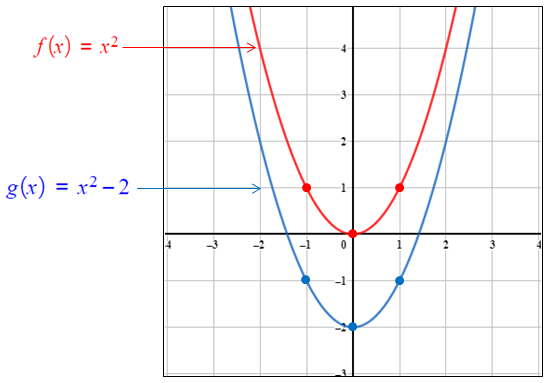
منحنى هو منحنى مُزاحًا وحدتين إلى الأسفل لتمثيل مُنحنى بيانيًا أتبعُ الإجراءات الآتية : • أختارُ مجموعةً من النقاط التي تقعُ على مُنحنى • أطرح 2 من الإحداثي y للنقاط التي اخترتها • أُمثلُ النقاط الجديدة في المُستوى الإحداثي، ثم أصلُ بينها بمُنحنًى أملس، كما يظهرُ في الشكل المُجاور.
|
 |
|
•• أتعلمُ : عند اختيار مجموعة من النقاط على مُنحنى الاقتران الرئيس يُفضلُ أن تتوسط نقطةُ الرأس هذه النقاط. فمثلاً، يمكنُ اختيارُ النقاط الآتية : (1 , 1-) , (4 , 2-) , (0 , 0), (1 , 1), (4 , 2) |
الانسحابَ الأفقيَّ
عند إضافة الثابت الموجب إلى قيم جميعها في مجال الاقتران أو طرحه منها، فإن مُنحنى الاقتران هُو مُنحنى الاقتران
الرئيس مُزاحًا إلى اليمين أو إلى اليسار بمقدار وحدةً، ويُسمى هذا التحويلُ الانسحاب الأفقي.
|
مفهومٌ أساسيٌّ (الانسحابُ الأفقيُّ للاقترانِ التربيعيِّ) إذا كان وكان h عددًا حقيقيًّا موجبًا، فإنَّ : • مُنحنى ، هُوَ مُنحنى مُزاحًا إلى اليمينِ h وحدةً. • مُنحنى ، هُوَ مُنحنى مُزاحًا إلى اليسار h وحدةً.
|
مثال
أصفُ كيف يرتبطُ مُنحنى كل اقتران مما يأتي بمُنحنى الاقتران الرئيس ، ثم أُمثلُهُ بيانيا :
الحل :
|
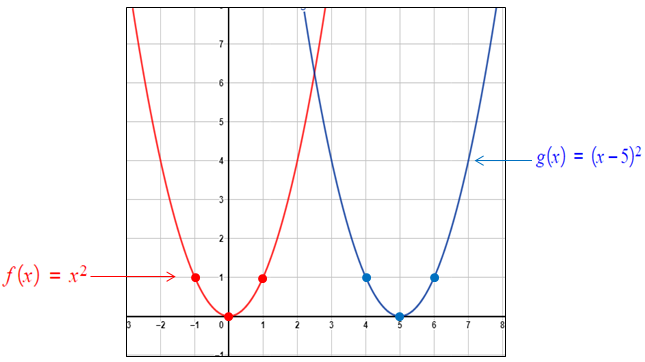
منحنى هو منحنى مُزاحًا 5 وحدات إلى اليمين لتمثيل مُنحنى بيانيًا أتبعُ الإجراءات الآتية : • أختارُ مجموعةً من النقاط التي تقعُ على مُنحنى • أضيف 5 إلى الإحداثي x للنقاط التي اخترتها • أُمثلُ النقاط الجديدة في المُستوى الإحداثي، ثم أصلُ بينها بمُنحنًى أملس، كما يظهرُ في الشكل المُجاور. |
 |
|
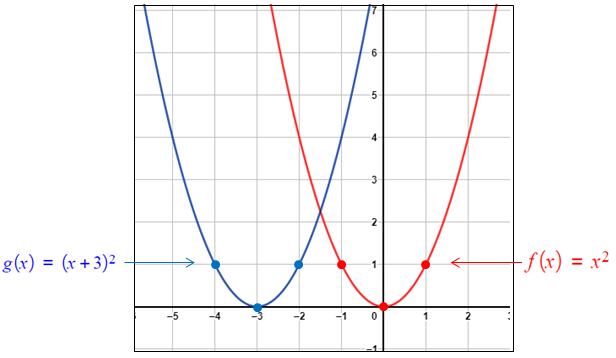
منحنى هو منحنى مُزاحًا 3 وحدات إلى اليسار لتمثيل مُنحنى بيانيًا أتبعُ الإجراءات الآتية : • أختارُ مجموعةً من النقاط التي تقعُ على مُنحنى • أطرح 3 من الإحداثي x للنقاط التي اخترتها • أُمثلُ النقاط الجديدة في المُستوى الإحداثي، ثم أصلُ بينها بمُنحنًى أملس، كما يظهرُ في الشكل المُجاور.
|
 |
ثانيًا : التمدُّدُ
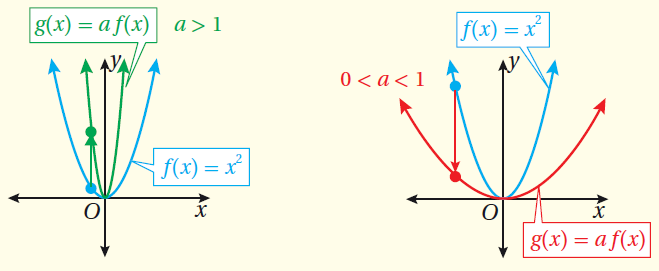
التمدُّدُ : هُوَ تحويلٌ هندسيٌّ يؤدّي إلى توسيعِ مُنحنى الاقترانِ أوْ تضييقِهِ، فعندَ ضربِ الاقترانِ الرئيسِ (f(x بالثابتِ a ؛ حيثُ a عددٌ حقيقيٌّ موجِبٌ، فإنَّ مُنحنى الاقترانِ a f(x) هُوَ توسيعٌ أوْ تضييقٌ رأسيٌّ لِمُنحنى الاقترانِ f(x).
|
مفهومٌ أساسيٌّ (تمددُ الاقترانِ التربيعيِّ) إذا كان وكان a عددًا حقيقيًّا موجبًا، فإنَّ مُنحنى هو : • توسيع رأسي بمعاملٍ مقدارُهُ a لِمُنحنى (f(x ، إذا كانتْ a > 1 • تضييق رأسي بمعاملٍ مقدارُهُ a لِمُنحنى (f(x ، إذا كانتْ
|
مثال
أصفُ كيف يرتبطُ مُنحنى كل اقتران مما يأتي بمُنحنى الاقتران الرئيس ، ثم أُمثلُهُ بيانيا :
|
مُنحنى (g(x هو توسيع رأسيٌّ لمُنحنى بمعامل مقدارهُ 3 لتمثيل مُنحنى (g(x بيانيًّا أتَّبع الإجراءات الآتية : • أختار مجموعة من النقاط تقع على مُنحنى • · أضرب الإحداثيَّ y للنقاط التي اخترتُها في 3 • · أُمثل النقاط الجديدة في المُستوى الإحداثيِّ، ثمَّ أصِلُ بينها بمُنحنًى أملَس، كما يظهَرُ في الشكل المُجاور. |
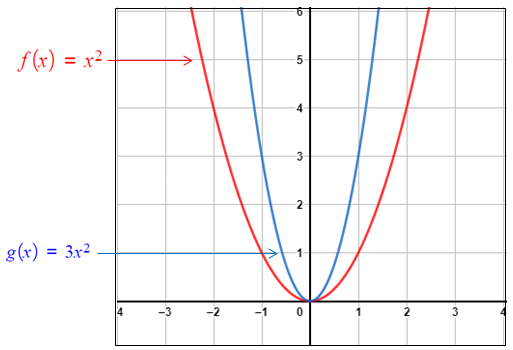 |
| •• أتعلَّمُ : ألاحظُ أنَّ منحنى الاقترانِ التربيعيِّ عندَما يتوسَّعُ رأسيًّا، فإنّهُ يبدو أضيقَ أفقيًّا منَ الاقترانِ الرئيسِ. |
|
مُنحنى (g(x هو تضييق رأسيٌّ لمُنحنى لتمثيل مُنحنى (g(x بيانيًّا أتَّبع الإجراءات الآتية : • أختار مجموعة من النقاط تقع على مُنحنى • · أضرب الإحداثيَّ y للنقاط التي اخترتُها في • · أُمثل النقاط الجديدة في المُستوى الإحداثيِّ، ثمَّ أصِلُ بينها بمُنحنًى أملَس، كما يظهَرُ في الشكل المُجاور. |
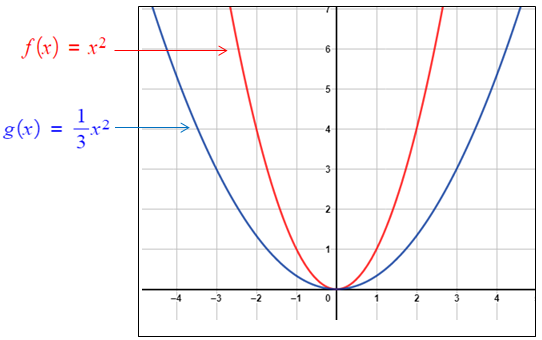 |
| •• أتعلَّمُ : ألاحظُ أنَّ منحنى الاقترانِ التربيعيِّ عندَما يضيقُ رأسيًّا، فإنّهُ يبدو أوسعَ أفقيًّا منَ الاقترانِ الرئيسِ. |
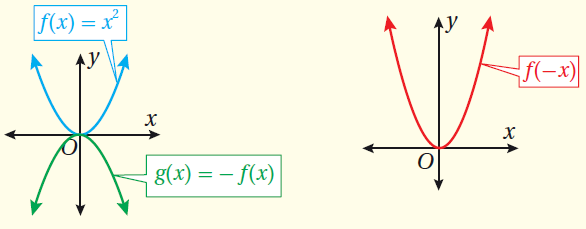
ثالثًا : الانعكاسُ
الانعكاسُ : هُوَ تحويلٌ هندسيٌّ يعكِسُ مُنحنى الاقترانِ حولَ مُستقيمٍ مُحَدَّدٍ.
|
مفهومٌ أساسيٌّ (الانعكاسُ) إذا كان فإنَّ : • مُنحنى ، هُوَ انعكاسٌ لِمُنحنىحولَ المحورِ x • مُنحنى ، هُوَ انعكاسٌ لِمُنحنى حولَ المحورِ y
|
| •• أتعلَّمُ : انعكاسُ الاقترانِ حولَ المحورِ y يُعطي الاقترانَ نفسَهُ ؛ لأنَّ : |
مثال
أصفُ كيف يرتبطُ مُنحنى كل اقتران مما يأتي بمُنحنى الاقتران الرئيس ، ثم أُمثلُهُ بيانيا :
|
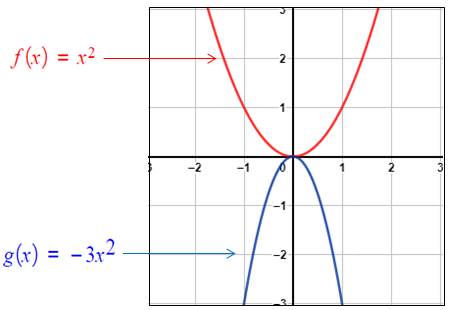
مُنحنى (g(x هُوَ انعكاسٌ لِمُنحنى حولَ المحورِ x، ثمَّ توسيعٌ رأسيٌّ بِمِعاملٍ مقدارُهُ 3 لتمثيلِ مُنحنى (g(x بيانيًّا أتَّبِعُ الإجراءاتِ الآتيةَ : • أختارُ مجموعةً مِنَ النقاطِ تقعُ على مُنحنى • أضربُ الإحداثِيَّ y للنقاطِ التي اخترتُها في 3 - • أُمَثِّلُ النقاطَ الجديدةَ في المُستوى الإحداثِيِّ، ثمَّ أَصِلُ بينها بمُنحنًى أملَسَ، كما يظهرُ في الشكلِ المُجاورِ. |
 |
|
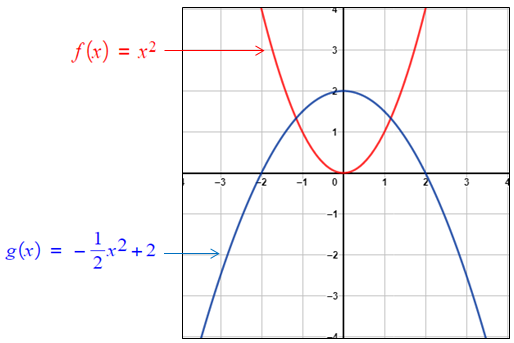
مُنحنى (g(x هُوَ انعكاسٌ لِمُنحنى حولَ المحورِ x، ثمَّ تضييق رأسيٌّ بِمِعاملٍ مقدارُهُ ، ثمَّ انسحابُ وحدتَيْنِ إلى الأعلى. لتمثيلِ مُنحنى (g(x بيانيًّا أتَّبِعُ الإجراءاتِ الآتيةَ : • أختارُ مجموعةً مِنَ النقاطِ تقعُ على مُنحنى • أضربُ الإحداثِيَّ y للنقاطِ التي اخترتُها في • · أُضيفُ 2 إلى الإحداثِيِّ y للنقاطِ الناتجةِ مِنَ الخُطوةِ السابقةِ. • أُمَثِّلُ النقاطَ مِنَ الخُطوةِ السابقةِ في المُستوى الإحداثِيِّ، ثمَّ أَصِلُ بينها بِمُنحنًى أملَسَ، كما يظهَرُ في الشكلِ المُجاورِ. |
 |
رابعًا : كتابةُ التحويلِ الهندسيِّ للاقترانِ التربيعيِّ
تُسَمّى الصيغةُ صيغةَ الرأسِ للاقترانِ التربيعيِّ ؛ حيثُ a ≠ 0 وَ ( h , k ) هُوَ رأسُ القطعِ المُكافِئِ، ويمكنُ استعمالُها لكتابةِ قاعدةِ الاقترانِ التربيعيِّ الناتجِ مِنْ تطبيقِ تحويلٍ هندسيٍّ أوْ أكثرَ على الاقترانِ التربيعيِّ الرئيسِ، بحيثُ يُمَثِّلُ h الانسحابَ الأفقيَّ ، وَيُمَثِّلُ k الانسحابَ الرأسيَّ ، أمّا a فَيُمَثِّلُ الانعكاسَ والتمدُّدَ الرأسيَّ.
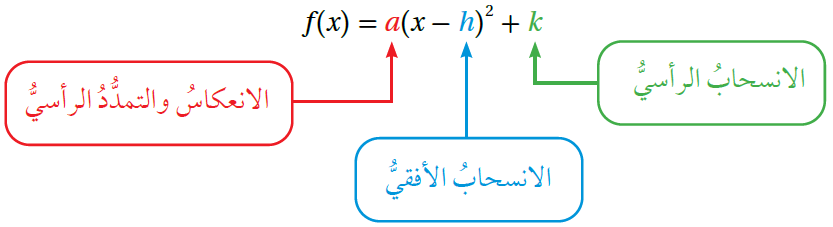
مثال :
إذا كان مُنحنى الاقتران (g(x ناتجًا من انعكاس مُنحنى الاقتران الرئيس حول المحور x، ثمّ توسيع رأسيّ بمعامل مقدارهُ 3، ثمّ
انسحاب إلى اليسار بمقدار وحدتين ، ثمّ انسحاب إلى الأعلى بمقدار 4 وحدات، فأجيب عن الأسئلة الآتية :
1) أكتبُ قاعدةَ الاقترانِ (g(x باستعمالِ صيغةِ الرأسِ.
2) أَجِدُ إحداثيّي رأس القطع، ومُعادلة محور التماثُل، والقيمة العُظمى أو الصُّغرى للاقتران g(x).
3) أُمَثِّلُ الاقترانَ (g(x بيانيًّا.
الحل :
1) أكتبُ قاعدةَ الاقترانِ (g(x باستعمالِ صيغةِ الرأسِ.
• بما أنَّ الانعكاسَ حولَ المحورِ x ، ومعاملَ التوسيعِ الرأسيِّ 3 ، فإنَّ : a = -3
• بما أنَّ الانسحابَ الأفقيَّ إلى اليسارِ بِمِقدارِ 2، فإنَّ : h = -2
• بما أنَّ الانسحابَ الرأسيَّ إلى الأعلى بِمِقدارِ 4 ، فإنَّ : k = 4
| صيغةُ الرأسِ للاقترانِ التربيعيِّ | |
| بتعويض | |
| بالتبسيطِ |
2) أَجِدُ إحداثيّي رأس القطع، ومُعادلة محور التماثُل، والقيمة العُظمى أو الصُّغرى للاقتران g(x).
بما أنَّ ، فإنَّ:
• رأسُ القطعِ ( 4 , 2-)
• مُعادلةُ محورِ التماثلِ x = -2
• القيمةُ العُظمى 4
3) أُمَثِّلُ الاقترانَ (g(x بيانيًّا.
يُمكِنُني استعمالُ التحويلاتِ الهندسيَّةِ لتمثيلِ مُنحنى الاقترانِ، كما في الشكلِ المُجاورِ.
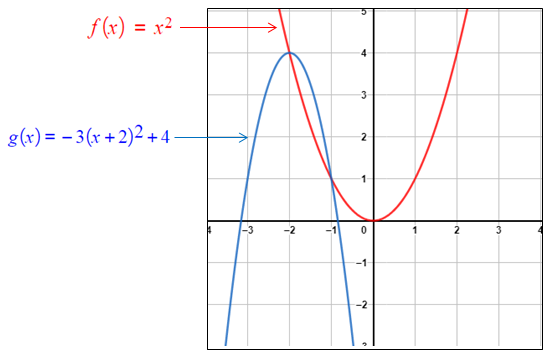
| •• أتعلَّمُ : أستعملُ الإشارةَ السالبةَ للدَّلالةِ على الانعكاسِ حولَ المحورِ ،x والانسحابِ إلى اليسارِ وإلى الأسفلِ. |