الاقتراناتُ

 الاقترانات  

Functions

فكرة الدرس : تَعرُّفُ العلاقة، وتحديدُ ما إذا كانت العلاقةُ اقترانًا أم لا.
                       تحديدُ مجالِ الاقترانِ ومداهُ.

أولًا : العلاقة والاقتران 

تمثِّل أيُّ مجموعة من الأزواج المُرتبة علاقة ؛ حيث الإحداثيُّ x للأزواج المُرتبة هو المُدخلات، والإحداثيّ y هو المُخرجات، ويمكن التعبير عن العلاقة

بطرائق مختلفة ، منها : الأزواج المُرتبة ، والتمثيل البيانيّ ، وجدول المُدخلات والمُخرجات ، والمُخَطَّطُ السهميّ. فمثلاً، تُمثل مجموعة الأزواج

المُرتّبة الآتية علاقة :

                                                                                                                                                                                                                {(1, 6), (-3, 2), (5, 0), (-1, -5), (4, 2)}

ويمكن التعبير عن هذه العلاقة بطرائق مختلفة، كما يأتي:

 

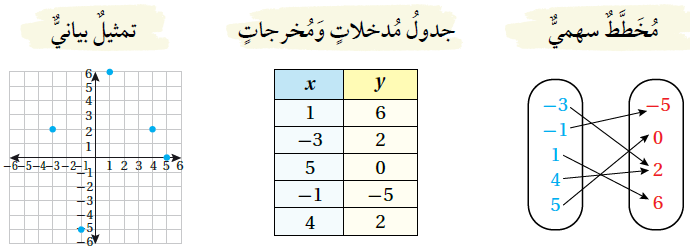
تُسمّى مجموعة مُدخلات العلاقة المجال ، أمّا مجموعة مُخرجات العلاقة فَتُسمّى المدى ، وَتُسَمّى العلاقةُ التي تربطُ كلَّ عنصرٍ في مجالِها

بعنصرٍ واحدٍ فقط من المَدى اقترانًا.  

مثال : 

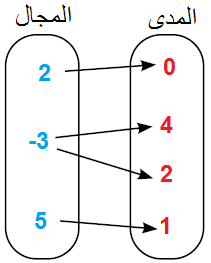
أُحَدِّدُ مجالَ كلِّ علاقة ممّا يأتي وَمَداها، ثمَّ أُحَدِّد ما إذا كانت تمثِّل اقترانًا أم لا : 

1)

الحل : 

المجالُ: { 5 , 3- , 2}

المَدى: { 1 , 2 , 4 , 0}

أُلاحِظُ ارتباطَ العنصر 3- في المجال بالعنصرينِ 4 وَ 2 في المَدى. إذن، لا تمثِّل هذه العلاقة اقترانًا.

 

 

---

 2) 

4	2	0	3-	x
8	6	4	1	y

        

الحل : 

المجالُ: { 4 , 2 , 0 , -3}

المَدى: { 8 , 6 , 4 , 1}

أُلاحِظُ ارتباطَ كلِّ عنصُرٍ في المجالِ بعنصرٍ واحدٍ في المَدى. إذنْ، تمثِّلُ هذهِ العلاقةُ اقترانًا.

---

3) {(0, 0) , (1, 1) , (2, 4) , (-1, 1) ,(-2, 2) } 

 

الحل : 

المجالُ: {2- , 1- , 2 , 1 , 0}

المَدى: { 2 , 4 , 1 , 0}

أُلاحِظُ ارتباطَ كلِّ عنصرٍ في المجالِ بعنصرٍ واحدٍ في المَدى. إذنْ، تمثِّلُ هذهِ العلاقةُ اقترانًا.

•• أتعلَّمُ : يمكنُ أنْ يرتبطَ أكثرُ منْ عنصرٍ في مجالِ الاقترانِ بعنصرٍ واحدٍ في مداهُ.

 

 

---

 

ثانيًا : الاقترانُ المُتَّصِلُ والاقترانُ المُنفَصِلُ

يُسَمّى الاقتران الذي يُمَثّل في المُستوى الإحداثيّ بنقاط غير مُتَّصلة اقترانًا مُنفَصِلًا ، أمّا الاقتران الذي يُمَثّلُ بخطٍّ أو منحنًى دون انقطاعٍ فَيُسمى

اقترانًا مُتّصِلًا .  
 

•• يمكنُ تحديدُ مجال الاقترانات المُنفصلة والمُتّصلة وَمداها من خلال تمثيلِها بيانيًّا، كما في المثال الآتي :

مثال : 

أُحَدّدُ ما إذا كانَ كلُّ اقترانٍ ممّا يأتي مُنفصلًا أمْ مُتَّصلًا ، ثمَّ أُحَدّدُ مجالهُ وَمداهُ :

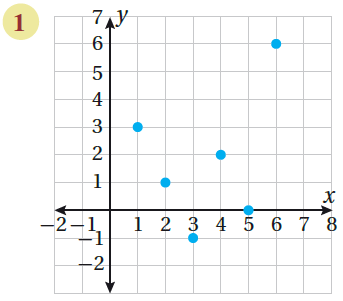
الاقتران المُمَثّل في الشكل المُجاور مُنفَصل؛ لأنَّ تمثيله في المُستوى الإحداثيّ على شكل نقاط غير مُتصلة. لتحديد مجال الاقتران ومداه، أكتب الأزواج المُرتبة وأُحدد منها المجال والمدى. الأزواج المُرتبة : {( 6 , 6) ,( 0 , 5) ,( 2 , 4) ,( 1- , 3) ,( 1 , 2) ,( 3 , 1)} المجال : { 6 , 5 , 4 , 3 , 2 , 1 } المدى: { 6 , 0 , 2 , 1- , 1 , 3}

 

 

 

 

 

 

 

 

---

 

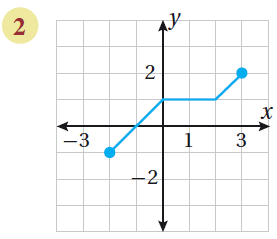
الاقتران المُمثل في الشكل المُجاور مُتّصِلٌ؛ لأنَّ تمثيله في المُستوى الإحداثيّ على شكل قطعٍ مستقيمةٍ دونَ انقطاعٍ.
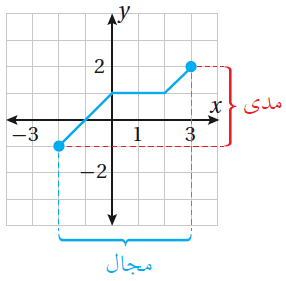
أَستعمِلُ التمثيلَ البيانيَّ لتحديدِ قِيَمِ x وَقِيَمِ y، التي تمثِّلُ المجالَ وَالمَدى كما في الشكل المجاور   المجال : { x | -2 ≤ x ≤ 3 } أوِ الفترةِ [ 3 , 2-]. المَدى : { y | -1 ≤ y ≤ 2 } أوِ الفترةِ [ 2 , 1-].

 

 

 

 

 

 

 

 

 

 

 

 

 

•• أتعلَّمُ :  • يُكتَبُ مجالُ الاقترانِ المُنفَصِلِ وَمَداهُ على شكلِ مجموعةٍ مِنَ العناصرِ المُنفَصِلَةِ. • يُكتَبُ مجالُ الاقترانِ المُتَّصِلِ وَمَداهُ على شكلِ فتراتٍ أوْ مُتبايناتٍ.

 

 

 

 

---

 

الاقترانُ المُمَثَّلُ في الشكلِ المُجاورِ مُتَّصِلٌ؛ لأنَّ تمثيلَهُ في المُستوى الإحداثيِّ على شكلِ منحنًى ليسَ فيهِ انقطاعٌ.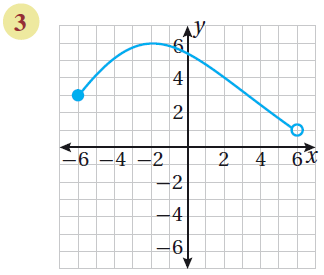
أستعمِلُ التمثيلَ البيانيَّ لتحديدِ قِيَمِ x وَقِيَمِ ،y التي تُمَثِّلُ المجالَ والمَدى كما في الشكل المجاور المجالُ : { x | -6 ≤ x < 6 } أوِ الفترةِ ( 6 , 6-] المَدى : { y | 1< y ≤ 6 } أوِ الفترةِ [ 6 , 1)

 

 

 

 

 

 

 

 

 

 

 

 

 

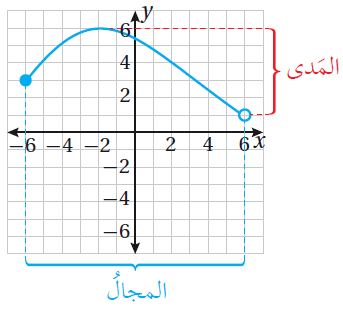•• أتعلَّمُ :  تعني الدائرةُ المفتوحةُ في التمثيلِ البيانيِّ أنَّ الإحداثيَّ x للزوجِ المُرَتَّبِ لا ينتمي إلى مجالِ الاقترانِ، والإحداثيَّ y لا ينتمي إلى مَدى الاقترانِ بسببِ قيمةِ x، وَيُعَبَّرُ عنْ ذلكَ عندَ كتابةِ الفتراتِ باستعمالِ الرمز ) أو الرمز (.

 

 

 

•• اختبارُ الخطِّ الرأسيِّ

يُمكنُني استعمالُ اختبارِ الخطِّ الرأسيِّ لتحديدِ ما إذا كانَتِ العلاقةُ المُمَثَّلَةُ بيانيًّا تُمَثِّلُ اقترانًا أمْ لا.

مفهوم أساسيّ (اختبار الخطِّ الرأسيّ) 

بالكلماتِ : تُعَدُّ العلاقةُ المُمَثَّلَةُ بيانيًّا اقترانًا إذا لم يَقطَعْ أيُّ خطٍّ رأسيٍّ تمثيلَها البيانيَّ في أكثرِ مِنْ نقطةٍ واحدةٍ.

أمثلةٌ :

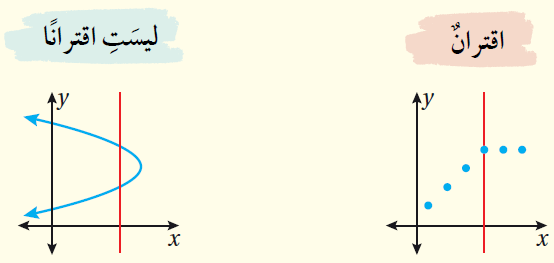
مثال : 

أُحَدِّدُ ما إذا كانت العلاقة المُمَثَّلَة بيانيًّا في كلٍّ ممّا يأتي تُمَثِّل اقترانًا أم لا، مُبَرِّرًا إجابتي:

1)		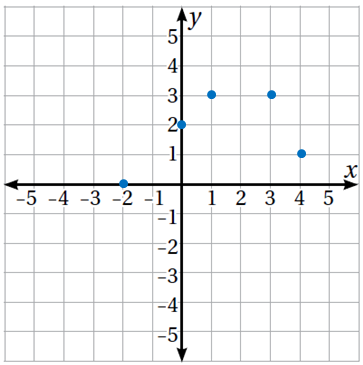تُمَثِّلُ العلاقةُ المُمَثَّلَةُ في الشكلِ المُجاورِ اقترانًا؛ لأنَّهُ لا يوجَدُ خطٌّ رأسيٌّ يَمُرُّ بأكثرَ مِنْ نقطةٍ واحدةٍ في تمثيلِها البيانيِّ.
2)		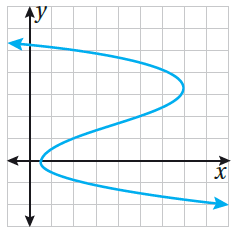لا تُمَثِّلُ العلاقةُ المُعطى تمثيلُها البيانيُّ في الشكلِ المُجاورِ اقترانًا؛ لأنَّها تفشلُ في اختبارِ الخطِّ الرأسيِّ. فمثلًا  ، يوجدُ مستقيمٌ رأسيٌّ يقطعُ التمثيلَ البيانيَّ في ثلاث نقاطٍ عندما x = 2 وهذا يعني أنَّ القيمةَ x = 2 في المجالِ ترتبطُ بثلاثِ قِيَمٍ مختلفةٍ لِـ y في المَدى.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

•• رمزُ الاقترانِ والاقترانُ الخطيُّ

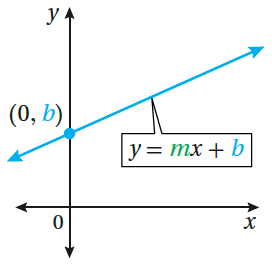
يُبيّن الشكل المُجاور التمثيل البيانيّ لمُعادلة خطيَّة بمتغيّرين، وقَد تعلَّمتُ سابقًا كتابَتَها باستعمال صيغة الميل والمقطع على الصورة: y = mx + b ؛ حيث m ≠ 0 هو ميل المُستقيم وَ b المقطع y لهُ. وبما أنَّ التمثيل البيانيّ لهذه المعادلة يجتازُ اختبار الخطِّ الرأسِيِّ فإنَّها تُعَدُّ اقترانًا ، وَيُسَمّى اقترانًا خطيًّا.   • يمكنُ أيضًا كتابةُ قاعدةِ الاقترانِ الخطيِّ باستعمال رمز الاقتران (f(x على الصورةِ الآتيةِ :                f(x) = mx + b وَتُمَثِّلُ قِيَمُ x عناصر مجال الاقتران f، أمّا قِيَمُ (f(x فَتُمَثِّل عناصر مَداهُ.

 

 

 

 

 

 

 

 

مثال : 

إذا كانَ f(x) = 4x + 5 ، فَأُجيبُ عَنِ الأسئلةِ الآتيةِ تِباعًا :

1) أجد  f(2) .

الحل : 

الاقترانُ المُعطى	f(x) = 4x + 5
بتعويض x = 2	f(2) = 4(2) + 5
بالتبسيطِ	= 13

 

 

 

2) أجد  f(-5) + 9

الحل : 

المقدار المُعطى	f(-5) + 9
بتعويض x = -5 في الاقتران f(x)	4(-5) + 5 + 9
بالتبسيطِ	-20 + 14  = - 6

 

 

 

 

1) أجد قيمةَ x التي تجعلُ  7 - = f(x) .

الاقترانُ المُعطى	f(x) = 4x + 5
بتعويض 7 -  = f(x)	- 7 = 4x + 5
بطرح 5 من طرفي المعادلة	-12 = 4x
بقسمة طرفي المعادلة على 4	-3 =  x

 

 

 

 

إذنْ، عندما x = -3 ، فإنَّ f(x) = -7 .

---

•• للاقترانات الخطية تطبيقات حياتية كثيرة.

مثال :

 يُمَثِّلُ الاقترانُ P(x) = 3x ربح معمل من بيع x من الحقائب التي ينتجها أسبوعيًا ، إذا كان الحد الأقصى لإنتاج هذه الحقائب في الأسبوع 50

حقيبة ، أَجِدُ مجالَ الاقترانِ وَمَداهُ.  

الحل : 

المجال : 

أصغر قيمة  لـ  x  تساوي صفر وأكبر قيمة  =  50  ، إذن المجال : $[ 0 , 50]$

المدى : 

أصغر قيمة لـ d(x) عندما x = 0 فإنّ :   0 = (0)d(x) = 3  ، وأكبر قيمة لـ d(x) عندما x = 50  ، إذن : $d\left(50\right) = 3\left(50\right) = 150$

إذن المدى :  $[ 0 , 150]$    

 

---

 

•• أتعلَّمُ : يمكنُ إيجادُ مَدى الاقترانِ الخطيِّ بتعويضِ أقلِّ قيمةٍ وأعلى قيمةٍ في المجالِ.

 

 

---

 

ثالثًا : الاقتراناتُ غيرُ الخطيَّةِ

الاقترانُ غيرُ الخطيِّ :  اقترانٌ لا يمكنُ كتابتُهُ على الصورةِ  f(x) = mx + b ، وتمثيلُهُ البيانيُّ ليسَ خطًّا مستقيمًا.

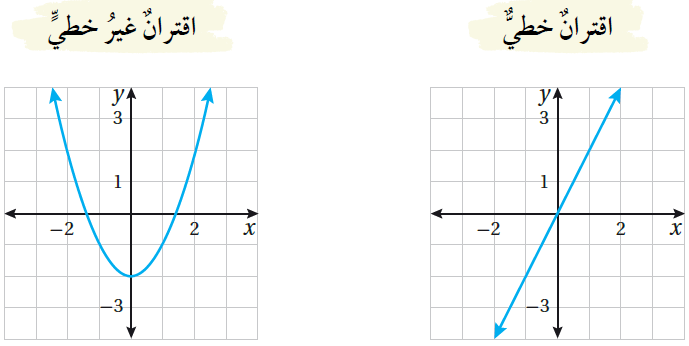
•• أتعلَّمُ : إذا احتوى الاقترانُ (f(x على أيِّ أسٍ غيرِ الواحدِ للمقدارِ x، فإنَّ الاقترانَ غيرُ خطيٍّ.

 

 

يمكنُ إيجادُ قيمةِ الاقترانِ غيرِ الخطيِّ عندَ قيمةٍ مُعَيَّنَةٍ مِنْ خلالِ التعويضِ، ثمَّ اتِّباعِ أولوياتِ العملياتِ.

مراجعةُ المفهومِ (أولوياتُ العملياتِ الحسابيَّةِ)  أولوياتُ العملياتِ الحسابيَّةِ ، هِيَ :  1) أَجِدُ قيمةَ المِقدارِ داخلَ الأقواسِ. 2) أَجِدُ قِيَمَ المقاديرِ الأُسِّيَّةِ والجُذورِ جميعَها. 3) أضرِبُ أوْ أقسِمُ مِنَ اليسارِ إلى اليمينِ(أيُّهُما أسبَقُ). 4) أجمعُ أوْ أطرحُ مِنَ اليسارِ إلى اليمينِ(أيُّهُما أسبَقُ).

 

 

 

 

 

 

 

 

مثال :

إذا كان  $f\left(x\right) = 3x^2 + 4x - 2$  ، فَأَجِدُ كُلًّ ممّا يأتي : 

 $\mathbf{1}\mathbf{)} f \left(2\right)$                                        $\mathbf{2}\mathbf{)} 3f(-3) - f\left(0\right)$     

الحل : 

$\mathbf{1}\mathbf{)} f \left(2\right)$

الاقترانُ المُعطى	$f\left(x\right) = 3x^2 + 4x - 2$
بتعويض x = 2	$f\left(2\right) = 3{\left(2\right)}^2 + 4\left(2\right) - 2$
بالتبسيط	$f\left(2\right) = 18$

 

 

 

---

$\mathbf{2}\mathbf{)} 3f(-3) - f\left(0\right)$

المقدار المُعطى	$3f(-3) - f\left(0\right)$
بتعويض  x = -3  ،  x = 0	$3\mathbf{ }\mathbf{(}3{(-3)}^2 + 4(-3) - 2\mathbf{)}-\mathbf{(}3{\left(0\right)}^2 + 4(0) -2\mathbf{)}$
بالتبسيط	$3\mathbf{ }\mathbf{(}3\times 9-12- 2\mathbf{)}-\mathbf{(}-2\mathbf{)}$
بالتبسيط	$39+2 =\mathbf{ }\mathbf{41}$