تطابقُ المثلثاتِ (ASA, AAS)
أتحققُ من فهمي 1 : في الشكلِ المجاورِ، إذا علمْتُ أنَّ فأثبت أن باستعمالِ البرهانِ ذي العمودَينِ.
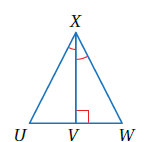
| العبارات | المبررات |
| ضلع مشترك | |
| معطى | |
| زاوية قائمة | |
| ASA |
أتحققُ من فهمي 2 : في الشكلِ المجاورِ، إذا علمْتُ أنَّ وأنًَ زاويتان قائمتان ، فأثبت أنَّ باستعمالِ البرهانِ السهمي .
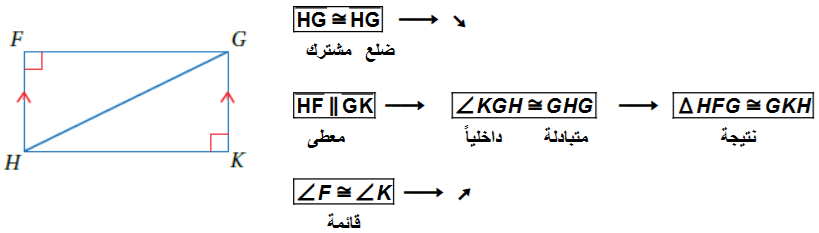
أتحققُ من فهمي 3 : في الشكلِ المجاورِ، إذا علمْت أنَّ : فأثبت أنَّ , باستعمالِ البرهانِ ذي العمودَينِ.
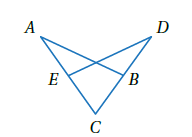
| العبارات | المبررات |
| معطى | |
| معطى | |
| زاوية مشتركة | |
| AAS | |
| ضلعان متناظران في مثلثين متطابقين |
أتحققُ من فهمي 4 :
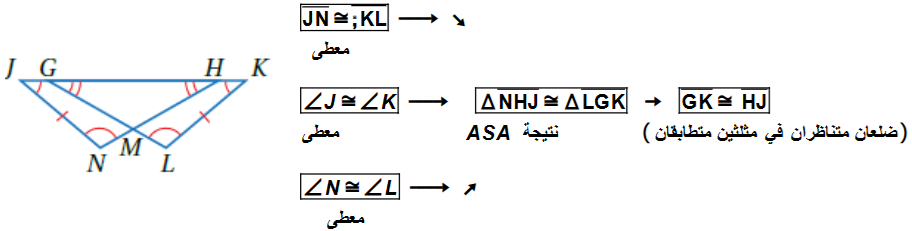
طائرةٌ ورقيةٌ: إذا كانَتْ N في الطائرةِ الورقيةِ المجاورةِ نقطةَ منتصفِ , و فأثبت أنَّ .
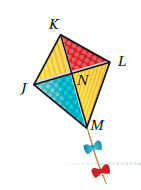
| العبارات | المبررات |
| معطى | |
| لأن N نقطة المنتصف | |
| زاوية قائمة ( ) | |
| ASA | |
| ضلعان متناظران في مثلثين متطابقين |
أتدرب وأحل المسائل :
أحددُ أنَّهُ يمكنُ إثباتُ تطابقِ كلِّ زوجٍ مِنَ المثلثاتِ الآتيةِ أَمْ لا، مبررًا إجابتي:
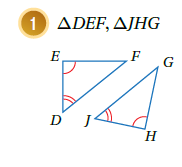
الحل : لا يمكن إثبات التطابق لأن المعطيات لا تكفي ، (زاويتان فقط لا تكفي لإثبات التطابق).
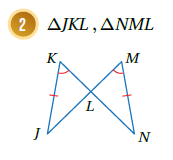
الحل : يمكن إثبات التطابق بزاويتين وضلع غير محصور AAS
حيث :
ملاحظة : ( تقابل بالرأس)
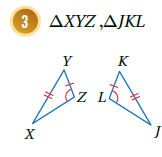
الحل : لا يمكن إثبات التطابق لأن المعطيات لا تكفي ، (ضلعان وزاوية غير محصورة لا تكفي لإثبات التطابق إلا في المثلث قائم الزاوية).
4 ) في الشكلِ المجاورِ، إذا علمْتُ أنَّ ينصف و فأثبت أنَّ .
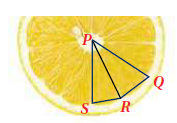
| العبارات | المبررات |
| معطى | |
| نتيجة (لأن تنصف ) | |
| ضلع مشترك | |
| ASA |
A
5) في الشكلِ المجاورِ، إذا علمْتُ أنَّ , , فأثبت أنَّ .
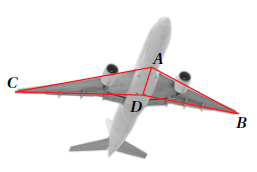
| العبارات | المبررات |
| معطى | |
| معطى | |
| معطى | |
| ASA |
6) أستعمل المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ ذي عمودَينِ؛ لأثبتَ أنَّ
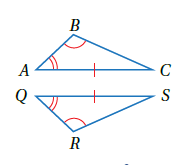
| العبارات | المبررات |
| معطى | |
| معطى | |
| معطى | |
| AAS |
7) استعمل المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ ذي عمودَينِ؛ لأثبتَ أنَّ .
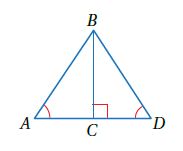
| العبارات | المبررات |
| معطى | |
| معطى | |
| ضلع مشترك | |
| AAS |
8) أستعملُ المعلوماتِ المعطاةَ في الشكلِ الآتي، لكتابةِ برهانٍ سهميٍّ؛ لأثبت أنَّ .
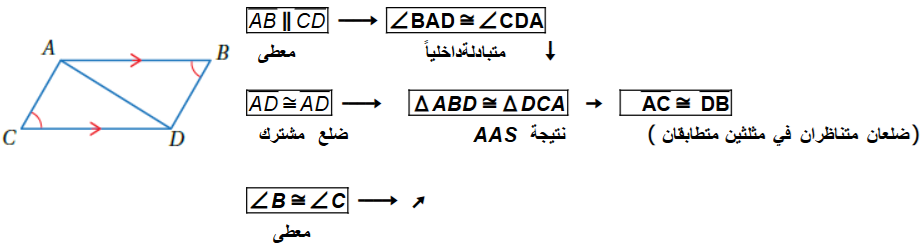
9) أستعملُ المعلوماتِ المعطاةَ في الشكلِ الآتي، لكتابةِ برهانٍ سهميٍّ؛ لأثبتَ أنَّ .
حديقةٌ: تخططُ سالي لزراعةِ حديقتِها مستطيلةِ الشكلِ بأنواعٍ مختلفةٍ مِنَ الزهورِ في أربعةِ أحواضٍ مثلثةِ الشكلِ كما في الشكلِ المجاورِ. إذا علمْتُ أنَّ F نقطة منتصف و فأثبت أنَّ :
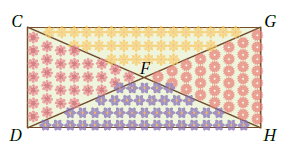
| العبارات | المبررات |
| معطى | |
| معطى | |
| تقابل بالرأس | |
| ASA |
| العبارات | المبررات |
| معطى | |
| معطى | |
| تقابل بالرأس | |
| ASA | |
| ضلعان متناظران في مثلثان متطابقان |
12) نهرٌ: أعودُ إلى فقرةِ (أستكشفُ) بدايةَ الدرسِ، وأثبتُ أنَّ .
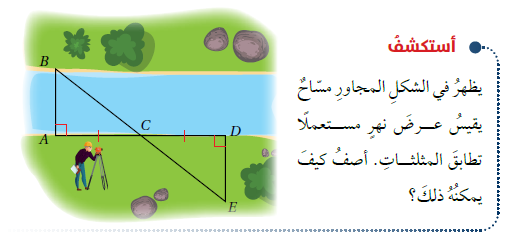
| العبارات | المبررات |
| معطى | |
| معطى (قائمة) | |
| تقابل بالرأس | |
| ASA | |
| ضلعان متناظران في مثلثان متطابقان |
13 ) تحدٍّ: أستعملُ المعلوماتِ المعطاةَ في الشكلِ المجاورِ لكتابةِ برهانٍ ذي عمودَينِ؛ لأثبتَ أنَّ .
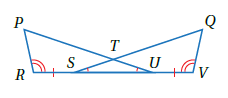
| العبارات | المبررات |
| معطى | |
| معطى | |
| معطى | |
| منطقة مشتركة | |
| ASA |
14) تبريرٌ: هَلْ يمكنُ إثباتُ تطابقِ بالاعتمادِ على المعلوماتِ المعطاةِ على الشكلِ المجاورِ ؟ أبرّرُ إجابتي
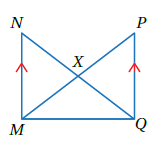 لا ، لا يمكن إثبات التطابق ، لأن المعطيات لا تكفي حيث نحتاج في هذه الحالة إلى ضلعٍ وازويتين متطابقين مع نظائرهم في المثلث الآخر ، ولا نملك منها إلا ضلع مشترك.
لا ، لا يمكن إثبات التطابق ، لأن المعطيات لا تكفي حيث نحتاج في هذه الحالة إلى ضلعٍ وازويتين متطابقين مع نظائرهم في المثلث الآخر ، ولا نملك منها إلا ضلع مشترك.
توضيح : الزاوية المتشكلة من التقابل بالرأس ، والزاوية المتشكلة من التبادل الداخلي بين الضلعين المتوازيين ليس لها فائدة هنا لأنها ليست الزاويا المطلوبة للإثبات .
15) أكتبُُ كيفَ أتحققُ مِنْ تطابقِ مثلثَينِ باستعمالِ زاويتَينِ وضلعٍ محصورٍ بينَهُما؟
يمكن التحقق من خلال مقارنة الزاويا المتناظرة مع بعضها ـ والأضلاع المتناظرة مع بعضها
كتاب التمارين :
أحددُ ما إذا كانَتْ جملةُ التطابقِ صحيحةً أَمْ لا في كلٍّ ممّا يأتي، مبرّرًا إجابتي:
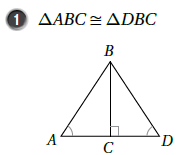 نعم صحيحة ، يمكن إثبات التطابق بزاويتين وضلع غير محصور AAS حيث :
نعم صحيحة ، يمكن إثبات التطابق بزاويتين وضلع غير محصور AAS حيث :
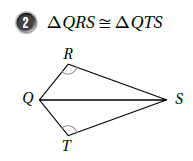
غير صحيحة ، لا يمكن إثبات التطابق ، لأن المعطيات لا تكفي حيث لا نملك إلا ضلع مشترك وزاوية .
غير صحيحة ، المثلثين متطابقين و يمكن إثبات التطابق بزاويتين وضلع غير محصور AAS حيث :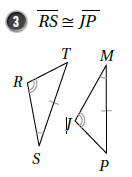
لكن لأن الأضلاع المتطابقة هي :
4) أستعملُ المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ ذي عمودَينِ؛ لأثبتَ أنَّ
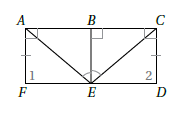
| العبارات | المبررات |
| معطى (قائمة) | |
| معطى | |
| ضلع مشترك | |
| ASA | |
| نتيحة () | |
| نتيحة( ) /تتمة الزاوية القائمة | |
| نتيجة() | |
| معطى | |
| SAS | |
| زاويتان متناظرتان في مثلثان متطابقان |
5) أستعملُ المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ ذي عمودَينِ؛ لأثبتَ أنّ : .
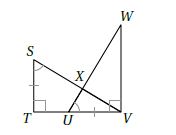
| العبارات | المبررات |
| معطى(زاوية قائمة) | |
| معطى | |
| معطى | |
| ASA |
6) أستعملُ المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ سهميٍّ؛ لأثبتَ أنَّ .
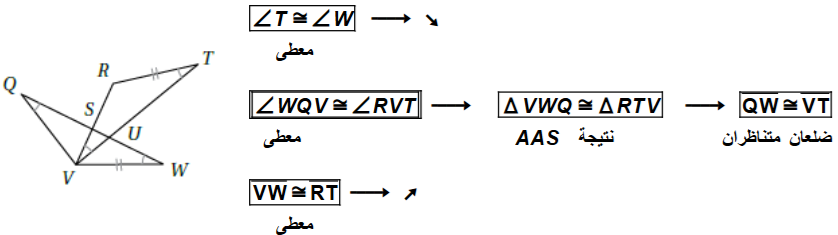
7) في الشكلِ الآتي، إذا علمْتُ أنَّ و ، فأكتبُ برهانًا سهميًّا، لأثبتَ أنَّ .
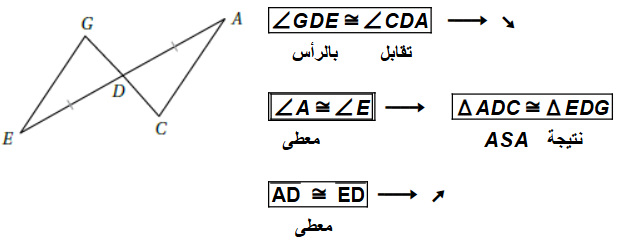
8) أكتشفُ الخطأَ: أكتشفُ الخطأَ في جملةِ التطابقِ الآتيةِ، مبررًا إجابتي:
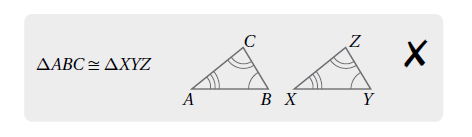
الخطأ هو أنَّ المعطيات هي : ثلاثة زاويا
و لا يمكن إثبات التطابق بثلاثة زوايا ، بل نحتاج على الأقل إلى ضلع واحد .