حلول أسئلة كتاب الطالب وكتاب التمارين
أسئلة أتحقق من فهمي
أتحقق من فهمي صفحة 9
أُحدد إذا كان الزوج المرتب يُمثل حلًا للمتباينة : x + 2y > 1 ، في كلٍّ مما يأتي :
a) (2, 3) b) (1, -2) c) (1, 0)
الحل :
| الزوج المرتب | المتباينة الخطية | التعويض في المتباينة | |
| a) (2 , 3) | x + 2y > 1 |
2 + 2(3) 1 8 > 1 ✔ |
عبارة صحيحة إذن الزوج المرتب (2 , 3) حل لهذه المتباينة |
| b) (1, -2) | x + 2y > 1 |
1 + 2 (-2) 1 -3 1 ✘ |
عبارة غير صحيحة إذن الزوج المرتب (2 - ، 1) ليس حلًا لهذه المتباينة |
| c) (1, 0) | x + 2y > 1 |
1 + 2(0) 1 1 1 ✘ |
عبارة غير صحيحة إذن الزوج المرتب (0 ، 1) ليس حلًا لهذه المتباينة |
أتحقق من فهمي صفحة 11
أُمثِّل المتباينة الخطية : 4x - 5y ≥ 2 على المستوى الإحداثي.
الحل :
الخطوة 1 : تمثيل المستقيم الحدودي 2 = 4x - 5y
| 0.5 | 0 | x |
| 0 | 0.4 - | y |
أُعيِّن النقطتين ( 0.4 - , 0) و (0 ,0.5) على المستوى الإحداثي ، ثم أرسم مستقيمًا يمر بهما. وبما أنَّه توجد مساواة في رمز المتباينة فإنَّ المستقيم الحدودي يُرسَم متصلًا
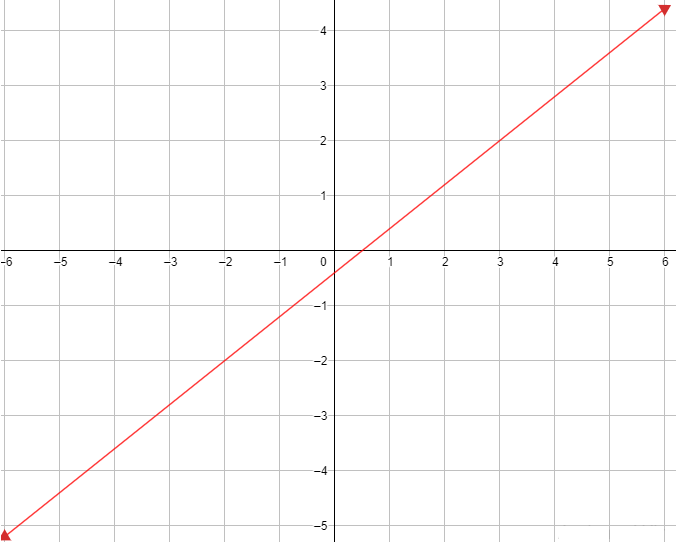
الخطوة 2 : تحديد منطقة الحلول المُمكِنة.
أختار نقطة لا تقع على المستقيم الحدودي ، مثل (2 , 2) ، ثم أتحقَّق إذا كان الناتج صحيحًا أم لا عند تعويضها في المتباينة :
الخطوة 3 : تظليل منطقة الحلول المُمكِنة.
بما أنَّ النقطة ( 2 , 2) لا تحقق المتباينة ، إذن أظلل المنطقة التي لا تقع فيها النقطة ( 2 , 2)
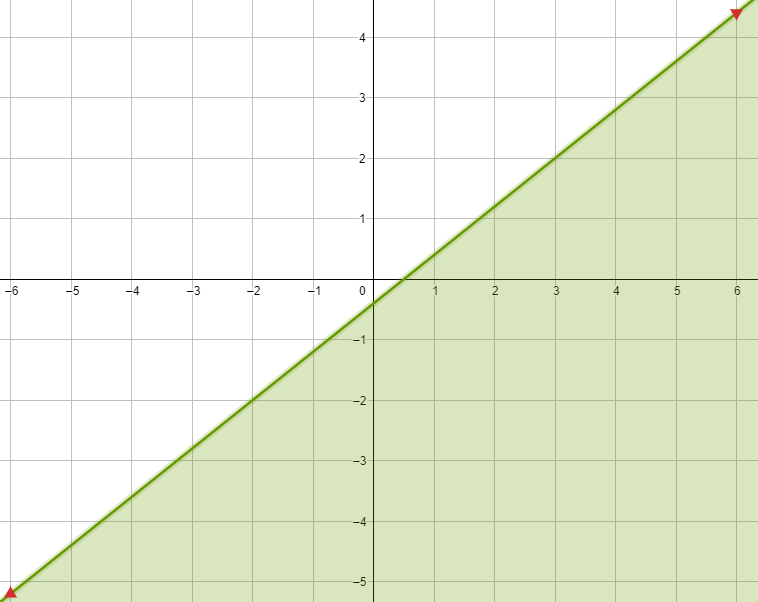
أتحقق من فهمي صفحة 13
مطاعم: مطعم مساحة صالته 64 ، وهي تتَّسع لعدد x من الطاولات الصغيرة، وعدد y من الطاولات الكبيرة. تشغل الطاولة الصغيرة مساحة 2.5 ، وتشغل الطاولة الكبيرة مساحة . أجد عدد الطاولات الصغيرة والكبيرة التي يُمكن وضعها في صالة المطعم.
الحل :
الخطوة 1 : التعبير عن المسألة جبريًّا بمتباينة خطية.
المساحة التي ستشغلها الطاولات الصغيرة = (عدد الطاولات الصغيرة مضروبًا في المساحة التي ستشغلها الطاولة الواحدة)
المساحة التي ستشغلها الطاولات الكبيرة = (عدد الطاولات الكبيرة مضروبًا في المساحة التي ستشغلها الطاولة الواحدة)
إذن المتباينة :
الخطوة 2 : تمثيل المتباينة بيانيًّا.
1) رسم المستقيم الحدودي :
| 25.6 | 0 | x |
| 0 | 16 | y |
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة ، ثم تحديد منطقة الحل .
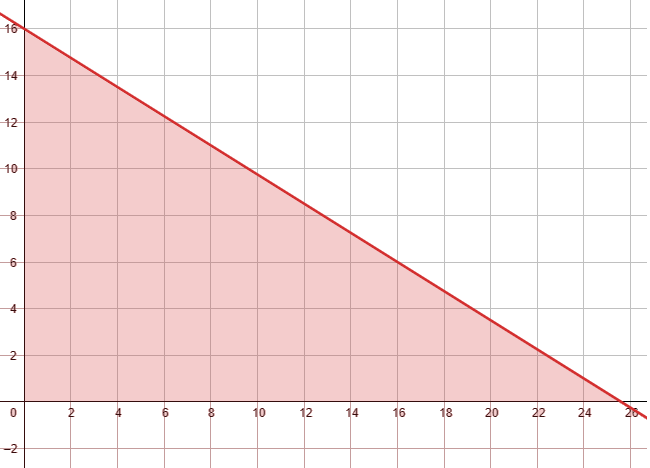
•• هنا تنحصر منطقة الحل في الربع الأول من المستوى الإحداثي ؛ لأن أعداد الطاولات لا يكون سالبًا ، ويُؤخذ من منطقة الحل الأعداد الصحيحة فقط لأن أعداد الطاولات لا يكون إلا عددًا صحيحًا .
أسئلة أتدرب وأحل المسائل
أُحدّد إذا كان كل زوج مُرتب مما يأتي يُمثل حلًا للمتباينة : x - 3y ≥ 5 :
1) (1, -2) 2) (5, 0) 3) (-4, 1)
4) (-3, -4) 5) (- 4, 0) 6) (5, 2)
الحل :
| التعويض في المتباينة | المتباينة الخطية | الزوج المرتب | |
|
عبارة صحيحة إذن الزوج المرتب (2- , 1) حل لهذه المتباينة |
1 - 3(-2) 5 7 5 ✔ |
x - 3y ≥ 5 | 1) (1, -2) |
|
عبارة صحيحة إذن الزوج المرتب (0 , 5) حل لهذه المتباينة |
5 - 3(0) 5 5 5 ✔ |
x - 3y ≥ 5 | 2) (5, 0) |
|
عبارة غير صحيحة إذن الزوج المرتب (1 , 4 -) ليس حلًا لهذه المتباينة |
- 4 - 3(1) 5 - 7 5 ✘ |
x - 3y ≥ 5 | 3) (-4, 1) |
|
عبارة صحيحة إذن الزوج المرتب (4- , 3-) حل لهذه المتباينة |
-3 - 3(- 4) 5 9 5 ✔ |
x - 3y ≥ 5 | 4) (-3, -4) |
|
عبارة غير صحيحة إذن الزوج المرتب (0 , 4 -) ليس حلًا لهذه المتباينة |
- 4 - 3(0) 5 - 4 5 ✘ |
x - 3y ≥ 5 | 5) (- 4, 0) |
|
عبارة غير صحيحة إذن الزوج المرتب (2 , 5) ليس حلًا لهذه المتباينة |
5 - 3(2) 5 - 1 5 ✘ |
x - 3y ≥ 5 | 6) (5, 2) |
أُحدّد إذا كان كل زوج مُرتب مما يأتي يُمثل حلًا للمتباينة : 5x - 2y < 6 :
7) (0, 0) 8) (2, 2) 9) (4, 1)
10) (-2, -1) 11) (-2, -8) 12) (-1, -6)
الحل :
| التعويض في المتباينة | المتباينة الخطية | الزوج المرتب | |
|
عبارة صحيحة إذن الزوج المرتب (0 , 0) حل لهذه المتباينة |
5(0) - 2(0) < 6 ✔ | 5x - 2y < 6 | 7) (0, 0) |
|
عبارة غير صحيحة إذن الزوج المرتب (2 , 2) ليس حلًا لهذه المتباينة |
5(2) - 2(2) 6 6 6 |
5x - 2y < 6 | 8) (2, 2) |
|
عبارة غير صحيحة إذن الزوج المرتب (1 , 4) ليس حلًا لهذه المتباينة |
5(4) - 2(1) 6 18 6 |
5x - 2y < 6 | 9) (4, 1) |
|
عبارة صحيحة إذن الزوج المرتب (1- , 2-) حل لهذه المتباينة |
5(-2) - 2(-1) 6 - 3 < 6 ✔ |
5x - 2y < 6 | 10) (-2, -1) |
|
عبارة غير صحيحة إذن الزوج المرتب (8- , 2-) ليس حلًا لهذه المتباينة |
5(-2) - 2(-8) 6 11 6 |
5x - 2y < 6 | 11) (-2, -8) |
|
عبارة غير صحيحة إذن الزوج المرتب (6- , 1-) ليس حلًا لهذه المتباينة |
5(-1) - 2(-6) 6 7 6 |
5x - 2y < 6 | 12) (-1, -6) |
أُمثِّل كلًا من المتباينات الخطية الآتية على المستوى الإحداثي :
13) 8y + 3x < 2 14) 4x ≤ 8 15) 2x - 9y ≥ -3
16) 5y - 8x ≥ 1 17) -3y < 12 18) 6x + 3y > -5
الحل :
13) 8y + 3x < 2
1) رسم المستقيم الحدودي : 8y + 3x = 2
| 0 | x | |
| 0 | y |
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة 8y + 3x < 2 ، ثم تحديد منطقة الحل .
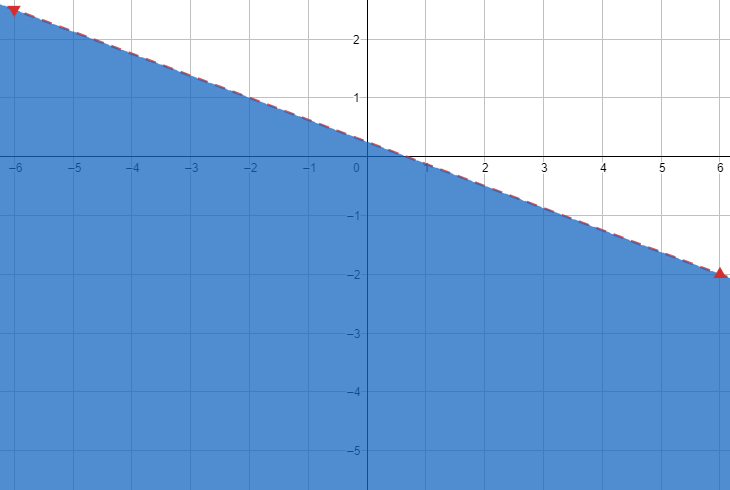
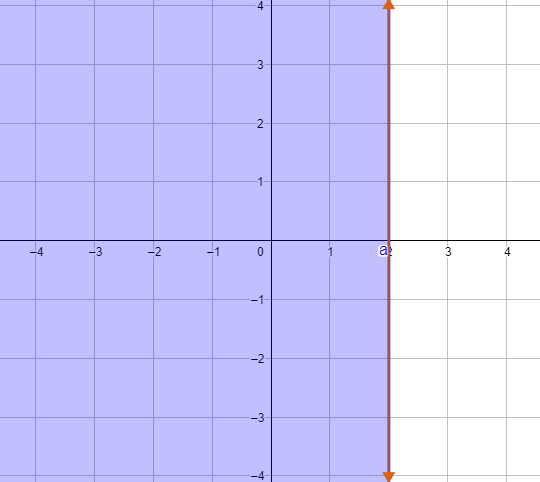
14) 4x ≤ 8
1) رسم المستقيم الحدودي : 4x = 8 ، وهو خط مستقيم يقطع محور x عند x = 2 ويوازي محور y
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة 4x ≤ 8 ، ثم تحديد منطقة الحل .
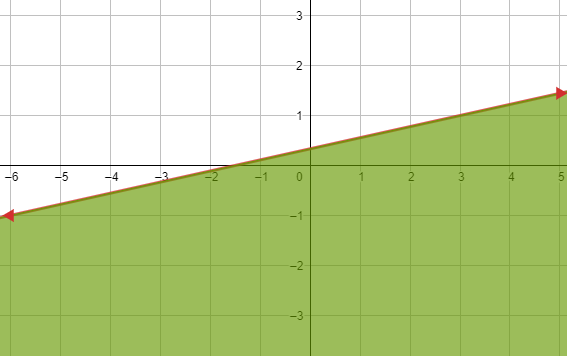
15) 2x - 9y ≥ -3
1) رسم المستقيم الحدودي : 2x - 9y = -3
| 0 | x | |
| 0 | y |
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة 2x - 9y ≥ -3 ، ثم تحديد منطقة الحل .
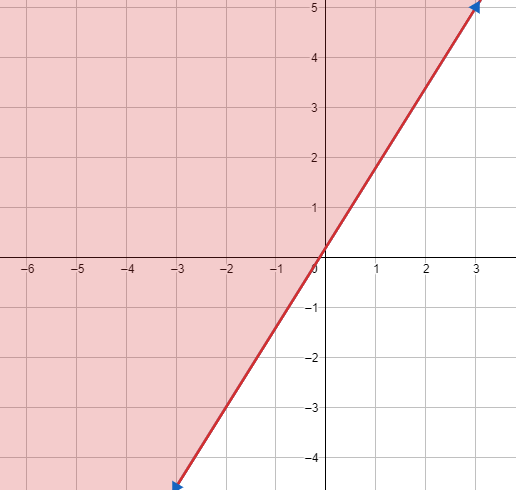
16) 5y - 8x ≥ 1
1) رسم المستقيم الحدودي : 5y - 8x = 1
| 0 | x | |
| 0 | y |
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة 5y - 8x ≥ 1 ، ثم تحديد منطقة الحل .
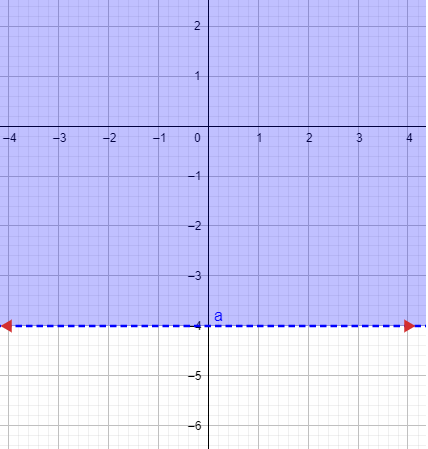
17) -3y < 12
1) رسم المستقيم الحدودي : 3y = 12 - ، وهو خط مستقيم يقطع محور y عند y = - 4 ويوازي محور x
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة 3y < 12- ، ثم تحديد منطقة الحل .
18) 6x + 3y > -5
1) رسم المستقيم الحدودي : 6x + 3y = -5
| 0 | x | |
| 0 | y |
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة 6x + 3y > -5 ، ثم تحديد منطقة الحل .
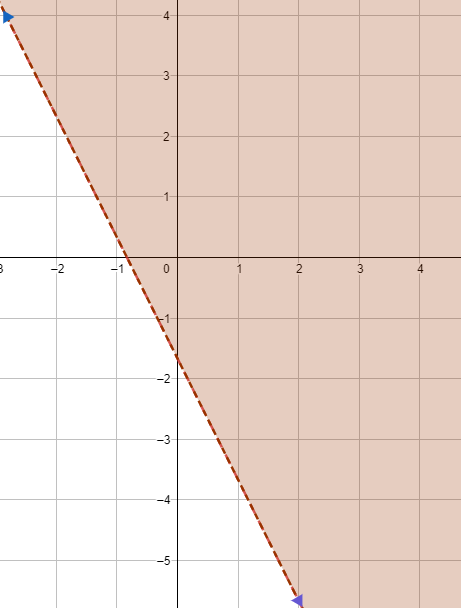
19) اختبارات : تُمثِّل المتباينة : 3x + 2y ≥ 93 عدد أسئلة الاختيار من مُتعدد ( x ) ، وأسئلة ملء الفراغ ( y ) التي يتعيَّن على منى الإجابة عنها بصورة صحيحة لنيل درجة A في اختبار التربية الإسلامية. إذا أجابت إجابة صحيحة عن 20 سؤالًا من أسئلة الاختيار من مُتعدِّد ، وعن 18 سؤالًا من أسئلة ملء الفراغ ، فهل ستنال درجة A في الاختبار؟
الحل :
أعوض x = 20 ، y = 18 في المتباينة 3x + 2y ≥ 93
إذن : ستنال منى درجة A في الاختبار.
20) شاحنات : تستطيع شاحنة حمل من صناديق البضائع. إذا وُجِد عدد x من الصناديق التي كتلة كلٍّ منها ، وعدد y من الصناديق التي كتلة كلٍّ منها ، فما عدد الصناديق التي يُمكِن للشاحنة حملها من كلا النوعين؟
الحل :
المتباينة :
أمثل المتباينة :
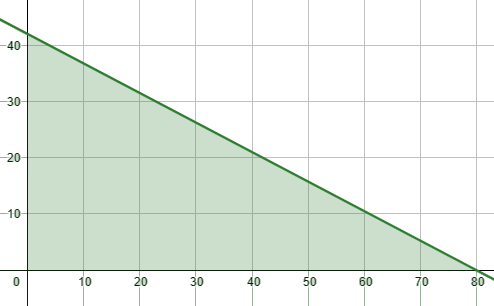
يُؤخذ من منطقة الحل الأعداد الصحيحة الموجبة .
21) أُمثِّل بيانيًّا منطقة حَلِّ المتباينة: x + y < c ، حيث c عدد صحيح موجب.
الحل :
أمثل المتباينة x + y < 1 ، وهي تتضمن قيم c الصحيحة جميعها
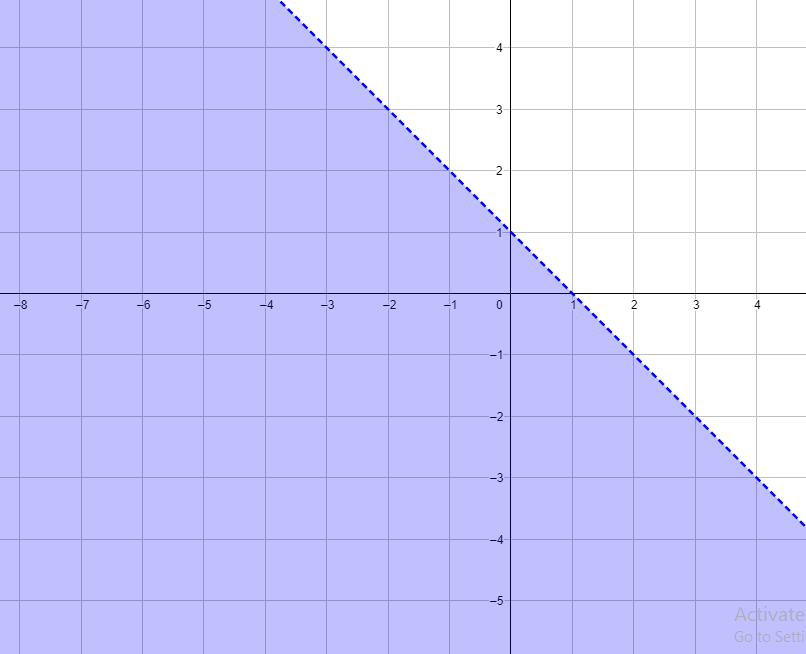
|
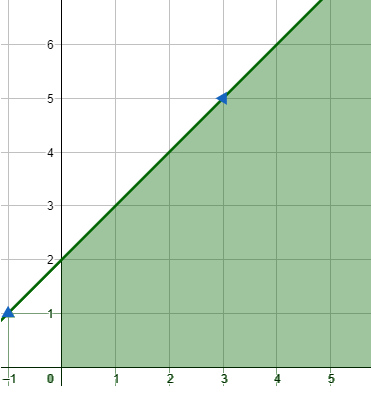
22) أيّ جهتي المستقيم في الشكل المجاور تُمثل منطقة حلّ المتباينة، مُبررًا إجابتي؟ y ≤ x + 2 |
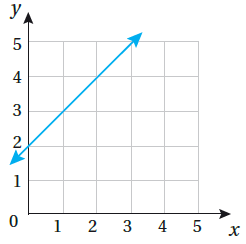 |
الحل : المنطقة التي تمثل حلًا للمتباينة تقع أسفل الخط المستقيم في الربع الأول من المستوى الإحدائي ؛ وذلك لقيود الرسم البياني المُرفق مع المتباينة .
23) أحُلُّ المسألة الواردة في بند (مسألة اليوم).
مسألة اليوم : تصنع نهى أساور وأطواقًا من الخرز ، وتستعمل 10 حبّات من الخرز لصنع السِّوار الواحد، و 45 حبَّة لصنع الطوق الواحد.
كم سِوارًا وطوقًا يُمكِنها أنْ تصنع من 214 حبَّة خرز؟
الحل :
أفرض عدد الأساور = x ، وعدد الأطواق = y
المتباينة :
أمثل المتباينة :
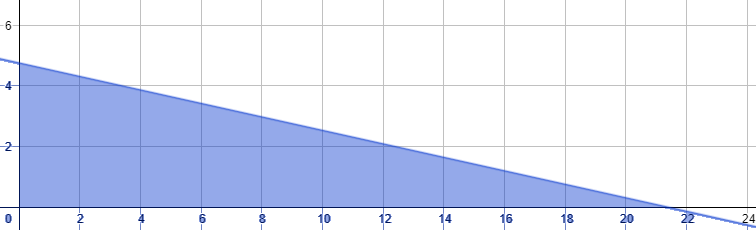
يُؤخذ من منطقة الحل الأعداد الصحيحة الموجبة .
24) أكتشف الخطأ : مثَّل سفيان المتباينة: y ≤ 3x - 2 بيانيًّا على النحو الآتي:
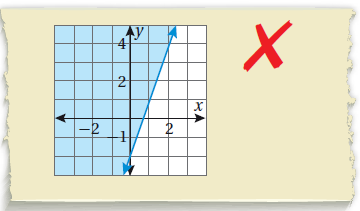
أكتشف الخطأ في تمثيل سفيان، ثم أُصحِّحه.
الحل :
الخطأ الذي وقع فيه سفيان هو تظليل المنطقة الأخرى التي لا تُمثل منطقة الحل .
التمثيل الصحيح :
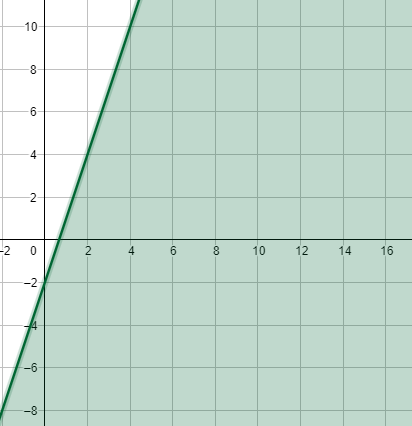
25) تبرير : عند تمثيل متباينة خطية بمتغيرين بيانيًّا، لماذا تُختار فقط نقطة اختبار لا تقع على المستقيم الحدودي؟ أُبرِّر إجابتي.
الإجابة :
لان النقطة التي تقع على المستقيم الحدودي تحقق دائماً المعادلة المرتبطة بالمتباينة.
26) تحدٍّ : أكتب متباينة خطية بمتغيرين، بحيث تقع النقطتان ( 5- , 2-) و ( 5 , 3) على المستقيم الحدودي، وتقع النقطتان ( 5 , 6) و ( 3 , 2) في منطقة الحلول المُمكِنة، ثم أُمثِّل المتباينة بيانيًّا.
الحل :
أجد معادلة الخط المستقيم الحدودي :
أمثل المستقيم في المستوى الإحداثي ، وأعين النقطتين في المستوى لأستنتج من النقطة A أنّ منطقة الحل تقع يمين المستقيم الحدودي ، ومن النقطة B أنّ المستقيم الحدودي من ضمن منطقة الحل ؛ لذا يُرسم متصلًا:
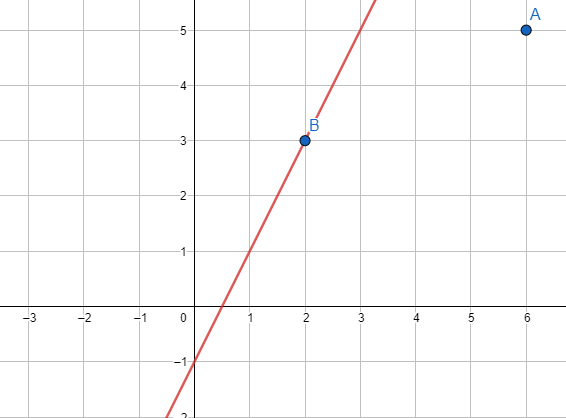
أختبر النقطة A بالتعويض في معادلة المستقيم الحدودي :
إذن المتباينة هي :
أسئلة كتاب التمارين
أُحدد إذا كان الزوج المُرتب يُمثل حلًا للمتباينة : 2x - 8y ≤ - 6 ، في كلٍّ مما يأتي :
1) (1 , 1) 2) (0 , 3) 3) (2 , -3)
الحل :
| التعويض في المتباينة | المتباينة الخطية | الزوج المرتب | |
|
عبارة صحيحة إذن الزوج المرتب (1 , 1) حل لهذه المتباينة |
2(1) - 8(1) - 6 - 6 ≤ -6 ✔ |
2x - 8y ≤ - 6 | 1) (1 , 1) |
|
عبارة صحيحة إذن الزوج المرتب (3 , 0) حل لهذه المتباينة |
2(0) - 8(3) - 6 - 24 ≤ - 6 ✔ |
2x - 8y ≤ - 6 | 2) (0 , 3) |
|
عبارة غير صحيحة إذن الزوج المرتب (3 - , 2) ليس حلًا لهذه المتباينة |
2(2) - 8(-3) - 6 28 - 6 |
2x - 8y ≤ - 6 | 3) (2 , -3) |
4) أُحدِّد المتباينة الخطية التي يُمثِّل الزوج ( 1- , 2) حَلًا لها مما يأتي :
x + y < 1 2x + 3y ≥ 4 5x - y > -2
الحل :
| التعويض في المتباينة | المتباينة الخطية | الزوج المرتب | |
|
عبارة غير صحيحة إذن الزوج المرتب (1 - , 2) ليس حلًا للمتباينة x + y < 1 |
2 + (-1) 1 1 1 |
x + y < 1 | ( 1- , 2) |
|
عبارة غير صحيحة إذن الزوج المرتب ( 1- , 2) ليس حلًا للمتباينة 2x + 3y ≥ 4 |
2(2) + 3(-1) 4 1 4 |
2x + 3y ≥ 4 | ( 1- , 2) |
|
عبارة صحيحة إذن الزوج المرتب ( 1- , 2) حل للمتباينة 5x - y > -2 |
5(2) - (-1) -2 11 > -2 ✔ |
5x - y > -2 | ( 1- , 2) |
أُمثّل كلًا من المتباينات الخطية الآتية على المستوى الإحداثي:
5) 7x - 2y < 5 6) -6x + 4y ≥ -2 7) 5x + 7y ≤ 3
8) -x - y > -1 9) x - 9y ≥ -6 10) -4x - 7y < 8
الحل :
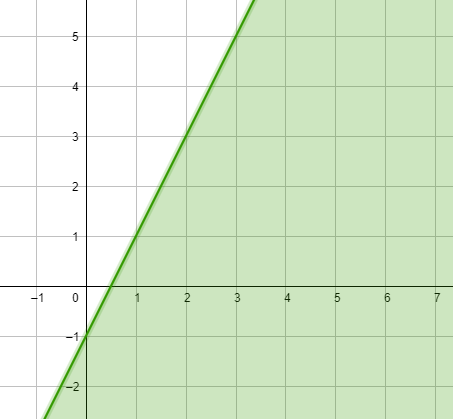
5) 7x - 2y < 5
1) رسم المستقيم الحدودي : 7x - 2y = 5
| 1 | 1 - | x |
| 1 | 6 - | y |
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة 7x - 2y < 5 ، ثم تحديد منطقة الحل .
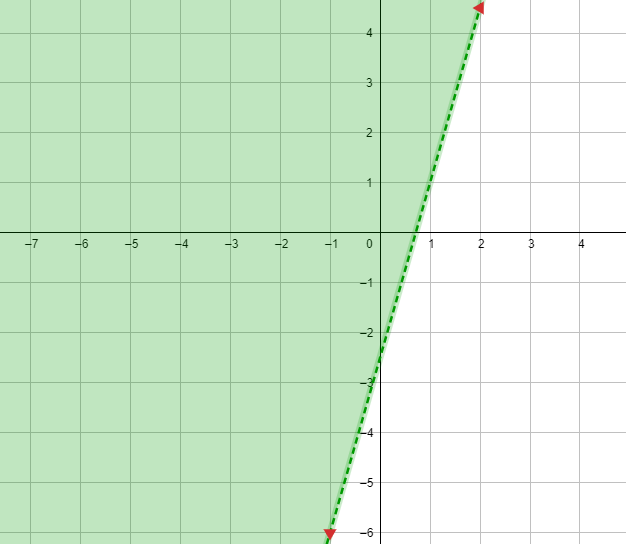
6) -6x + 4y ≥ -2
1) رسم المستقيم الحدودي : 6x + 4y = -2 -
| 1- | 1 | x |
| 2- | 1 | y |
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة 6x + 4y ≥ -2 - ، ثم تحديد منطقة الحل .
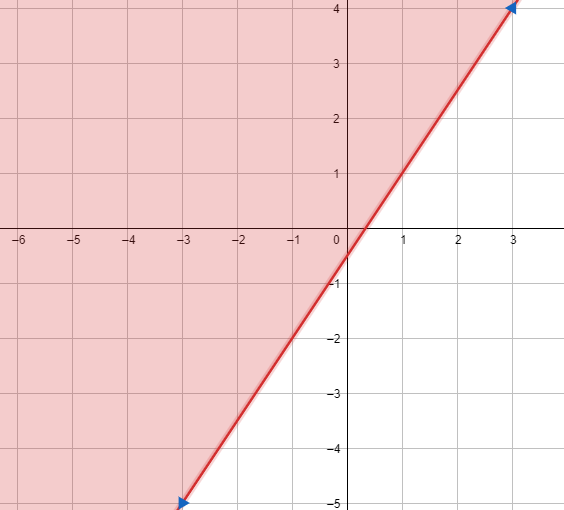
7) 5x + 7y ≤ 3
1) رسم المستقيم الحدودي : 5x + 7y = 3
| 5 - | 2 | x |
| 4 | 1 - | y |
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة 5x + 7y ≤ 3 ، ثم تحديد منطقة الحل .
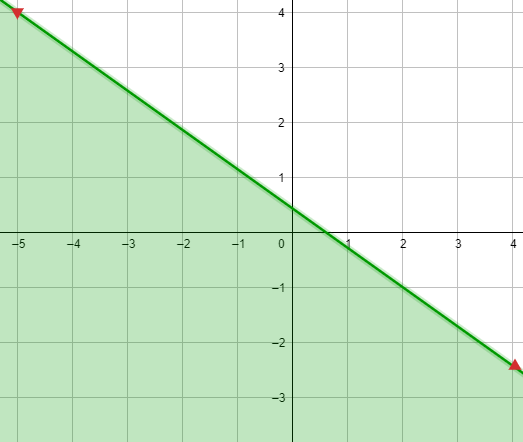
8) -x - y > -1
1) رسم المستقيم الحدودي : x - y = -1 -
| 1 | 0 | x |
| 0 | 1 | y |
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة x - y > - 1 - ، ثم تحديد منطقة الحل .
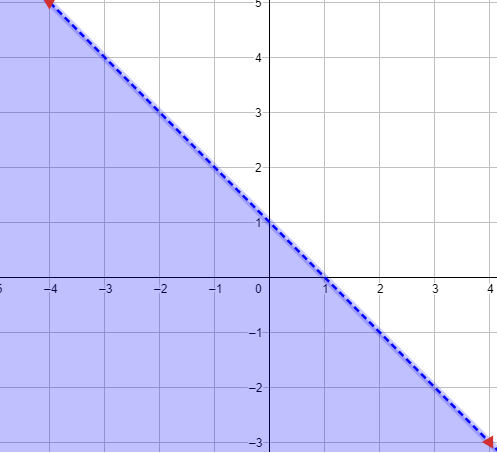
9) x - 9y ≥ - 6
1) رسم المستقيم الحدودي : x - 9y = - 6
| 6 - | 3 | x |
| 0 | 1 | y |
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة x - 9y ≥ - 6 ، ثم تحديد منطقة الحل .
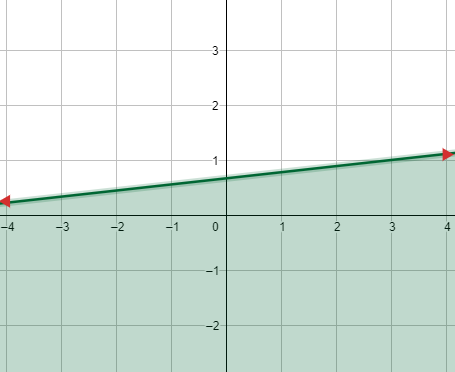
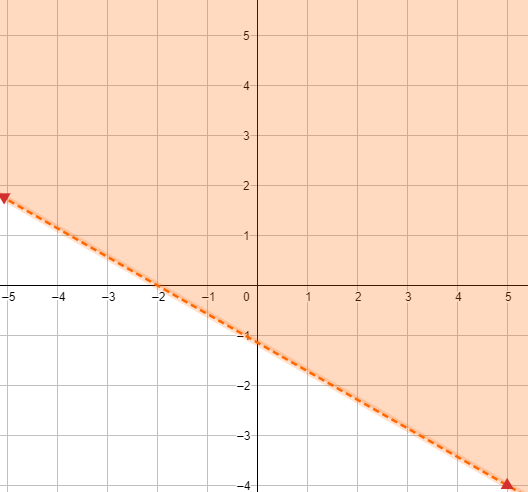
10) -4x - 7y < 8
1) رسم المستقيم الحدودي : 4x - 7y = 8 -
| 2- | 1.5 | x |
| 0 | 2 - | y |
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة 4x - 7y < 8 - ، ثم تحديد منطقة الحل .
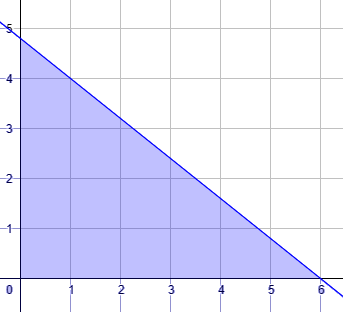
11) طلاء : أراد زياد شراء نوعين من ألوان الطلاء ، سعر النوع الأول دينار واحد لكل كيلوغرام، وسعر النوع الثاني 1.25 دينار لكل كيلوغرام. كم كيلوغرامًا من كل نوع سيشتري زياد إذا كان معه 6 دنانير؟
الحل :
12) مطاعم : يبيع مطعم للوجبات السريعة نوعين من الوجبات، سعر النوع الأول 4 دنانير ، وسعر النوع الثاني 3 دنانير. أجد عدد الوجبات التي يجب بيعها من كل نوع يوميًّا، بحيث لا يقل سعرها عن مصروفات المطعم اليومية التي تبلغ 750 دينارًا.
الحل :
أفرض عدد الوجبات المُباعة من النوع الأول = x ، وعدد الوجبات المُباعة من النوع الثاني = y
المتباينة :
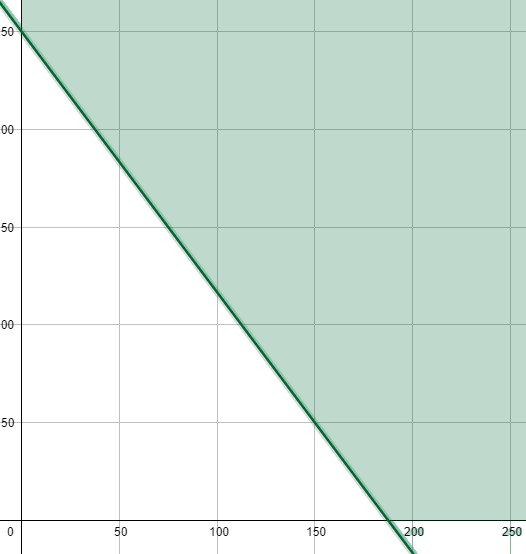
يؤخذ من منطقة الحل الأعداد الصحيحة الموجبة .
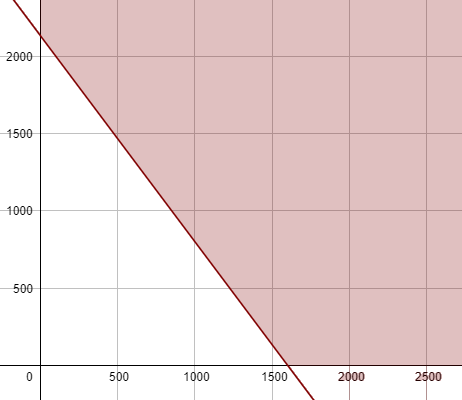
13) صناعة : يُنتِج مصنع نوعين من أنابيب الماء ، سعر النوع الأول ديناران للمتر ، وسعر النوع الثاني 1.5 دينار للمتر. أجد عدد الأمتار التي يُمكِن إنتاجها من كل نوع، بحيث لا تقل إيرادات المصنع عن 3200 دينار يوميًّا.
الحل :
أفرض عدد الأمتار المُباعة من النوع الأول = x ، وعدد الأمتار المُباعة من النوع الثاني = y
المتباينة :
14) تُستعمَل من مادة البلاستيك لصنع خزّان مياه صغير ، وتُستعمَل من المادة نفسها لصنع خزّان مياه كبير. أجد عدد الخزّانات الصغيرة والكبيرة التي يُمكِن صنعها باستعمال من مادة البلاستيك.
الحل :
أفرض عدد الخزانات الصغيرة = x ، وعدد الخزانات الكبيرة = y
المتباينة :
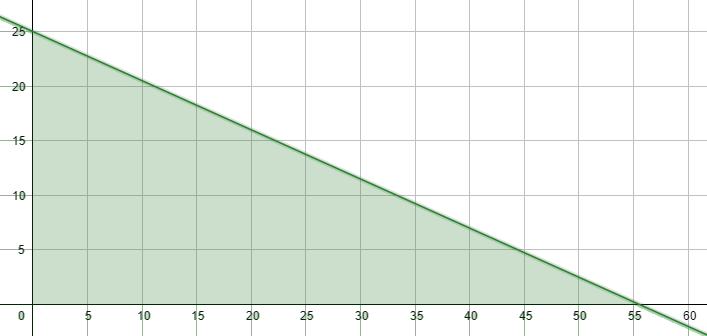
يؤخذ من منطقة الحل الأعداد الصحيحة الموجبة.