حَلُّ المتباينة الخطية بمتغيرين بيانيًا
المتباينة الخطية : جملة رياضية تحوي الرمز ≤ ، أو ≥ ، أو > ، أو < ، وأنَّها قد تحتوي على متغير واحد أو متغيرين. من الأمثلة على المتباينات الخطية بمتغيرين:
•• يكون الزوج المُرتَّب (a , b) حلًا للمتباينة الخطية بمتغيرين إذا كان الناتج صحيحًا عند تعويض إحداثييه في المتباينة.
تمثيل المتباينة الخطية بمتغيرين بيانيًا ، وتحديد منطقة الحلول الممكنة لها
عند تمثيل المتباينة الخطية بيانيًّا على المستوى الإحداثي ، فإنَّ النقاط التي تُمثِّل جميع حلولها المُمكِنة تُسمّى منطقة الحلول المُمكِنة .
•• لتمثيل المتباينة بيانيًّا، أبدأ برسم مستقيم المعادلة المرافقة للمتباينة، التي أحصل عليها باستبدال الرمز ( ≥ ، ≤ ، >، <) برمز المساواة (=) ، حيث تُمثِّل المعادلة الناتجة مستقيمًا يُسمّى المستقيم الحدودي ؛ وهو مستقيم يُقسِّم المستوى الإحداثي إلى جزأين، أحدهما منطقة الحلول المُمكِنة.
قد يكون المستقيم الحدودي جزءًا من منطقة الحلول المُمكِنة إذا تضمَّنت المتباينة الرمز ≤ أو الرمز ≥ ، عندئذٍ يُرسَم المستقيم الحدودي متصلًا كما في الشكل الآتي :
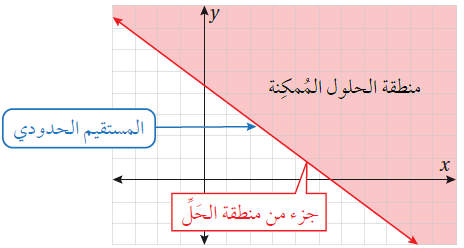
وقد لا يكون المستقيم الحدودي جزءًا من منطقة الحلول المُمكِنة إذا تضمَّنت المتباينة الرمز < أو الرمز >، عندئذٍ يُرسَم المستقيم الحدودي مُتقطِّعًا كما في الشكل الآتي :
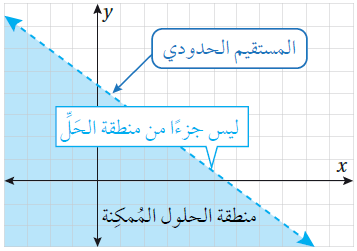
لتحديد أيِّ المنطقتين على جانبي المستقيم الحدودي هي منطقة الحلول المُمكِنة، أختار أيَّ نقطة ( a, b ) لا تقع على المستقيم الحدودي، ثم أُعوِّضها في المتباينة الخطية، فإذا كانت تُحقِّقها (أيْ ينجم عنها نتيجة صحيحة) ، أُظلِّل الجزء من المستوى الإحداثي الذي تقع فيه تلك النقطة، وإلّا أُظلِّل الجزء الآخر الذي لا تقع فيه تلك النقطة.