رياضيات فصل أول

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 109

أَحل كُل من المُعادلات الآتية : 

a) x² - 3x = 0 

المُعادلة المُعطاة	x2 - 3x = 0
بإخراج العامل المُشترك الأكبر	x(x - 3) = 0
خاصيَّة الضَّرب الصِّفريِّ	x = 0  or  x - 3 = 0
بحلِّ كلِّ مُعادلة	x = 0   or   x = 3

  b) 8x² = -12x

 

المُعادلة المُعطاة	8x2 = -12x
بجمع 12x  إلى طَرَفَيِ المُعادلة	8x2 + 12x = 0
بإخراج العامل المُشترك الأكبر	4x(2x + 3) = 0
خاصيَّة الضَّرب الصِّفريِّ	4x = 0  or  2x + 3 = 0
بحلِّ كلِّ مُعادلة	x = 0   or   x = -1.5

---

أتحقق من فهمي صفحة 111

أَحل كُل من المُعادلات الآتية : 

a) x² + 7x = - 6   

 

المُعادلة المُعطاة	x2 + 7x + 6 = 0
بالتحليل إلى العوامل	(x + 6) (x + 1) = 0
خاصيَّة الضَّرب الصِّفريِّ	x + 6 = 0    or   x + 1 = 0
بحلِّ كلِّ مُعادلة	x = - 6   or  x = - 1

---

 b) x² -9x + 8 = 0   

المُعادلة المُعطاة	x2 - 9x + 8 = 0
بالتحليل إلى العوامل	(x - 8) (x - 1) = 0
خاصيَّة الضَّرب الصِّفريِّ	x - 8 = 0    or   x - 1 = 0
بحلِّ كلِّ مُعادلة	x = 8   or  x = 1

---

c) x² - 4x - 21 = 0

المُعادلة المُعطاة	x2 - 4x - 21 = 0
بالتحليل إلى العوامل	(x - 7) (x +3) = 0
خاصيَّة الضَّرب الصِّفريِّ	x - 7 = 0    or   x + 3 = 0
بحلِّ كلِّ مُعادلة	x = 7   or  x = -3

---

أتحقق من فهمي صفحة 112

أَحل كُل من المُعادلات الآتية : 

a) 4x² - 1 = 0     

المُعادلة المُعطاة	4x2 - 1 = 0
بتحليل الفرق بين مربعين	(2x - 1) (2x + 1) = 0
خاصيَّة الضَّرب الصِّفريِّ	2x - 1 = 0   or  2x + 1 = 0
بحلِّ كلِّ مُعادلة	x = 0.5    or   x = -0.5

---

 b) 2x² - 18 = 0

 

المُعادلة المُعطاة	2x2 - 18 = 0
بقسمة طرفي المُعادلة على 2	x2 - 9 = 0
بتحليل الفرق بين مربعين	(x - 3) (x + 3) = 0
خاصيَّة الضَّرب الصِّفريِّ	x - 3 = 0   or  x + 3 = 0
بحلِّ كلِّ مُعادلة	x = 3    or   x = -3

---

أتحقق من فهمي صفحة 113

أَحُلُّ المُعادلةَ :  $x^2-6x + 9 = 0$

الحل : 

المُعادلة المُعطاة	x2 - 6x + 9 = 0
بتحليلِ المُرَبَّعِ الكاملِ ثلاثِيِّ الحدودِ	(x - 3) (x - 3) = 0
خاصيَّة الضَّرب الصِّفريِّ	x - 3 = 0
بحلِّ المُعادلة	x = 3

---

أتحقق من فهمي صفحة 114

أَحل كُل من المُعادلات الآتية :

a) 4x² - 100 = 0  

المُعادلة المُعطاة	4x2 - 100 = 0
بجمع 100 إلى طرفي المعادلة	4x2 = 100
بأخذ الجذر التربيعي للطرفين	$2x=\pm \sqrt[]{100}$
بالتبسيط	$2x = \pm 10$
بفصلِ الحَلّين	$2x=10 or 2x=-10$
بحل المعادلتين	$x=5 or x=-5$

 

 b) (x - 1)² = 16

 

المُعادلة المُعطاة	(x - 1)2 = 16
بأخذ الجذر التربيعي للطرفين	$x+1=\pm \sqrt[]{16}$
بالتبسيط	$x + 1 = \pm 4$
بطرح 1 من طرفي المعادلة	$x=\pm 4 -1$
بفصلِ الحَلَّيْنِ	$x= 4-1 or x=-4-1$
بالتبسيط	$x=3 or x=-5$

---

أسئلة أتدرب وأحل المسائل

أَحل كُل من المُعادلات الآتية :

1) 4x² + 9x = 0

$x(4x+9)=0$

$x=0 or 4x+9 =0$

$x=0 or x=-\frac{9}{4}$

---

2)  7x² = 6x 

$7x^2-6x=0$

$x(7x-6)=0$

$x=0 or 7x-6=0$

$x=0 or x=\frac{6}{7}$

---

3) x² + 5x + 4 = 0

$(x+4)(x+1)=0$

$x+4=0 or x+1=0$

$x=-4 or x=-1$

---

4) x² - 2x - 15 = 0

$(x-5)(x+3)=0$

$x-5=0 or x+3=0$

$x=5 or x=-3$

---

5) t² - 8t + 16 = 0

$(t-4)(t-4)=0$

$t-4=0\to t=4$

---

6) x² -18x = -32

$x^2-18x+32=0$

$(x-16)(x-2)=0$

$x-16=0 or x-2=0$

$x=16 or x=2$

---

7) x² + 2x = 24

$x^2+2x-24=0$

$(x-4)(x+6)=0$

$x-4=0 or x+6=0$

$x=4 or x=-6$

---

8) x² = 17x - 72

$x^2-17x+72=0$

$x^2-17x+72=0$

$(x-9)(x-8)=0$

$x-9=0 or x-8=0$

$x=9 or x=8$

---

9) 2m² = 50

 $2m^2-50=0$

$m^2-25=0$

$(m-5)(m+5)=0$

$m=5 or m=-5$

---

10) x² - 9 = 0

$(x-3)(x+3)=0$

$x-3=0 or x+3=0$

$x=3 or x=-3$

---

11) x² - 25 = 0

$(x-5)(x+5)=0$

$x-5=0 or x+5=0$

$x=5 or x=-5$

---

$\mathbf{12}\mathbf{)}\mathbf{ }\frac{\mathbf{1}}{\mathbf{3}}{\mathit{x}}^{\mathbf{2}}\mathbf{-}\mathbf{3}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}$ 
 
 $x^2-9=0$

$(x-3)(x+3)=0$

$x-3=0 or x+3=0$

$x=3 or x=-3$

---

13) s² + 20s + 100 = 0

$(s+10)(s+10)=0$

$s+10=0\to s=-10$

---

$\mathbf{14}\mathbf{)}\mathbf{ }{\mathbf{y}}^{\mathbf{2}}\mathbf{+}\frac{\mathbf{1}}{\mathbf{2}}\mathbf{y}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{-}\frac{\mathbf{1}}{\mathbf{16}}$

$y^2+\frac{1}{2}y +\frac{1}{16}=0$

$(y+\frac{1}{4})(y+\frac{1}{4})=0$

$y+\frac{1}{4}=0\to y=-\frac{1}{4}$

---

15) 9m² - 12m + 4 = 0

$(3m-2)(3m-2)=0$

$3m-2=0\to m=\frac{2}{3}$

---

16) (x + 1)² = 4

$x+1=\pm \sqrt[]{4}$

$x+1=\pm 2$

$x=\pm 2-1$

$x=1 or x=-3$

---

17) 9(x - 1)² = 16

$3(x-1)=\pm \sqrt[]{16}$

$3(x-1)=\pm 4$

$3(x-1)=4 or 3(x-1)=-4$

$x-1=\frac{4}{3} or x-1=-\frac{4}{3}$

$x=\frac{7}{3} or x=-\frac{1}{3}$

---

18) 5x² + 2 = 6

$5x^2-4=0$

$(\sqrt[]{5}x-2) (\sqrt[]{5}x+2)=0$

$\sqrt[]{5}x-2=0 or \sqrt[]{5}x +2=0$

$x=\frac{2}{\sqrt[]{5}} or x=-\frac{2}{\sqrt[]{5}}$

---

19) فُرشاةٌ: سقطتْ فرشاةُ طلاءٍ منْ يدِ سفيانَ. إذا مَثَّلَ الاقترانُ h(t) = 3 - 5t² ارتفاعَ تلكَ الفُرشاةِ بالأمتارِ عَنِ الأرضِ، بعدَ t ثانيةً مِنْ سُقوطِها،

فبعدَ كَمْ ثانيةً تصلُ إلى الأرضِ؟

الحل : 

$3-5t^2=0 \Rightarrow t=\pm \sqrt[]{\frac{3}{5}}$

يُهمل الحل السالب ؛ إذن $t=\sqrt[]{\frac{3}{5}}\approx 0.8$  ، بعد 0.8 من الثانية تصل الفرشاة إلى الأرض .

---

 أعمارٌ: إذا كانَ عمرُ لينةَ x عامًا، ويكبُرُها زوجُها بثلاثةِ أعوامٍ ، وكانَ حاصلُ ضربِ عمريهِما 700 ، فَأَجِدُ:

20) مُعادلةً تربيعيَّةً تُمَثِّلُ الموقفَ.

الحل : 

عمر لينة x  ، غمر زوجها x + 3

المعادلة التربيعية : $x(x+3) = 700$

21) عمرَ لينةَ.

$x(x+3)=700$

$x^2+3x-700=0$

$(x+28)(x-25)=0$

$x+28=0 or x-25=0$

$x=-28 or x=25$

يُهمل الحل السالب ، إذن عمر لينة 25 .

---

22) حديقةٌ : حديقةٌ مستطيلةُ الشكلِ يزيدُ طولُها على عرضِها بمقدارِ 40 m ، ومساحتُها 48000 m² ، يريدُ مزارعٌ إحاطَتَها بسياجٍ. أَجِدُ طولَ السِّياجِ.

الحل : 

أفرض العرض x ، إذن الطول x + 40 

المساحة  = الطول $\times$ العرض 

$x(x+40)=48000$

$x^2+40x-48000=0$

$(x+240)(x-200)=0$

$x+240=0 or x-200=0$

$x=-240 or x=200$

يُهمل الحل السالب ، إذن x = 200 

الطول = x + 40  ، إذن الطول = 240 مترًا.

---

 

23) هندسةٌ : يُبَيِّنُ الشكلُ المُجاورُ مثلثًّا مساحتُهُ 40cm2 . أَجِدُ ارتفاعَهُ h، وطولَ قاعدتِهِ.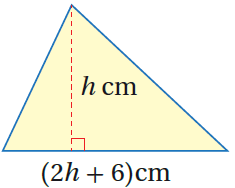

الحل: 

مساحة المثلث = نصف طول القاعدة $\times$ الارتفاع 

$\frac{1}{2}(2h+6)\times h=40$

$h^2+3h=40$

$h^2+3h-40=0$

$(h+8)(h-5)=0$

$h+8=0 or h-5=0$

$h=-8 or h=5$

يُهمل الحل السالب ، إذن h = 5 

الارتفاع 5 مترًا ، طول القاعدة 16 مترًا . 

---

24) أَحُلُّ المسألةَ الواردةَ في بدايةِ الدرسِ.

مسألة اليوم : يُمَثِّلُ الاقترانُ h(t) = -16t ² + 7t ارتفاعَ كنغرٍ بالقدمِ فوقَ سطحِ الأرضِ بعدَ t ثانيةً مِنْ قفزِهِ. كمْ ثانيةً تقريبًا يحتاجُ الكنغرُ ليعودَ إلى

سطحِ الأرضِ؟

الحل : 

$-16t^2+7t=0$ $t(-16t+7)=0$ $t=0 or -16t+7=0$ $t=0 or t=0.4375$

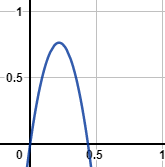يحتاج الكنغر إلى 0.4375 من الثانية ليعود إلى سطح الأرض.  

---

مهاراتُ التفكيرِ العُليا

25) أكتشِفُ الخطأَ: حلَّ سلمانُ ومهنَّدٌ المُعادلةَ التربيعيَّةَ 0 = x² - 3x - 4 ، كما هُوَ مُبَيَّنٌ أدناهُ. أيُّهما إجابتُهُ صحيحةٌ؟  أُبَرِّرُ إجابتي.

 الإجابة : 

 إجابة سلمان صحيحة ؛ لأنه لحل المعادلة (وبحسب خاصية الضرب الصفري) يجب أن يكون الطرف الآخر من المعادلة يساوي صفر.

---

تبريرٌ : أُحَدِّدُ عددَ حلولِ كلِّ مُعادلةٍ ممّا يأتي مِنْ دونِ حَلِّها، مُبَرِّرًا إجابتي:

26) y² = -36          27) a² - 12 = 6                28) n² - 15 = -15
 

الحل : 

26 ) ليس لها حلول حقيقية ؛ لأنه لا يوجد جذر تربيعي لعدد سالب .

27) لها حلان حقيقيان ؛ لأنه بنقل 12 إلى الطرف الآخر فيمكن أخذ الجذر التربيعي للطرفين .

28) يوجد حل واحد ؛ لأنه بنقل 15 إلى الطرف الآخر يصبح صفر ، وبأخذ الجذر التربيعي للطرفين فجذر الصفر يساوي صفر . 

---

29) تبريرٌ : أكتبُ مُعادلةً تربيعيَّةً على الصورةِ القياسيَّةِ، جذراها x = - 4 , x = 6 ، مُبَرِّرًا إجابتي.

الحل : 

x = - 4   أجمع 4 إلى الطرفين تصبح x + 4 = 0 

x = 6    أطرح 6 من الطرفين  تصبح x - 6  = 0 

أضرب المعادلتين الخطيتين :

$$\begin{gathered} (x+4) (x -6) = 0 \\ {x}^2 -2x -24 = 0 \end{gathered}$$

---

أسئلة كتاب التمارين 

أَحل المُعادلات الآتية بالتحليل :

1) 9m² - 18m = 0

$9m^2-18m=0$

$m(m-2)=0$

$m=0 or m-2=0$

$m=0 or m=2$

---

2) x² + 11x + 18 = 0

$(x+9)(x+2)=0$

$x+9=0 or x+2=0$

$x=-9 or x=-2$

---

3) x² - 6x + 8 = 0

$(x-4)(x-2)=0$

$(x-4)(x-2)=0$

$x-4=0 or x-2=0$

$x=4 or x=2$

---

4) x² - 2x - 15 = 0

$(x-5)(x+3)=0$

$x-5=0 or x+3=0$

$x=5 or x=-3$

---

5) x² + 10x = -24

$x^2+10x+24=0$

$(x+6)(x+4)=0$

$x+6=0 or x+4=0$

$x=-6 or x=-4$

---

6) a² -14a + 49 = 0

$(x-7)(x-7)=0$

$x-7=0\to x=7$

---

7) 16t² - 1 = 0

$(4t-1)(4t+1)=0$

$4t-1=0 or 4t+1=0$

$t=\frac{1}{4} or t=-\frac{1}{4}$

---

8) (2x - 1)² = 81

$2x-1=\pm \sqrt[]{81}$

$2x-1=\pm 9$

$2x-1=9 or 2x-1=-9$

$x=5 or x=-4$

---

9) 4(x - 2)² = 25

${(x-2)}^2=\frac{25}{4}x-2=\pm \sqrt[]{\frac{25}{4}}$

$x-2=\pm \frac{5}{2}$

$x-2=\frac{5}{2} or x-2=-\frac{5}{2}$

$x=4.5 or x=-0.5$

---

10) t² + 4t - 12 = 0

$(t+6)(t-2)=0$

$t+6=0 or t-2=0$

$t=-6 or t=2$

---

11) x² + 4x + 4 = 0

$(x+2)(x+2)=0$

$x+2=0\to x=-2$

---

12) 27 -  3y²  =  0

$9-y^2=0$

$(3-y)(3+y)=0$

$3-y=0 or 3+y=0$

$y=3 or y=-3$

---

 

13) هندسةٌ : يُبَيِّنُ الشكلُ المُجاورُ مستطيلً مساحتُهُ $44 c{m}^2$ . أَجِد أبعادَهُ.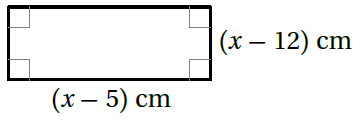

الحل : 

مساحة المستطيل = الطول $\times$ العرض 

$(x-5) (x-12)=44$

$x^2-17x+60=44$

$x^2-17x+16=0$

$(x-1)(x-16)=0$

$x-1=0 or x-16=0$

$x=1 or x=16$

تُهمل x = 1 ؛ لأنها تجعل كل من الطول والعرض سالبيْن ، إذن x = 16  ، وعليه : الطول =  $11 cm$ ، والعرض = $4 cm$

---

14) أَجِدُ عددَيْنِ زَوجِيَّيْنِ مُتَتالِيَيْنِ حاصلُ ضربِهِما 168

الحل : 

أفرض العدد الزوجي الأول x  ، إذن العدد الزوجي التالي هو  x + 2 

$x (x+2)=168$

$x^2+2x=168$

$x^2+2x-168=0$

$(x+14)(x-12)=0$

$x+14=0 or x-12=0$

$x=-14 or x=12$

إذا كانت x = -14  فإن العدد الزوجي التالي هو  x + 2  ، أي 12 -  

وإذا كانت x = 12  فإن العدد الزوجي التالي هو x + 2  ، أي 14

---

 

15)  يُبَيِّنُ الشكلُ المُجاورُ متوازيَ مستطيلاتٍ طولُهُ يُساوي 4 أمثالِ عرضِهِ، وحجمُهُ $320 m^3$ . أَجِدُ طولَهُ وعرضَهُ.

الحل: 

أفرض العرض x ، إذن الطول 4x 

حجم متوازي المستطيلات  = الطول $\times$ العرض $\times$ الارتفاع 

$x\left(4x\right)\left(5\right)=320$

$x\left(4x\right)\left(5\right)=320$

$20x^2=320\to x^2=16$

$x=\pm \sqrt[]{16}=\pm 4$

العرض = $4m$  ،  الطول = $16m$ 

---

16) أكتشِفُ الخطأَ : حلَّ عامرٌ المُعادلةَ التربيعيَّةَ 39 = 33 - 2x² ، كما هُوَ مُبَيَّنٌ أدناهُ. أكتشِفُ الخطأَ في حَلِّهِ وَأُصَحِّحُهُ.

الإجابة: أخطأ عامر عندما أخذ الجذر التربيعي للطرفين بأخذ الجذر الموجب فقط ويفترض $x = \pm 6$