رياضيات فصل أول

العامل المشترك الأكبر 

 

الفكرة الرئيسية : أجد العامل المشترك الأكبر لعددين .

 

* تسمى العوامل التي يشترك فيها عددان أو أكثر بالعوامل المشتركة ويسمى أكبر هذه العوامل بالعامل المشترك الأكبر ويرمز له بالرمز ( ع.م.أ ) .

 

 

* خطوات الحل :

1- أجد عوامل العددين .

2- أحدد العوامل المشتركة للعددين .

3- اختار أكبر عامل مشترك بينهما

 

مثال : أجد العامل المشترك الأكبر للعددين 60 و 36 .

الجواب : 

 

$\leftarrow$عوامل العدد 60 : 1 , 2 , 3 , 4, 5, 6 , 10, 12, 15, 20, 30, 60.

$\leftarrow$عوامل العدد 36 : 1 ,2, 3 ,4, 6, 9, 12, 18 , 36 . 

ألاحظ أن العوامل المشتركة بين العددين هي : 1, 2, 3, 4, 6, 12  وأن العامل المشترك الأكبر لهما هو 12 .

---

ويمكنني أيضا أن أجد العامل المشترك الأكبر لعددين بطريقة أخرى تعتمد على التحليل الى العوامل الأولية التي تعلمتها في الدرس السابق .

 

خطوات الحل :

1- أحلل العددين الى عواملهما الأولية .

2- أحدد العوام الأولية المشتركة .

3- أجد  ع.م.أ  للعددين بضرب العوامل الأولية المشتركة ( نأخذ عاملا واحدا من كل عاملين أوليين متساويين ) . 

 

مثال : أجد العامل المشترك الأكبر للعددين 84 و 96 . 

الجواب :

$96=\mathbf{2}\times \mathbf{2}\times 2\times 2\times 2\times \mathbf{3} 84=\mathbf{2}\times \mathbf{2}\times \mathbf{3}\times 7$

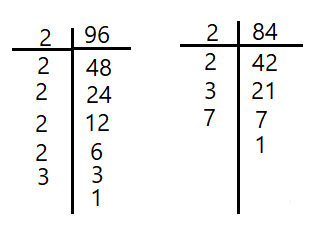
اذن العامل المشترك الأكبر هو 3 × 2 × 2= 12