رياضيات فصل أول

حلول أسئلة درس الاقترانات المتشعبة

أتحقق من فهمي صفحة 10

إذا كان: $f\left(x\right)=\left\{\begin{array}{ll}3x+2& ,x<2\\ 5& ,x=2\\ 2x-1& ,x>2\end{array}\right.$

a) أجد مجال f(x).

b) أجد قيمة كل من f(5) ، و f(2).

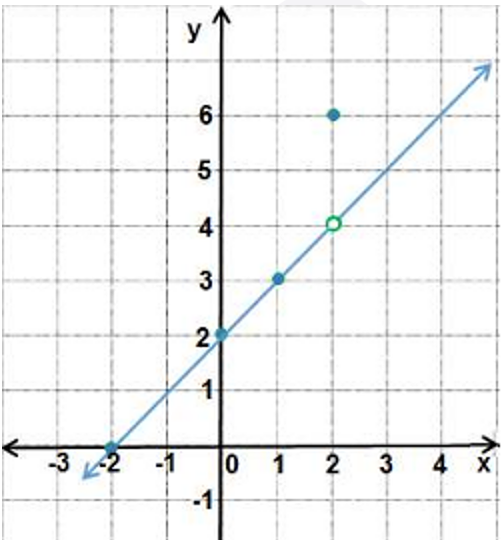
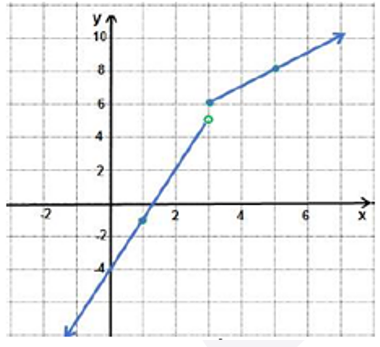
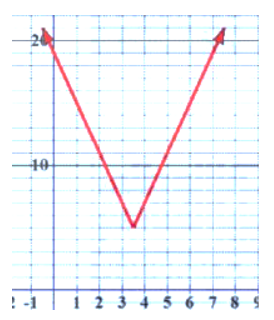
c) أمثل الاقتران f(x) بيانيًا، وأحدد مجاله.

الحل:

a) مجال الاقتران f هو جميع قيم x الحقيقية.

b) $f\left(2\right)=5 , f\left(5\right)=2\left(5\right)-1=9$

c) مدى هذه الاقتران هو مجموعة الاعداد الحقيقية.

---

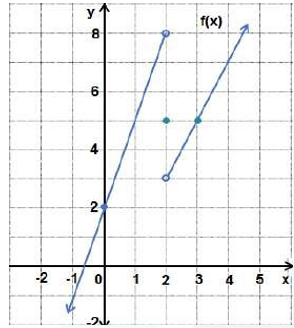
أتحقق من فهمي صفحة 11

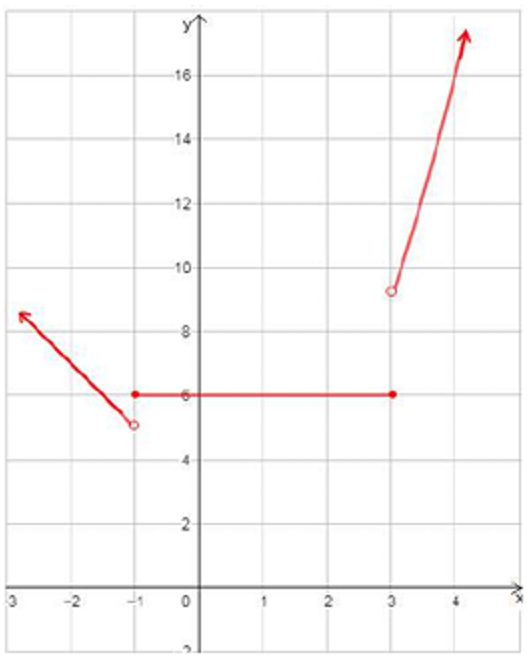
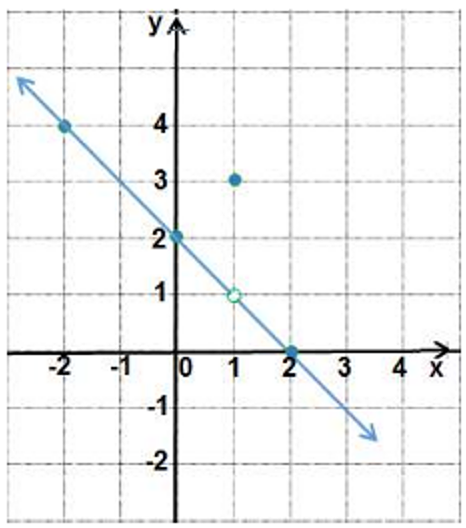
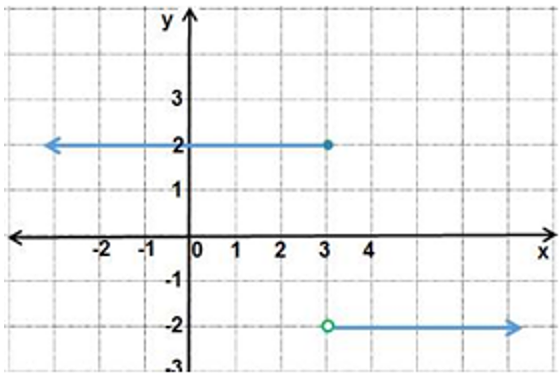
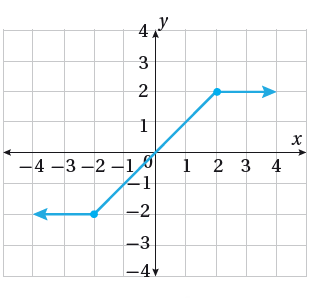
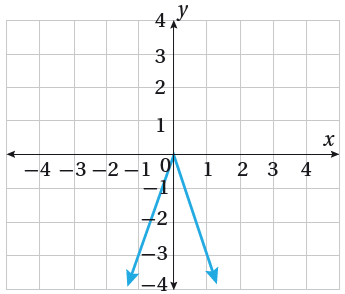
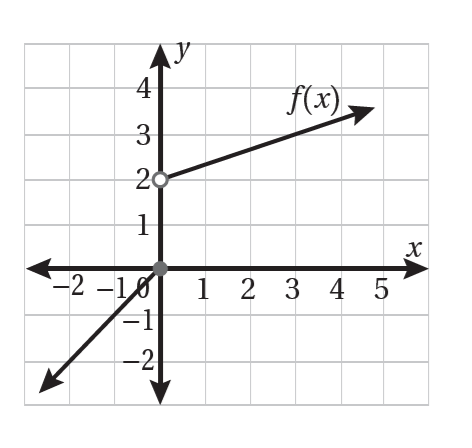
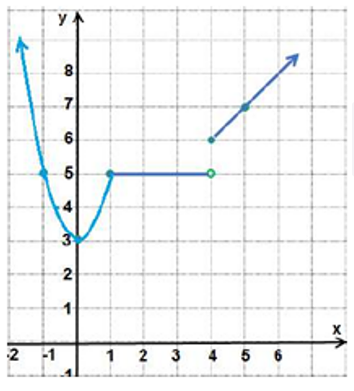
أكتبُ قاعدة الاقتران f(x) الممثل بيانيُا في الشكل المجاور.

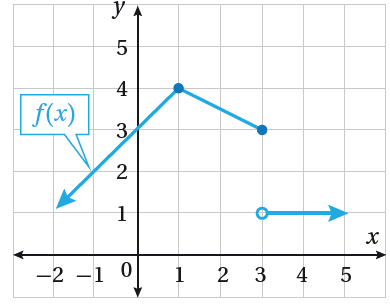
الحل:

$f\left(x\right)=\{\begin{array}{ll}x+3& ,x<1\\ \frac{-1}{2}x+\frac{9}{2}& , 1\le x\le 3\\ 1& , x>3\end{array}$

---

أتحقق من فهمي صفحة 12
زادت شركة رواتب موظفيها الشهرية وفق الأسس الآتية: الرواتب التي تقل عن 400 دينار زيدت بنسبة 15% ، والرواتب من 400 دينار إلى أقل من 600 دينار زيدت بنسبة 10%، مع علاوة ثابتة بقيمة 20 دينارا، والرواتب من 600 دينار وأكثر زيدت 80 دينارا. أكتبُ اقترانا متشعبا لحساب الراتب الجديد لموظفي الشركة.
الحل:

$f\left(x\right)=\{\begin{array}{ll}1.15x & ,x<400\\ 1.1x& , 400\le x\le 600\\ x+80& , x>600\end{array}$

---

أتحقق من فهمي صفحة 13
أُعيد تعريق اقتران القيمة المطلقة: $f\left(x\right)=|3x-9|$

الحل:

$3x-9=0 \to 3x=9 \to x=3$

$f\left(x\right)=\{\begin{array}{ll}-(3x-9) & , x<3\\ 3x-9& , x\le 3\end{array}$

---

أتحقق من فهمي صفحة 15
أُمثل بيانيا كل اقتران مما يأتي، وأحدد مجاله ومداه:

$a) f(x)=|2x|$

$b) f(x)=|2-\frac{1}{2}x|$

الحل:

a) المجال مجموعة الاعداد الحقيقية والمدى $[0,\infty )$ 

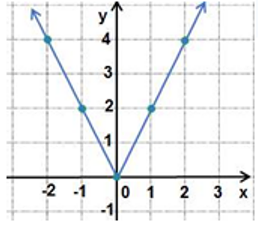
b) المجال مجموعة الاعداد الحقيقية والمدى $[0,\infty )$

---

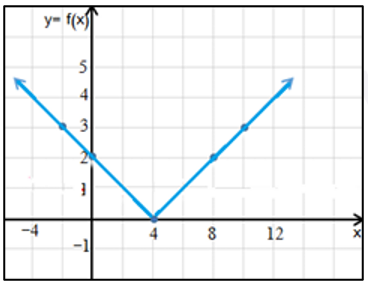
أتحقق من فهمي صفحة 17
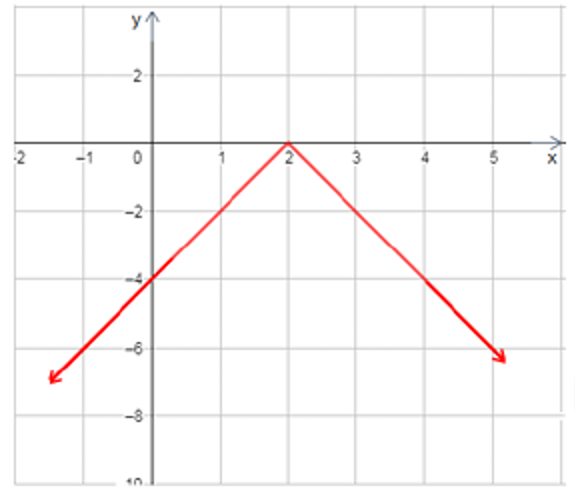
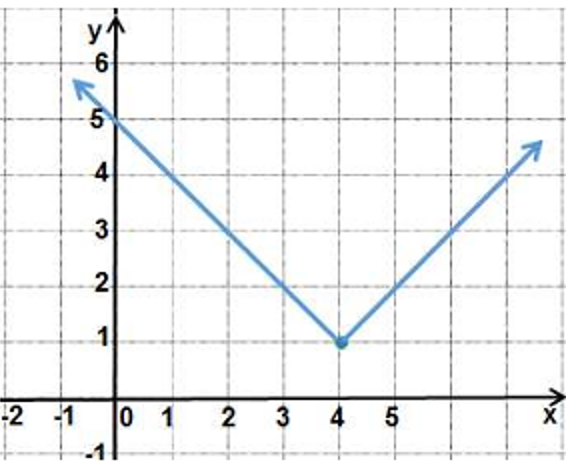
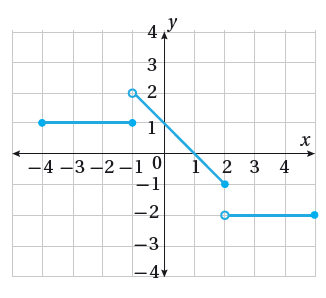
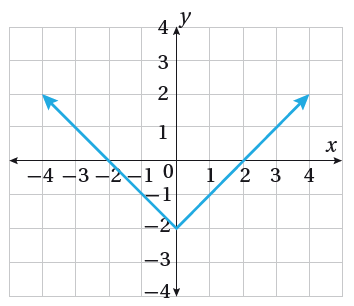
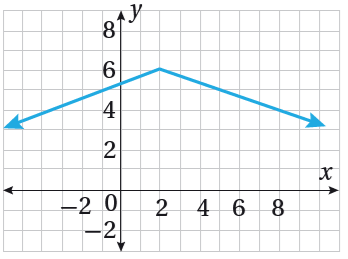
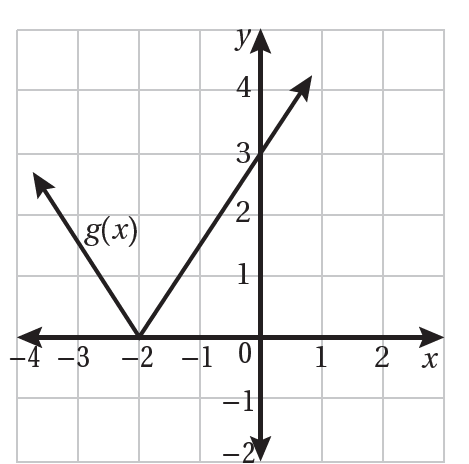
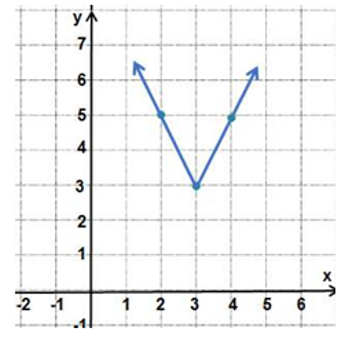
أكتبُ قاعدة اقتران القيمة المطلقة f(x) الممثل بيانيا في الشكل المجاور.

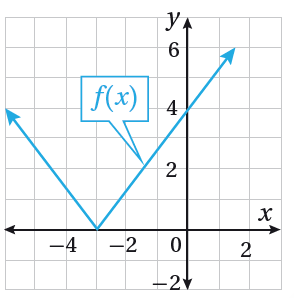
الحل:
$f\left(x\right)=|\frac{4}{3} x+4|$

---

أتدرب وأحل المسائل صفحة 17

إذا كان $f\left(x\right)=\{\begin{array}{ll}3x^2& ,x<-1\\ 4x-3& ,-1\le x\le 4\\ 2& ,x>4\end{array}$    ، فأجد كلا من:

3) f(0)	2) f(-1)	1) f(-2)
6) f(5)	5) f(8)	4) f(4)

الحل:

3) $f\left(0\right)=4\left(0\right)-3=-3$	2) $f(-1)=4(-1)-3=-7$	1) $f(-2)=3(-2{)}^2=12$
6) $f\left(5\right)=2$	5) $f\left(8\right)=2$	4) $f\left(4\right)=4\left(4\right)-3=13$

---

أُعيد تعريف كلّ من الاقترانات الآتية:

7) $f\left(x\right) = |3x - 6|$

8) $f\left(x\right) = |7x - 5| + 3$

الحل:

7) $3x-6=0 \to 3x=6 \to x=2$        $f\left(x\right)=\{\begin{array}{ll}-(3x-6) & , x<2\\ 3x-6& , x\ge 2\end{array}$

8) $7x-5=0 \to 7x=5 \to x=\frac{5}{7}$ $f\left(x\right)=\{\begin{array}{ll}-(7x-5)+3 & , x<\frac{5}{7}\\ (7x-5)+3& , x\ge \frac{5}{7}\end{array}$

---

أُمثّل كلاًّ من الاقترانات الآتية بيانيًّا، وأُحدّد مجالها ومداها:

9) $f\left(x\right)=\{\begin{array}{ll}3-2x& ,x<-1\\ 6& ,-1\le x\le 3\\ x^2& ,x>3\end{array}$	10) $f\left(x\right)=\{\begin{array}{ll}3-2x& ,x=1\\ -x+2& ,x\ne 1\end{array}$
11) $f\left(x\right)=\{\begin{array}{ll}x+2& ,x\ne 1\\ 6& ,x=2\end{array}$	12) $f\left(x\right)=\{\begin{array}{ll}2& ,x\le 3\\ -2& ,x>3\end{array}$
13) $f\left(x\right)=-|2x-4|$	14) $f\left(x\right)=|x-4|+1$

الحل:

9) المجال محموعة الاعداد الحقيقية والمدى: $(5,\infty )$	10) المجال مجموعة الاعداد الحقيقية والمدى مجموعة الاعداد الحقيقية .
11) المجال مجموعة الاعداد الحقيقية والمدى مجموعة الاعداد الحقيقية .	12) المجال محموعة الاعداد الحقيقية والمدى: $\{-2,2\}$
13) المجال محموعة الاعداد الحقيقية والمدى: $(-\infty ,0]$	14) المجال محموعة الاعداد الحقيقية والمدى: $[1,\infty )$

---

أكتبُ قاعدة الاقتران المتشعّب الممثّل بيانيًّا في كلّ من الأشكال الآتية:

15)

16)

17)

الحل:

$\mathbf{15}\mathbf{)} \left\{\begin{array}{l}-2 , x\le -2\\ x ,-2<x<2\\ 2 , x\ge 2\end{array}\right.$

$\mathbf{16}\mathbf{)} \{\begin{array}{l}1 ,-4\le x\le -1\\ -x+1 ,-1<x\le 2\\ -2 , 2<x\le 5\end{array}$

$\mathbf{17}\mathbf{)} \{\begin{array}{l}-x+2 , x\ne 1\\ 3 , x=1\end{array}$

---

أكتبُ قاعدة اقتران القيمة المطلقة الممثّل بيانيًّا في كلّ من الأشكال الآتية:

18)

19)

20)

الحل:

$\mathbf{20}\mathbf{)}\mathbf{ }f(x)=-\frac{1}{3}|x-2|+6$

$\mathbf{19}\mathbf{)}\mathbf{ }f(x)=-|3x|$

$\mathbf{18}\mathbf{)}\mathbf{ }f(x)=|x|-2$

---

خيمة: يُمثّل منحنى الاقتران $f\left(x\right) =-1.4 |x - 2.5|+3.5$ حافتَي الوجه الأمامي لخيمة، ويُمثّل  العمود الذي يتوسّط الوجه الأمامي للخيمة محور التماثل، أمّا المحور $x$ فيُمثّله سطح الأرض. 21) أُمثّل الاقتران بيانيًّا. 22) أجد مجال الاقتران ومداه.

 الحل:

21)

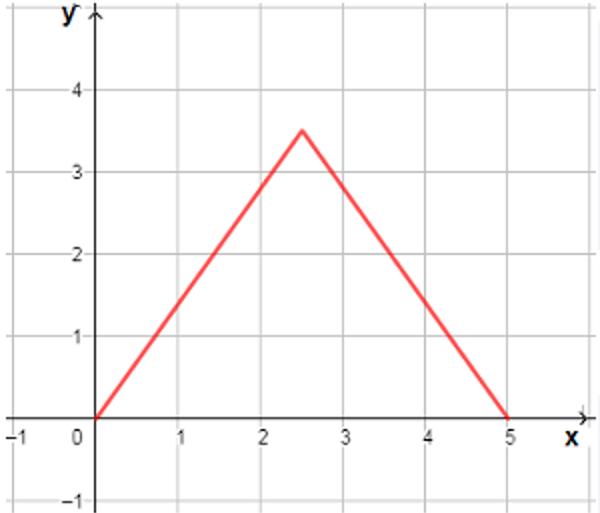
22) مجال هذه الاقتران هو $[0,5]$ ومداه $[0,3.5]$

---

عاصفة: تبدأ العاصفة المطرية بالهطل على شكل رذاذ ثم يزداد معدل الهطل، ثم تعود ثانية للهطل على شكل رذاذ، ويُمثّل الاقتران $r\left(t\right)=-0.5|t-1|+0.5$ معدل الهطل $r$ (بالإنش لكلّ ساعة)، حيث t الزمن بالساعات منذ بداية الهطل. 23) أُمثّل اقتران معدّل الهطل بيانيًّا. 24) أجد كم ساعة استمر الهطل. 25) بعد كم ساعة كان أعلى معدل هطل؟ أُبرّر إجابتي.

الحل:

23)

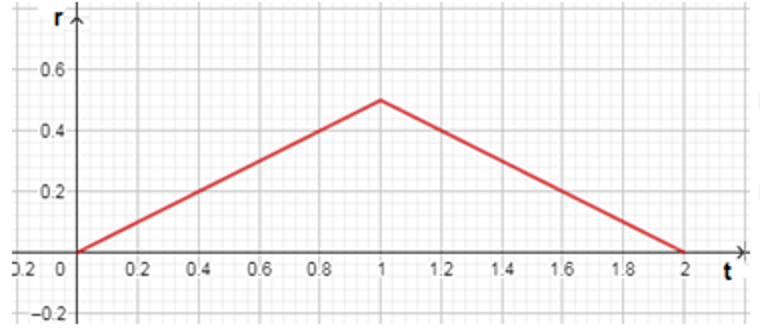
24) استمر الهطل ساعتان لأنه توقف بعد ساعتين، سقطع المنحنى المحور الأفقي عند $0$ و $2$

25) كان أعلى معدل هطل بعد ساعة من بدئه ، يبين الرسم أن القيمة العظمى عند $(1,0.5)$

---

 

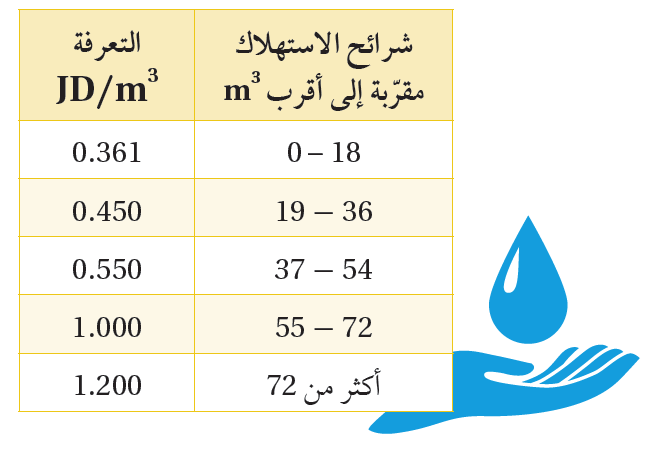
26) أعود إلى مسألة اليوم، وأكتبُ الاقتران المتشعّب الذي يُمكنني استعماله لحساب ثمن المياه لأيّ كمّية مستهلكة.   مسألة اليوم: يُبيّن الجدول المجاور تعرفة ثمن المياه للاستهلاك المنزلي في الدورة الواحدة لبعض شرائح الاستهلاك. كم تدفع أسرة استهلكت 42m3 من الماء؟

الحل:

$f\left(x\right)= \{\begin{array}{l}0.316x ,0\le x\le 18\\ 0.450x-1.602 ,18<x\le 36\\ 0.550x-5.202 ,36<x\le 54\\ x-29.502 ,54<x\le 72\end{array}$

 

---

مهارات التفكير العليا

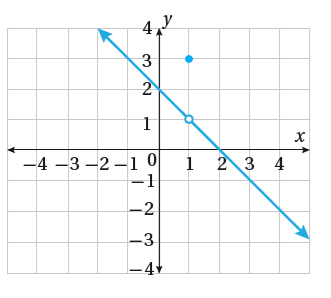
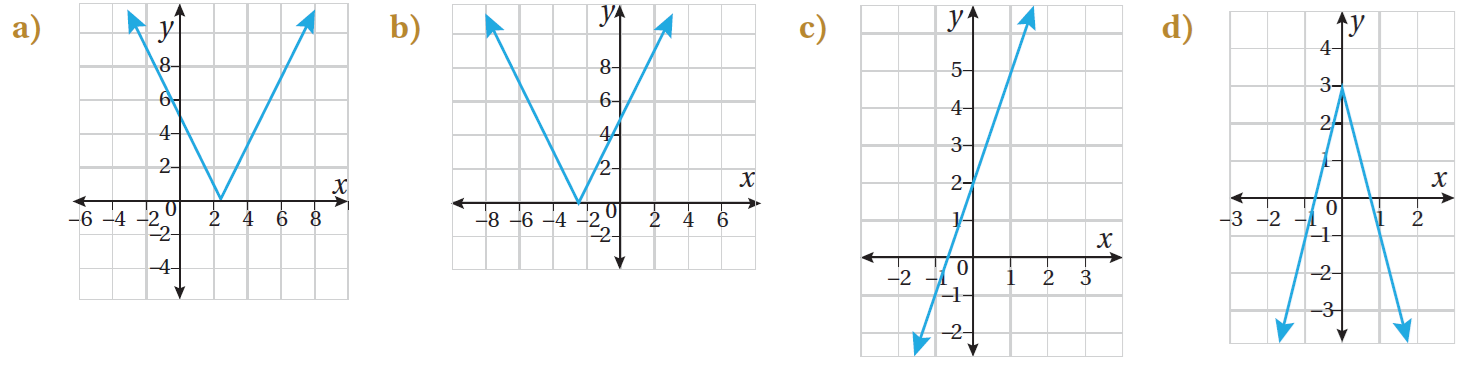
27) تبرير: أيّ الآتية تُمثّل منحنى الاقتران $f\left(x\right) = |2x-5|$ ؟ أُبرّر إجابتي:

الحل:

a ، لأن الرأس عند $(2.5,0)$ ، ومفتوح للأعلى.

---

تحدٍّ: يُمكن كتابة المقدار $x^2+px-q$ على الصورة ${(x-2.5)}^2-0.25$

28) أجد قيمة كل من $P$ و $q$.

29) أجد إحداثيي كل من نقطتي تقاطع منحنى $f\left(x\right)=|x^2+px-q|$ مع محور x.

الحل:

28) $p=-5,q=-6$

29) احداثيا نقطتي تقاطع منحنى f(x) مع المحور x هما $(3,0)$ و $(2,0)$

---

كتاب التمارين

أُعيد تعريف كُلّ من الاقترانات الآتية:

1) $f\left(x\right) = |5x - 4|$

2) $f\left(x\right)=|3-2x|-6$

الحل:

1) $f\left(x\right)=\left\{\begin{array}{l}4-5x ,x<0.8\\ 5x-4 ,x\ge 0.8\end{array}\right.$

2) $f\left(x\right)=\{\begin{array}{l}-2x-3 ,x<1.5\\ 2x-9 ,x\ge 1.5\end{array}$

---

أكتبُ قاعدة الاقتران المعطى تمثيله البياني، في كُلّ ممّا يأتي:

3)

4)

الحل:

3) $f\left(x\right)=1.5|x+2|$

4) $f\left(x\right)=\left\{\begin{array}{l}x ,x<0\\ \frac{1}{3}x+2 ,x\ge 0\end{array}\right.$

---

أُمثّل كُلًًّّا من الاقترانات الآتية بيانيًّا، وأُحدّد مجاله ومداه:

5) $f\left(x\right)=\{\begin{array}{l}3x-4 ,x<3\\ x+3 ,x\ge 3\end{array}$	6) $f\left(x\right)=\{\begin{array}{l}2x^2 + 3 , x<1\\ 5 , 1\le x<4\\ x+2 , x\ge 4\end{array}$
7) $f\left(x\right)=|2x-6|+3$	8) $f\left(x\right)=|4x-14|+5$

الحل:

5) المجال: مجموعة الأعداد الحقيقية  - المدى: $(-\infty ,5)\cup [6,\infty )$	6) المجال: مجموعة الأعداد الحقيقية - المدى $y\ge 3$ أو $[3,\infty )$
7) إحداثيا الرأس: $(\frac{6}{2},3)$ اختار نقطة قبله ، ونقطة بعده لأكون جدول. وأعين النقاط وأرسم شكل V. المجال: مجموعة الأعداد الحقيقية - المدى $y\ge 3$ أو $[3,\infty )$.	8)    المجال: مجموعة الأعداد الحقيقية - المدى $[5,\infty )$

 

---

كهرباء: تزوّد شركة الكهرباء القطاع التجاري بالطاقة الكهربائية مقابل 1.20 دينار شهريًّا (رسومًا ثابتة)، يُضاف إليها 0.121 دينار لكُلّ كيلو واط ساعة لأول 2000 كيلو واط ساعة في الشهر، و 0.176 دينار لكُلّ كيلو واط ساعة من كمّية الاستهلاك الزائدة على 2000 كيلو واط ساعة في الشهر. أكتبُ الاقتران الذي يُعطي قيمة فاتورة الكهرباء بدلالة كمّية الاستهلاك x كيلو واط ساعة شهريًّا.

الحل:

$f\left(x\right)=\left\{\begin{array}{l}1.20+0.121x ,0\le x\le 2000\\ 0.176x-108.80 ,x>2000\end{array}\right.$

---