رياضيات فصل أول

أتحقق من فهمي

ص: 74

أكتب كل معادلة لوغاريتمية مما يأتي، على الصورة الأسية:

$a) {\log }_3 9=2$

$3^2=9$

$b) {\log }_5 5=1$

$5^1=5$

$c) {\log }_4 \left(\frac{1}{256}\right)=-4$

$4^{-4}=\frac{1}{256}$

$d) {\log }_8 1=0$

$8^0=1$

أتحقق من فهمي

ص: 74

أكتب كل معادلة أسية مما يأتي، على الصورة اللوغاريتمية:

$a) {25}^2=625$

$lo{g}_{25} 625=2$

$b) {81}^{\frac{1}{2}}=9$

$lo{g}_{81} 9=\frac{1}{2}$

$c) {\left(10\right)}^{-4}=\frac{1}{10000}$

$lo{g}_{10} \frac{1}{10000}=-4$

$d) {19}^0=1$

$lo{g}_{19} 1=0$

أتحقق من فهمي

ص: 75

أجد قيمة كل مما يأتي، من دون استعمال الآلة الحاسبة:

$a) {\log }_8 64$

$$\begin{gathered} 8^y=64 \\ {8}^y=8^2 \\ y=2 \end{gathered}$$

$b) {\log }_{11} \sqrt{11}$

$$\begin{gathered} {11}^y=\sqrt{11} \\ {11}^y={11}^{\frac{1}{2}} \\ y=\frac{1}{2} \end{gathered}$$

$c) {\log }_{25} 5$

$$\begin{gathered} {25}^y=5^1 \\ {5}^{2y}=5^1 \\ 2y=1 \\ y=\frac{1}{2} \end{gathered}$$

$d) {\log }_2 \frac{1}{8}$

$$\begin{gathered} 2^y=\frac{1}{8} \\ {2}^y=2^{-3} \\ y=-3 \end{gathered}$$

أتحقق من فهمي

ص: 76

أجد قيمة كل مما يأتي، من دون استعمال الآلة الحاسبة:

$a) {\log }_2 64$

$$\begin{gathered} 2^y=64 \\ {2}^y=2^6 \\ y=6 \end{gathered}$$

$b) {\log }_{19} \sqrt{19}$

$$\begin{gathered} {19}^y=\sqrt{19} \\ {19}^y={19}^{\frac{1}{2}} \\ y=\frac{1}{2} \end{gathered}$$

$c) {\log }_{18} 18$

$$\begin{gathered} {18}^y=18 \\ {18}^y={18}^1 \\ y=1 \end{gathered}$$

$d) 4^{{\log }_4 15}$

$15$

أتحقق من فهمي

ص: 78

أستعمل الآلة الحاسبة لإيجاد قيمة كل مما يأتي، مقربا إجابتي إلى أقرب جزء من عشرة:

$a) \log 1200$

$\approx 3.1$

$b) \log (6.3\times {10}^5)$

$\approx 5.8$

$c) \ln 0.00025$

$\approx -8.3$

أتحقق من فهمي

ص:80

أمثل كلا من الاقترانات الآتية بيانيا، وأحدد مجاله ومداه ومقطعيه الإحداثيين وخطوط تقاربه، وإن كان متزايدا أم متناقصا.

$a) f(x)={\log }_3 x$

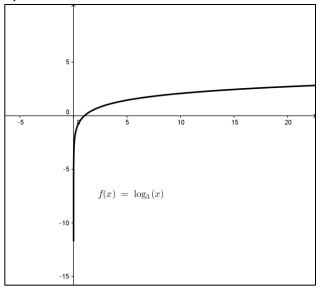
المجال في الفترة $\left(0,\infty \right)$ المدى الأعداد الحقيقية R الاقتران متزايد ليس له مقطع y مقطع x هو x=1 له خط تقارب رأسي هو محور y.

$b) f(x)={\log }_{\frac{1}{3}} x$

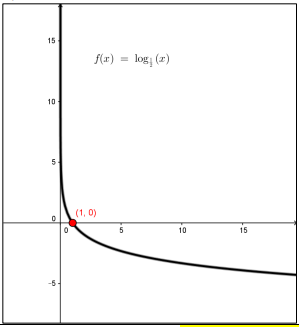
المجال في الفترة $\left(0,\infty \right)$ المدى الأعداد الحقيقية R الاقتران متزايد ليس له مقطع y مقطع x هو x=1 له خط تقارب رأسي هو محور y.

أتحقق من فهمي

ص: 82

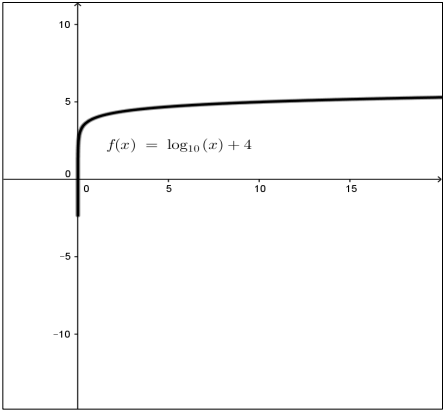
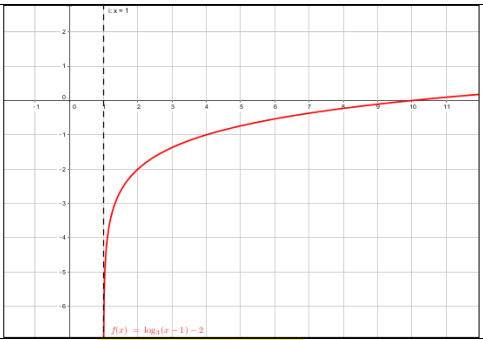
أمثل كل من الاقترانات الآتية بيانيا:

$a) f(x)={\log }_5 (x-2)$

$b) f(x)=\ln (x+3)$

$c) f(x)=\log x+4$

$d) f(x)={\log }_3 (x-1)-2$

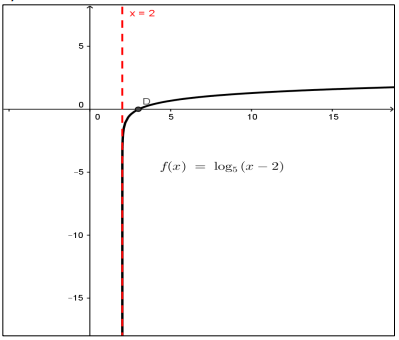
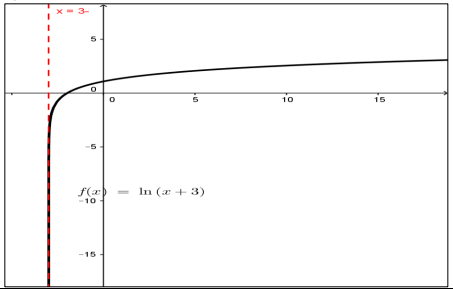
أتحقق من فهمي

ص: 83

أجد الرقم الهيدروجيني (pH) لشامبو طبيعي تركيز أيونات الهيدروجين فيه $5.88\times {10}^{-7} mol/L$، ثم أحدد إذا كان الشامبو حمضيا أم قاعديا. (أقرب إجابتي إلى أقرب جزء من مئة).

$$\begin{gathered} p^H=-log \left[H^{+}\right] \\ {p}^H=-log (5.88\times {10}^{-7})\approx 6.23 \end{gathered}$$

أتدرب وأحل المسائل

أكتب كل معادلة لوغاريتمية مما يأتي، على الصورة الأسية:

$1) {\log }_4 1024=5$

$4^5=1025$

$2) {\log }_3 729=6$

$3^6=729$

$3) {\log }_8 2=\frac{1}{3}$

$8^{\frac{1}{3}}=2$

$4) {\log }_{25} 5=0.5$

${25}^{0.5}=5$

أكتب كل معادلة أسية مما يأتي، على الصورة اللوغاريتمية:

$5) 6^3=216$

$lo{g}_6 216=3$

$6) 3^{-2}=\frac{1}{9}$

$lo{g}_3 \frac{1}{9}=-2$

$7) 5^4=625$

$lo{g}_5 625=4$

$8) 2^{-3}=0.125$

$lo{g}_2 0.125=-3$

أجد قيمة كل مما يأتي، من دون استعمال الآلة الحاسبة:

$9) {\log }_2 256$

$lo{g}_2 2^8=8$

$10) {\log }_9 27$

$$\begin{gathered} 9^y=27 \\ {3}^{2y}=3^3 \\ 2y=3 \\ y=\frac{3}{2} \end{gathered}$$

$11) \log 0.1$

$log {10}^{-1}=-1$

$12) {\log }_{\frac{7}{2}} 1$

$0$

$13) e^{\ln \frac{1}{2}}$

$\frac{1}{2}$

$14) {\log }_y \sqrt[3]{y}$

$lo{g}_y y^{\frac{1}{3}}=\frac{1}{3}$

$15) \log (1.0\times {10}^{-6})$

$log \left({10}^{-6}\right)=-6$

$16) 6^{{\log }_6 2.8}$

$2.8$

أستعمل الآلة الحاسبة لإيجاد قيمة كل مما يأتي، مقربا إجابتي إلى أقرب جزء من عشرة:

$17) \log \frac{1}{32}$

$\approx 1.5$

$18) \log (2.77\times {10}^{-4})$

$\approx -3.6$

$19) \ln 0.000062$

$\approx -9.7$

$20) \ln \mathrm{\pi }$

$\approx 1.1$

أمثل كلا من الاقترانات الآتية، وأحدد مجاله ومداه ومقطعيه الإحداثيين وخطوط تقاربه، وإن كان متزايدا أم متناقصا:

$21) f(x)= {\log }_5 x$

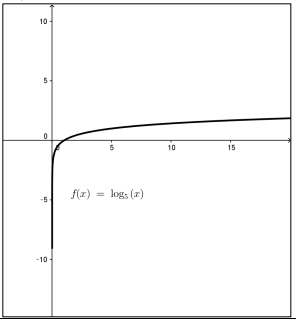
مجال: $\left(0,\infty \right)$

المدى: الأعداد الحقيقية R

الاقتران متزايد

ليس له مقطع y

مقطع x هو x=1

له خط تقارب رأسي هو محور y

$22) g(x)={\log }_{\frac{1}{4}} x$

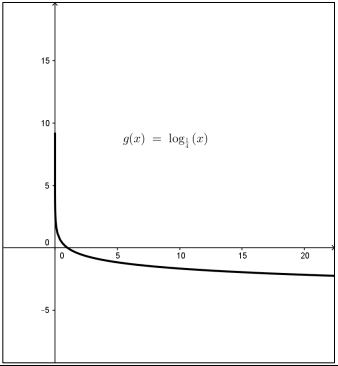
مجال: $\left(0,\infty \right)$

المدى: الأعداد الحقيقية R

الاقتران متناقص

ليس له مقطع y

مقطع x هو x=1

له خط تقارب رأسي هو محور y

$23) g(x)=\ln (x-1)$

 

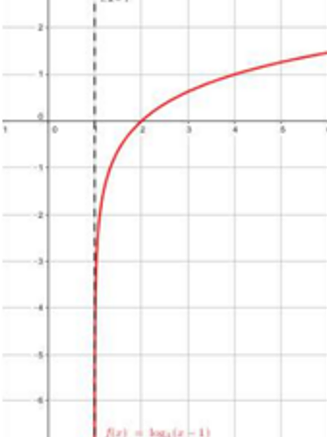
المجال: $\left(1,\infty \right)$

المدى: الأعداد الحقيقية R

الاقتران متزايد

ليس له مقطع y

مقطع x هو x=2

له خط تقارب رأسي هو x=1

$24) h(x)=8+5 \ln (2x+3)$

 

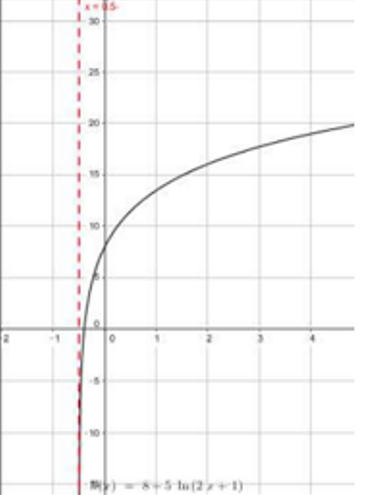
المجال: $\left(-0.5,\infty \right)$

المدى: الأعداد الحقيقية R

الاقتران متزايد

له مقطع y هو y=8

مقطع x هو x=-0.4

له خط تقارب رأسي هو x=-0.5

$25) f(x)=3-{\log }_4 (\frac{x}{2}-5)$

 

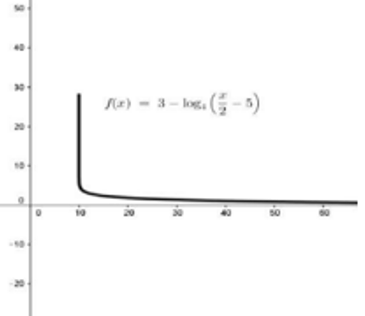
المجال: $\left(10,\infty \right)$

المدى: الأعداد الحقيقية R

الاقتران متناقص

ليس له مقطع y

ليس له مقطع x

له خط تقارب رأسي هو x=10

$26) w(x)=\left|\ln x\right|$

 

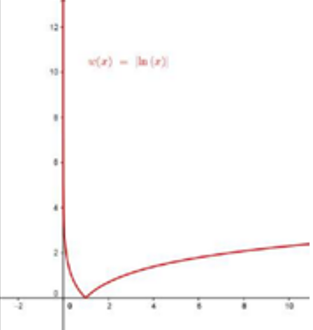
المجال: $\left(0,\infty \right)$

المدى: الأعداد الحقيقية R

الاقتران متناقص في الفترة (0,1) ومتزايد في الفترة $\left(1,\infty \right)$

ليس له مقطع y

مقطع x هو x=1

له خط تقارب رأسي هو محور y

النسيان: في تجربة لتحديد مدى تأثير المدة الزمنية في مدى تذكر الطلبة للمعلومات، عرضت مجموعة من الطلبة لاختبار في مادة معينة، وأعيد تعريضهم لاختبارات مكافئة لذلك الاختبار على فترات شهرية بعد ذلك. فوجد أن النسبة المئوية لمتوسط علامات الطلبة S(t)، بعد t شهرا تعطى  بالاقتران. $S\left(t\right)=78-15 \log (t+1) , t\ge 0$

27) أجد النسبة المئوية لمتوسط علامات الطلبة في بداية الدراسة.

$$\begin{gathered} s\left(t\right)=78-15 log (t+1) \\ s\left(0\right)=78-15 log 1=78 \end{gathered}$$

28) أجد النسبة المئوية لمتوسط علامات الطلبة بعد 4 أشهر من بدء الدراسة.

$s\left(4\right)=78-15 log \left(5\right)\approx 67.5$

29) أجد قيمة a التي تجعل منحنى الاقتران $f\left(x\right)={\log }_a x$ يمر بالنقطة (2,2)

$$\begin{gathered} f\left(x\right)=lo{g}_a x \\ 2=lo{g}_a 2 \\ {a}^2=2 \\ a=\sqrt{2} \end{gathered}$$

30) أجد قيمة c التي تجعل منحنى الاقتران $f\left(x\right)={\log }_c x$ يمر  بالنقطة $(\frac{1}{2},-4)$

$$\begin{gathered} f\left(x\right)=lo{g}_x x \\ -4=lo{g}_c \frac{1}{2} \\ {c}^{-4}=\frac{1}{2} \\ {c}^4=2 \\ c=2^{\frac{1}{4}} \end{gathered}$$

ضوء: تمثل المعادلة $A=2-\log 100T$ كمية الضوء التي تمتصها عينة من محلول A حيث T نسبة الضوء الذي ينتقل خلال المحلول (T نسبة شدة الضوء قبل اختراق المحلول $I_0$ إلى شدته  بعد اختراق المحلول I).

31) إذا كانت نسبة الضوء التي انتقلت خلال محلول %72؛ فأجد مقدار الضوء الذي امتصه المحلول.

$$\begin{gathered} A=2-log 100 T \\ A=2-log (100\times 0.72)\approx 0.143 \end{gathered}$$

32) إذا كانت كمية الضوء التي امتصها محلول 0.174؛ فأجد نسبة الضوء التي انتقلت خلاله

$$\begin{gathered} 0.174=2-log 100T \\ log 100T=2-0.174=1.826 \\ 100T={10}^{1.826} \\ T=\frac{{10}^{1.826}}{100}\approx 0.67 \end{gathered}$$

مهارات التفكير  العليا

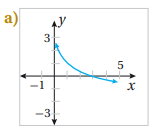
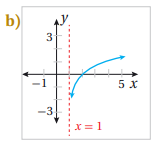
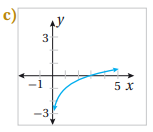
تبرير: أكتب بجانب كل اقتران مما يأتي، رمز التمثيل البياني المناسب له:

$33) f\left(x\right)={\log }_3 (x-1)$

التمثيل البياني له هو الرسم b لأن مجاله في الفترة $\left(1,\infty \right)$

$34) g(x)={\log }_3 \left(x\right)-1$

التمثيل البياني له هو الرسم c لأن مقطع x هو x=3 والاقتران متزايد

$35) h(x)=1-{\log }_3 \left(x\right)$

التمثيل البياني له هو الرسم a لأن مقطع x له هو x=3 والاقتران متناقص

 

 

 

36) تحد: أجد المقطع x للاقتران $f\left(x\right)=\log (x-k)$، حيث k ثابت.

$$\begin{gathered} 0=log (x-k) \\ x-k=1 \\ x=k+1 \end{gathered}$$

تبرير: أحدد إذا كانت الجمل الآتية صحيحة أم خطأ، وأبرر إجابتي بمثال:

37) يوجد قيود على مجال الاقترانات اللوغاريتمية دائما.

عبارة صحيحة لأن الاقتران اللوغاريتمي يجب أن يكون ما بداخله قيمة موجبة

38) لا يوجد قيود على مدى الاقترانات اللوغاريتمية.

عبارة صحيحة لأن مدى الاقتران اللوغاريتمي دائما الأعداد حقيقية

39) يوجد خط تقارب للتمثيل البياني للاقترانات اللوغاريتمية دائما.

عبارة صحيحة لأن مجال الاقتران يكون دائما محدد بنقطة بداية وتشكل خط التقارب الرأسي للاقتران

40) تبرير: من دون استعمال الآلة الحاسبة، أبين أي القيم الآتية أكبر. أبرر إجابتي:

${\log }_5 28 , {\log }_6 32 , {\log }_7 40$

$$\begin{gathered} lo{g}_5 28=h \\ {5}^h=28 \\ h>2 \\ lo{g}_6 32=y \\ {6}^y=32 \\ y<2 \\ lo{g}_7 40=z \\ {7}^z=40 \\ z<2 \end{gathered}$$

إذن الاقتران الأكبر هو $lo{g}_5 28$