رياضيات فصل أول

الاقترانات اللوغاريتمية

الاقتران اللوغاريتمي: هو الاقتران العكسي للاقتران الأسي $f\left(x\right)=b^x$ ويسمى الاقتران اللوغاريتمي للأساس b ويرمز له بالرمز ${\log }_b x$ ويقرأ لوغاريتم x للأساس b.

أي أن إذا كان $f\left(x\right)=b^x$ حيث $b>0 , b\ne 0 , x>0$ فإن $f^{-1}\left(x\right)={\log }_b x$.

العلاقة بين الصورتين الأسية واللوغاريتمية

إذا كان x >0 و $b>0 , b\ne 0$ فإن:

التحويل من الصورة اللوغاريتمية إلى الصورة الأسية:

 

التحويل من الصورة الأسية إلى الصورة اللوغاريتمية:

 

ملاحظة: اللوغاريتم هو أس حيث يمكنني إيجاد قيمة عبارات لوغاريتمية بسيطة باستعمال قوانين الأسس.

 

الخصائص الأساسية  للوغارتمات

إذا كان x >0 و $b>0 , b\ne 1$ فإن $\bullet {\log }_b 1=0 b^0=1\bullet {\log }_b b=1 b^1=b\bullet {\log }_b b^x=x b^x=b^x\bullet b^{{\log }_b x}=x , x>0 lo{g}_b x=lo{g}_b x$

 

اللوغاريتم الاعتيادي واللوغاريتم الطبيعي

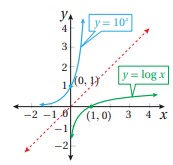
1) إذا كان أساس اللوغارتم هو 10 فنسمي اللوغاريتم باللوغاريتم الاعتيادي أو ${\log }_{10}$ وعادة يكتب بدون أساس حيث أن اللوغاريتم الاعتيادي $y=\log x$ هو الاقتران العكسي للاقتران الأسي $y={10}^x$، أي أن $y=\log x$، إذا وفقط إذا ${10}^y=x , x>0$.

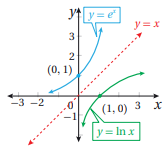
2) إذا كان أساس اللوغاريتم هو العدد النيبيري e فنسمي اللوغاريتم باللوغاريتم الطبيعي أو ln x حيث أن اللوغاريتم الطبيعي y=ln x هو الاقتران العكسي للاقتران الأسي الطبيعي $y=e^x$ أي أن y=ln x إذا وفقط إذا $e^y=x , x>0$

ملاحظة: 

1) خصائص اللوغاريتمات صحيحة للوغاريتم الاعتيادي واللوغاريتم الطبيعي

2) يمكننا إيجاد قيمة اللوغاريتم الاعتيادي باستخدام الآلة الحاسبة بالضغط على زر log ويمكننا إيجاد قيمة اللوغاريتم الطبيعي باستخدام الآلة الحاسبة بالضغط على زر ln.

 

تمثيل الاقتران اللوغاريتمي بيانيا

لتمثيل الاقتران اللوغاريتمي $y={\log }_b x$ بيانيا يمكننا استعمال العلاقة العكسية بين الاقتران اللوغارتمي والاقتران الأسي.

 

من خلال التمثيل البياني لبعض الاقترانات نتوصل إلى بعض خصائص الاقتران اللوغاريتمي:

خصائص الاقتران اللوغاريتمي

التمثيل البياني للاقتران اللوغاريتمي على الصورة $f\left(x\right)={\log }_b x$ حيث b عدد حقيقي و $b\ne 1 , b>0$ له الخصائص الآتية: 1) مجال الاقتران هو مجموعة الأعداد الحقيقية الموجبة $R^{+}$ أي الفترة $\left(0,\infty \right)$. 2) مدى الاقتران هو مجموعة الأعداد الحقيقية R. 3) يكون الاقتران متزايدا إذا كانت b>1 4) يكون الاقتران متناقصا إذا كانت $0<b<1$ 5) للاقتران خط تقارب رأسي هو المحور y. يقطع الاقتران المحور x في نقطة واحدة هي (1,0)، ولا يقطع المحور y.