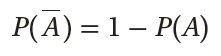رياضيات فصل ثاني

الاحتمالاتُ وأشكالُ فِنْ

أولًا : التعبيرُ بالرموزِ عنْ حوادثَ مُمثَّلةٍ بأشكالِ فِنْ

يُمكِنُ استعمالُ أشكالِ فِنْ للتعبيرِ عنْ حوادثِ تجربةٍ عشوائيةٍ بيانيًّا، وذلكَ لتسهيلِ إيجادِ احتمالاتِ هذهِ الحوادثِ.

فمثاً، إذا كانَ A و B حادثينِ في تجربةٍ عشوائيةٍ، فإنَّهُ يُمكِنُ تمثيلُهُما باستعمالِ أشكالِ فِنْ، وذلكَ برسمِ مستطيلٍ يُمثِّلُ الفضاءَ العينيَّ للتجربةِ،  ثمَّ رسمِ منحنى مُغلَقٍ يُمثِّلُ الحادثَ A ، ورسمِ منحنى آخرَ مُغلَقٍ يُمثِّلُ الحادثَ B.

 

 

 

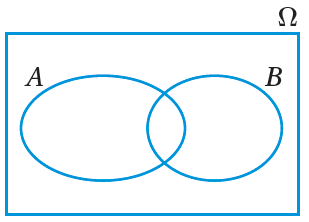
تُمثِّلُ المنطقةُ المُظلَّلةُ في شكلِ فِنْ المجاورِ تقاطعَ الحادثِ A والحادثِ B، ويُمكِنُ التعبيرُ عنْها بالرمزِ A∩B. أتعلَّمُ : تقاطعُ الحادثِ A والحادثِ B يعني وقوعَهُما معًا.

 

 

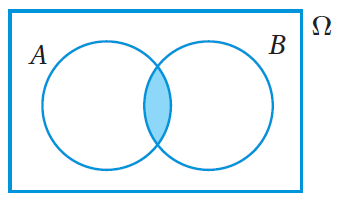
أمّا المنطقةُ المُظلَّلةُ في شكلِ فِنْ المجاورِ فتُمثِّلُ  اتحادَ الحادثِ A والحادثِ B، ويُمكِنُ التعبيرُ عنْها بالرمزِ  A∪B. أتعلَّمُ : اتحادُ الحادثِ A والحادثِ B يعني وقوعَ الحادثِ A، أوْ وقوعَ الحادثِ B، أوْ وقوعَ الحادثينِ معًا.

 

 

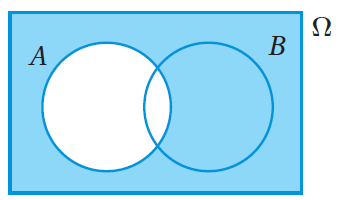
في حينِ تُمثِّلُ المنطقةُ المُظلَّلةُ في الشكلِ المجاورِالحادثَ المُتمِّمَ  (complement event)للحادثِ A، ويُمكِنُ التعبيرُ عنْهُ بالرمزِ $\overline{A}$

 

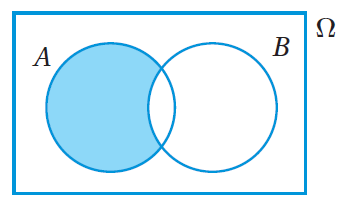
وأمّا الحادثُ الذي تُمثِّلُهُ المنطقةُ المُظلَّلةُ في الشكلِ المجاورِ فهوَ وقوعُ الحادثِ A فقطْ، وعدمُ وقوعِ الحادثِ B، ويُمكِنُ التعبيرُ عنْ هذا الحادثِ بالرمزِ A - B.

 

ثانيًا : إيجادُ احتمالاتِ حوادثَ لتجاربَ عشوائيةٍ مُمثَّلةٍ بأشكالِ فِنْ

تعلَّمْتُ سابقًا أنَّهُ إذا كانَتِ التجربةُ العشوائيةُ متساويةَ الاحتمالِ، فإنَّ احتمالَ وقوعِ أيِّ حادثٍ فيها يساوي نسبةَ عددِ عناصرِ الحادثِ إلى عددِ عناصرِ الفضاءِ العينيِّ.

بما أنَّ الفضاءَ العينيَّ Ω هوَ مجموعةٌ تحوي جميعَ النواتجِ التي يُتوقَّعُ حدوثُها عندَ إجراءِ تجربةٍ عشوائيةٍ ما، فإنَّ احتمالَ الفضاءِ

العينيِّ هوَ 1 ؛ أيْ إنَّ P(Ω) = 1 . ولهذا، فإنَّ احتمالَ الحادثِ المُتمِّمِ لأيِّ حادثٍ في الفضاءِ العينيِّ، مثلَ A ، هوَ 1 ناقصُ احتمالِ وقوعِ

الحادثِ A .

مفهومٌ أساسيٌّ (احتمالُ الحادثِ المُتمِّمِ)

بالكلماتِ: احتمالُ وقوعِ مُتمِّمةِ الحادثِ A هوُ 1 ناقصُ احتمالِ وقوعِ الحادثِ. بالرموزِ : لأيِّ حادثٍ(A) في تجربةٍ عشوائيةٍ، فإنَّ:

 

•• يُمكِنُ استعمالُ المفاهيمِ السابقةِ لإيجادِ احتمالاتِ حوادثَ مُمثَّلةٍ بأشكالِ فِنْ.

 

ثالثًا : الحوادثُ المتنافيةُ

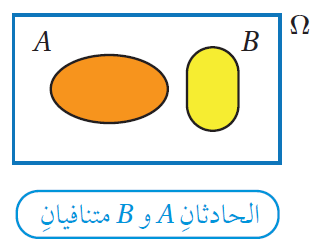
الحوادثُ المتنافيةُ (mutually exclusive events) : هيَ الحوادثُ التي لا يُمكِنُ وقوعُها معًا؛ ما يعني عدمَ وجودِ عناصرَ مشتركةٍ بينَها. فمثلًا ، عندَ رميِ حجرِ نردٍ مَرَّةً واحدةً، فإنَّ حادثَ ظهورِ العددِ 5 لا يُمكِنُ أنْ يقعَ معَ حادثِ ظهورِ العددِ 6 في الوقتِ نفسِهِ، وهذا يعني أنَّ تقاطعَهُما هوَ ∅، وأنَّ احتمالَ تقاطعِهِما هوَ صفرٌ.

 

الحوادثُ المتنافيةُ الشاملةُ
 

الحوادثُ الشاملةُ ( exhaustive events) هيَ الحوادثُ التي يُشكِّلُ اتحادُ نواتجِها المُحتمَلةِ الفضاءَ العينيَّ كاملًا. فمثلًا ، عندَ

إلقاءِ حجرِ نردٍ، فإنَّ حادثَ ظهورِ عددٍ أكبرَ منْ 3 وحادثَ ظهورِ عددٍ أقلَّ منْ 5 يُمثِّلانِ حادثينِ شاملينِ.
 

قدْ تكونُ بعضُ الحوادثِ متنافيةً وشاملةً. فمثلًا ، عندَ رميِ حجرِ نردٍ، فإنَّ حادثَ ظهورِ عددٍ فرديٍّ وحادثَ ظهورِ عددٍ زوجيٍّ

يُمثِّلانِ حادثينِ متنافيينِ؛ لأنَّهُ لا يُمكِنُ أنْ يقعا معًا. وهما أيضًا حادثانِ شاملانِ؛ لأنَّ نواتجَهُما المُحتمَلةَ تُشكِّلُ الفضاءَ

العينيَّ كاملًا.
 

يُظهِرُ شكلا فِنْ الآتيانِ كُلًّ منَ الحوادثِ المتنافيةِ، والحوادثِ الشاملةِ، والحوادثِ المتنافيةِ والشاملةِ :

 

•• إذا كانَتِ الحوادثُ متنافيةً وشاملةً، فإنَّ مجموعَ احتمالاتِها هوَ 1.

 

 

---

 

ورقة عمل درس الاحتمالاتُ وأشكالُ فِنْ

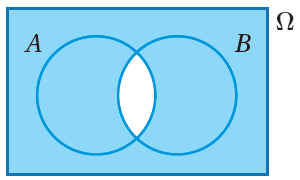
1) الرمز الذي يُعبر  عن الحادث الذي تُمثّله المنطقة المُظلَّلة في الشكل الآتي ، هو : 

$a) \overline{A\cup B} b) \overline{A}\cup B c) \overline{A\cap B} d) A-B$

 

الحل : 

أُلاحظ أنَّ المنطقة المُظلَّلة تُعبِّر عن عدم وقوع تقاطع للحادث  A والحادث B ؛ لذا يُمكِن

التعبير عن هذا الحادث بالرمز $\overline{A\cap B}$

---

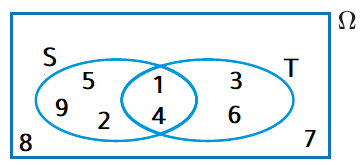
2) كُتِبَت الأعداد الصحيحة من 1 إلى 9 على مجموعة من البطاقات المُتطابقة، ثمّ اختيرَت بطاقة عشوائيًّا، ومُثّل الفضاء العينيُّ لهذه التجربة العشوائية التي تحوي الحادثين S و T في شكل فن التالي. فإنّ $P\left(\overline{S}\right)$ يساوي : 

 

$a) \frac{4}{9} b) \frac{5}{9} c) \frac{1}{3} d) \frac{2}{9}$

الحل : 

$\Omega = 9$    عدد عناصر S هو  5 عناصر 

$P\left(\overline{S}\right) = 1 - P\left(S\right) = 1 - \frac{5}{9} = \frac{4}{9}$

---

 

3) قرص دائري مُقسّم إلى 5 قطاعات غير مُتطابقة، ومُلوّنة بالألوان الأخضر والأصفر والأحمر والأزرق والبني . إذا كانَ الجدول المجاور يبين احتمال توقف المُؤشر عندَ كلّ لون من هذه الألوان ، ما احتمال توقف المؤشر عند اللون الأحمر؟ 

البني	الأزرق	الأحمر	الأصفر	الأخضر	اللون
0.08	0.3	3x	0.1	x	الاحتمال

 $a) 0.13 b) 0.52 c) 0.48 d) 0.39$

 

الحل : 

مجموعُ احتمالاتِ الحوادثِ المتنافيةِ والشاملةِ = 1

$x + 0.1 + 3x + 0.3 + 0.08 = 1 4x + 0.48 = 14x = 0.52x = 0.13$

احتمال اللون الأحمر  = 3x 

$3x = 3(0.13) = 0.39$

---

 

4) مُعتمِدًا شكلَ فِن الآتي الذي يُمثِّلُ الفضاء العينيَّ لتجربة عشوائية تحوي الحوادث : A ، و B، و C، و D، و E.   

فإنّ أحد الخيارات الآتية صحيحة :  

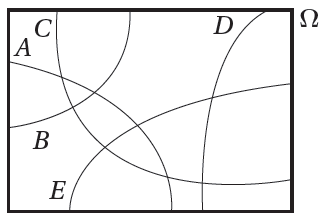
a) $C و A$  حادثان متنافيان.

b) $E و D$  حادثان شاملان .

c) $C و D و A$  حوادث متنافية وشاملة . 

d) $E و B و C و D و A$ حوادث شاملة.  

الحل : 

الاجابة الصحيحة (d) ؛ لأنّ اتحاد هذه الحوادث يساوي $\Omega$

---

 

5) سُئل 50 طالب عن هواياتهم المفضلة ، إذا كان 32 طالب يفضلون كرة القدم ، و 23 طالب يفضلون التنس ، و 18 طالب يفضلون كرة القدم والتنس.

a) مثل هذه البيانات بأشكال فن.

b) إذا اختير طالب عشوائيًّا ، فأجدُ احتمالَ أنْ يكونَ ممن يفضلون كرة القدم ، ولا يفضلون التنس . 

الحل :

a) مثل هذه البيانات بأشكال فن. 

أفترضُ أنَّ A هوَ حادثُ اختيارِ طالب يفضل كرة القدم ، وأنَّ B هوَ حادثُ اختيارِ  طالب يفضل التنس.

عدد الطلاب الذين يفضلون كرة القدم فقط : $32 - 18 = 14$ 

عدد الطلاب الذين يفضلون التنس فقط : $23 - 18 = 5$

عدد الطلاب الذين لا يفضلون كرة القدم ولا التنس : $50 -(14 + 5 + 18) = 13$

 

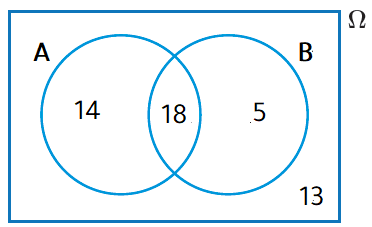
b) إذا اختير طالب عشوائيًّا ، فأجدُ احتمالَ أنْ يكونَ ممن يفضلون كرة القدم ، ولا يفضلون التنس . 

$P(A - B) = \frac{14}{50} = \frac{7}{25}$