تناولنا في الدرس السابق الية اشتقاق كثيرات الحدود وعلاقتها بالميل والسرعة المتوسطة .
تسمى النقطة التي يكون عندها ميل منحنى كثير الحدود صفرا، النقطة الحرجة
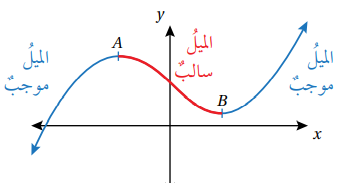
كما في الشكل المجاور A, B نقطتان حرجتان لان ميل المنحنى عند كل منهما صفر
- في النقطة d تسمى القيمة التي إشارة ميل المنحنى عن يسارها موجبة وعن يمينها سالبة القيمة العظمى المحلية لأنها أكبر من القيم المجاورة لها
- وتسمى القيمة h في النقطة -التي إشارة ميل المنحنى عن يسارها سالبة وعن يمينها موجبة القيمة الصغرى المحلية لأنها أصغر من القيم المجاورة لها.
مثال:
استعمل المشتقة لإيجاد القيم العظمى المحلية و القيم الصغرى المحلية للاقتران ( ان وجدت)
الخطوة 1
إذا توجد نقطتان حرجتان لمنحنى الاقتران x = 2, x = -2 لأن مشتقة الاقتران تساوي صفرا عند هاتين النقطتين
الخطوة 2
لتحديد اي النقاط الحرجة يوجد عندها قيمة عظمى او قيمة صغرى للاقتران نختبر اشارة ميل المنحنى حول كل منهما وذلك بتعويض بعض القيم القريبة منها .
|
X |
|
|
|
|
F ‘(x) |
1.23 |
0 |
|
|
إشارة الميل |
موجبة |
|
سالبة |
|
X |
1.9 |
2 |
2.1 |
|
F ‘(x) |
|
0 |
1.23 |
|
إشارة الميل |
سالبة |
|
موجبة |
تتغير اشارة ميل المنحنى حول X= -2 من موجبة الى سالبة لذا توجد قيمة محلية عظمى عندما X = -2 هي f(-2)=20 وتتغير اشارة ميل المنحنى حول x = 2 من سالبة الى موجبة لذا توجد قيمة محلية صغرى عندما x = 2 هي f(2) = -12
طريقة بديلة :
ممكن تمثيل الاقتران بيانيا ومن خلال التمثيل البياني نحدد القيمة العظمى و القيمة الصغرى فعند تمثيل الاقتران f(x) بيانيا فان النقطة تبدو أعلى من الناط المجاورة لها على المنحنى وبذلك تساوي القيمة العظمى 20 وتبدو النقطة هخفض من النقاط المجاورة لها و بذلك تساوي القيمة الصغرى 12-
- يمثل الاحداثي الصادي y للنقطة التي يتغير عندها اتجاه حركة الجسم من الصعود الى الهبوط قيمة عظمى لمنحنى المسافة - الزمن لان مشتقة المنحنى عند تلك النقطة تساوي صفرا ( المماس الافقي ) لذا يمكن استعمال المشتقة لتحديد النقطة التي يبلغ عندها الجسم اقصى ارتفاع .
مثال من الحياة
يمثل الاقتران ارتفاع كرة عن سطح الارض بالمتر بعد t ثانية من ركلها
1) أجد سرعة الكرة بعد 4 ثوان من ركلها
نشتق المسافة لتعطي السرعة
اذا سرعة الكرة بعد 4 ثوان هي
2) اجد اقصى ارتفاع تصله الكرة
لايجاد القيمةالعظمى نحدد القيم التي تحقق المعادلة h '(t) = 0
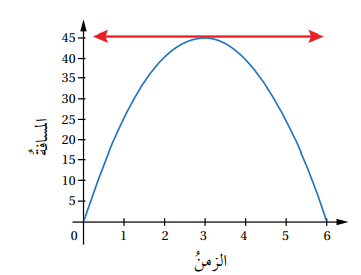
تتغير اشارة ميل المنحنى من موجبة الى سالبة لذا توجد قيمة عظمى عندما t = 3
اذا تصل الكرة اقصى ارتفاع عندما t= 3 وقيمة هذا الارتفاع هي
أقصى ارتفاع تصله الكرة 6m
مثال 3 : من الحياة
جدار : لدى مزارع 32m من السياج، أراد أن يسيج به حظيرة مستطيلة، طولها y مترًا، وعرضها x مترًا، بجانب جدار يكون أحد أضلاع هذه الحظيرة :
1 ) أبين أن الاقتران A(x) = x ( 32 - 2x ) يمثل مساحة الحظيرة .
طول السياج 32m؛ لذا فإن x+ y +x = 32
إذا ، طول الحظيرة y = 32 -2x
ومساحتها x( 32 -2 x ) مترًا مربعا .
2) أجد A'(X)
A(x) = x ( 32 - 2x )
A(x) = 32x - 2x2
A'(x) = 32 - 4x
3) استعمل المشتقة لإيجاد قيمة x التي تجعل مساحة الحظيرة أكبر ما يمكن .
لإيجاد قيمة x، أحل المعادلة A'(x) = 0
32 -4x = 0
32 = 4x
x = 8
نعوض قيمة x= 8 بالاقتران A(x)
A(8 ) = 8 ( 32 - 2(8) ) = 128
إذا أكبر مساحة ممكنة للحظيرة 128m2 وهي تنتج عندما يكون عرض الحظيرة 8m ، وطولها 16m