

أجد مشتقة كل اقتران مما يأتي :

أجد مشتقة كل اقتران مما يأتي :

أجد مشتقة كل اقتران مما يأتي :

a) أجد ميل المماس لمنحنى الاقتران عندما :
b) أجد ميل العمودي على المماس لمنحنى الاقتران عندما :

قيمة بدل الخدمة لأحد المُنتّجات تُحسَب بالدينار, باستعمال الاقتران: ، حيث x عدد القطع المبيعة من المنتج .
a) أجد مُعدّل تغيُّر قيمة بدل الخدمة بالنسبة إلى عدد القطع المبيعة من المُنتج.
b) أجد مُفْسَرًا معنى الناتج .

أجد مشتقة كل اقتران مما يأتي :

أجد مشتقة كل اقتران مما يأتي:

أجد معادلة مماس منحنى المعادلة الوسيطية الآتية عندما :

أجد مشتقة كل اقتران مما يأتي:
أجد معادلة المماس لكل اقتران مما يأتي عند قيمة المعطاة
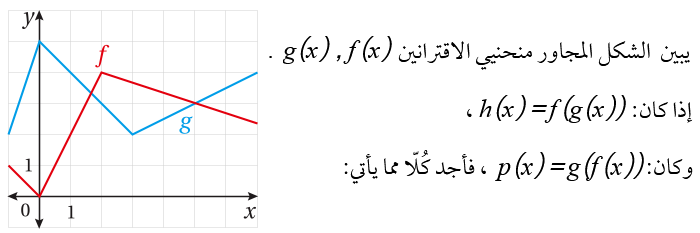
23) إذا كان ، ، وكان ، فأجد ؟
24) إذا كان ، فأثبت أنَّ
بكتيريا: يُمثَّل الاقتران: عدد الخلايا البكتيرية بعد t ساعة في مجتمع بكتيري:
25) أجد مُعدل نمو المجتمع بعد 3 ساعات بدلالة الثابت N .
26) إذا كان مُعدِّل نمو المجتمع بعد k ساعة هو 0.2 خلية لكل ساعة ، فما قيمة k بدلالة الثابت؟
أجد المشتقة العليا المطلوبة في كل ممَّا يأتي:
30) إذا كان الاقتران: فأجد ميل مماس منحنى الاقتران عند النقطة .
31) مواد ُمشِعّة: يُمكِن نمذجة الكمية A (بالغرام) المتبقية من عيَّنةٍ كتلتها الابتدائية من عنصر البلوتونيوم بعد t يومًا باستعمال الاقتران: . أجد مُعدِّل تحلل عنصر البلوتونيوم عندما .
زنبرك: تتحرّك كرة مُعلِّقة بزنبرك إلى الأعلى وإلى الأسفل. ويُحدد الاقتران: :موقع الكرة عند أي زمن لاحق ، حيث t الزمن بالثواني ،
و S الموقع بالسنتيمترات:
32) أجد السرعة للكرة عندما .
33) أجد موقع الكرة عندما تكون سرعتها صفرًا.
34) أجد موقع الكرة عندما يكون تسارعها صفرًا.
أجد معادلة المماس لمنحنى كل معادلة وسيطية ممّا يأتي عند النقطة المُحدّدة بقيمة t المعطاة:
39) يعطى منحنى بالمعادلة الوسيطية: ، حيث . أثبت أن ميل المماس وميل العمودي على المماس
لمنحنى هذه العلاقة عندما ، هما على الترتيب.

تبرير: إذا كان الاقتران: ، حيث a ,b ثابتان موجبان. وكان ميل المماس لمنحنى الاقتران عند النقطة P هو 1 .
فأجيب عن السؤالين الآتيين تباعًا:
42) أثبت أنَ الإحداثي للنقطة P أقل من 1 .
43) أجد قيمة كل من ، علمًا بأنَ هي النقطة .ثم أبرّر إجابتي.
44) أجد إحداثيي النقطة التي يكون عندها ميل المماس .
تبرير: يعطى منحنى بالمعادلة الوسيطية :
45) أجد بدلالة t .
46) أجد معادلة العمودي على مماس المنحنى عند النقطة
47) أثبت أن مساحة المثلث المُكوَّن من العمودي على المماس ، والمحورين الإحداثيين ، هي .
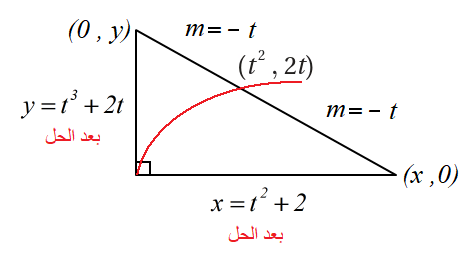
سنجد مقطعي العمودي على المماس والمحورين الإحداثيين :
تحدّ: أجد لكل مما يأتي:
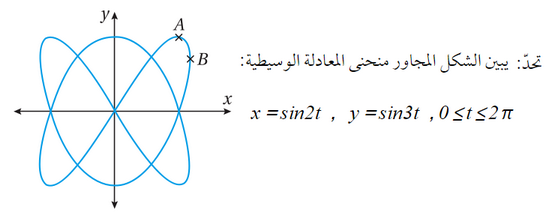
50) إذا كان مماس منحنى المعادلة أفقيًّا عند النقطة A الواقعة في الربع الأوّل ، فأجد إحداثيي A .
51) إذا كان مماس المنحنى موازيًا للمحور Y عند النقطة A فأجد إحداثيي B .
52) إذا مرَّ فرعان من المنحنى بنقطة الأصل كما هو مُوضّح في الشكل، فأجد ميل المماس لكل منهما عند هذه النقطة.
تبرير: يمثل الاقتران: موقع جُسَيْم يتحرَّك في مسار مستقيم؛ حيث s الموقع بالأمتار، و t الزمن بالثواني:
53) أجد سرعة الجُسَيُم وتسارعه بعد t ثانية.
54) أجد موقع الجُسَيْم وتسارعه عندما تكون سرعته صفرًا.
55) متى يعود الجُسَيْم إلى موقعه الابتدائي؟













