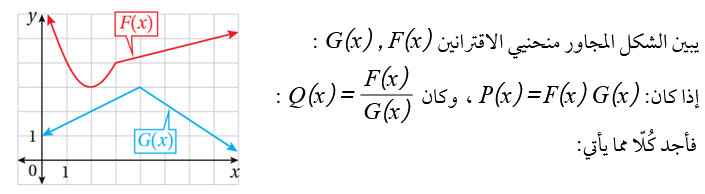رياضيات فصل أول

التوجيهي علمي

الشرح الملخص أوراق العمل حل اسئلة الدرس النتاجات

أجد مشتقة كل اقتران مما يأتي:

$a) f (x) = (x^{3} - 2 x^{2} + 3) (7 x^{2} - 4 x) S o l u t i o n : f^{'} (x) = \frac{d}{d x} (x^{3} - 2 x^{2} + 3) (7 x^{2} - 4 x) + (x^{3} - 2 x^{2} + 3) \frac{d}{d x} (7 x^{2} - 4 x) = (3 x^{2} - 4 x) (7 x^{2} - 4 x) + (x^{3} - 2 x^{2} + 3) (14 x - 4) = 35 x^{4} - 72 x^{3} + 24 x^{2} + 42 x - 12$

$b) f (x) = l n x c o s x S o l u t i o n : f^{'} (x) = \frac{d}{d x} (l n x) c o s x + l n x \frac{d}{d x} (c o s x) = \frac{1}{x} c o s x - l n x s i n x f^{'} (x) = \frac{c o s x}{x} - l n x s i n x$

أجد مشتقة كل اقتران مما يأتي:

$a) f (x) = \frac{x + 1}{2 x + 1} S o l u t i o n : f^{'} (x) = \frac{\frac{d}{d x} (x + 1) (2 x + 1) - (x + 1) \frac{d}{d x} (2 x + 1)}{{(2 x + 1)}^{2}} f^{'} (x) = \frac{(1) (2 x + 1) - (x + 1) (2)}{{(2 x + 1)}^{2}} = \frac{- 1}{{(2 x + 1)}^{2}}$

$b) f (x) = \frac{s i n x}{e^{x}} S o l u t i o n : f^{'} (x) = \frac{\frac{d}{d x} (s i n x) e^{x} - s i n x \frac{d}{d x} (e^{x})}{e^{2 x}} = \frac{(c o s x) e^{x} - s i n x (e^{x})}{e^{2 x}} = \frac{c o s x - s i n x}{e^{x}}$

سكان: يعطى عدد سكان مدينة صغيرة بالاقتران: $P (t) = \frac{500 t^{2}}{2 t + 9}$

حيث t الزمن بالسنوات ، و P عدد السكّان بالآلاف:

a) أجد مُعدِّل تغيُّر عدد السكّان في المدينة بالنسبة إلى الزمن.

$S o l u t i o n : P^{'} (t) = \frac{\frac{d}{d x} (500 t^{2}) (2 t + 9) - (500 t^{2}) \frac{d}{d x} (2 t + 9)}{{(2 t + 9)}^{2}} = \frac{(1000 t) (2 t + 9) - (500 t^{2}) (2)}{{(2 t + 9)}^{2}} = \frac{1000 t^{2} + 9000 t}{{(2 t + 9)}^{2}}$

b) أجد مُعدِّل تغيِّرْ عدد السكّان في المدينة عندما $t = 12$ مُفْسَّرًا معنى الناتج.

$S o l u t i o n : P^{'} (12) = \frac{1000 {(12)}^{2} + 9000 (12)}{{(2 (12) + 9)}^{2}} = 231.4$

أجد مشتقة كل اقتران مما يأتي:

$a) f (x) = \frac{1}{5 x - x^{2}} S o l u t i o n : f^{'} (x) = \frac{- \frac{d}{d x} (5 x - x^{2})}{{(5 x - x^{2})}^{2}} = \frac{2 x - 5}{{(5 x - x^{2})}^{2}}$

$b) f (x) = \frac{1}{e^{x} + \sqrt{x}} S o l u t i o n : f' (x) = \frac{- \frac{d}{d x} (e^{x} + \sqrt{x})}{{(e^{x} + \sqrt{x})}^{2}} = \frac{- e^{x} - \frac{1}{2 \sqrt{x}}}{{(e^{x} + \sqrt{x})}^{2}} = - \frac{2 \sqrt{x} e^{x} + 1}{2 \sqrt{x} {(e^{x} + \sqrt{x})}^{2}}$

أجد مشتقة كل اقتران مما يأتي:

$a) f (x) = x c o t x S o l u t i o n : f^{'} (x) = \frac{d}{d x} (x) c o t x + x \frac{d}{d x} (c o t x) = c o t x - x c s c^{2} x$

$b) f (x) = \frac{t a n x}{1 + s i n x} S o l u t i o n : f^{'} (x) = \frac{\frac{d}{d x} (t a n x) (1 + s i n x) - t a n x \frac{d}{d x} (1 + s i n x)}{{(1 + s i n x)}^{2}} = \frac{(s e c^{2} x) (1 + s i n x) - t a n x (c o s x)}{{(1 + s i n x)}^{2}}$

أجد المشتقات الثلاث الأولى للاقتران: $f (x) = x s i n x$

$S o l u t i o n : f^{'} (x) = \frac{d}{d x} (s i n x) x + s i n x \frac{d}{d x} (x) = x c o s x + s i n x f^{''} (x) = \frac{d}{d x} (c o s x) x + c o s x \frac{d}{d x} (x) + \frac{d}{d x} (\sin x) = - x \sin x + \cos x + \cos x = - x \sin x + 2 \cos x f^{'''} (x) = - x c o s x - s i n x - 2 \sin x = - x c o s x - 3 \sin x$

أجد مشتقة كل اقتران مما يأتي:

$1) f (x) = \frac{x^{3}}{2 x - 1} S o l u t i o n : f^{'} (x) = \frac{3 x^{2} (2 x - 1) - 2 (x^{3})}{{(2 x - 1)}^{2}} = \frac{4 x^{3} - 3 x^{2}}{{(2 x - 1)}^{2}}$

$2) f (x) = x^{3} s e c x S o l u t i o n : f^{'} (x) = 3 x^{2} s e c x + x^{3} s e c x t a n x$

$3) f (x) = \frac{x + 1}{c o s x} S o l u t i o n : f^{'} (x) = \frac{c o s x + (x + 1) s i n x}{c o s^{2} x}$

$4) f (x) = e^{x} (t a n x - x) S o l u t i o n : f^{'} (x) = e^{x} (t a n x - x) + e^{x} (s e c^{2} x - 1) = e^{x} (t a n x - x + s e c^{2} x - 1)$

$5) f (x) = \frac{s i n x + c o s x}{e^{x}} S o l u t i o n : f^{'} (x) = \frac{e^{x} (c o s x - s i n x) - e^{x} (s i n x + c o s x)}{e^{2 x}} = \frac{e^{x} c o s x - e^{x} s i n x - e^{x} s i n x - e^{x} c o s x}{e^{2 x}} = - 2 \frac{s i n x}{e^{x}}$

$6) f (x) = x^{3} s i n x + x^{2} c o s x S o l u t i o n : f^{'} (x) = 3 x^{2} s i n x + x^{3} c o s x + 2 x c o s x - x^{2} s i n x = 2 x^{2} s i n x + x^{3} c o s x + 2 x c o s x$

$7) f (x) = \sqrt[3]{x} (\sqrt{x} + 3) S o l u t i o n : f (x) = x^{\frac{5}{6}} + 3 x^{\frac{1}{3}} f^{'} (x) = \frac{5}{6} x^{\frac{- 1}{6}} + x^{\frac{- 2}{3}} = \frac{5}{6 \sqrt[6]{x}} + \frac{1}{\sqrt[3]{x^{2}}}$

$8) f (x) = \frac{1 + s e c x}{1 - s e c x} S o l u t i o n : f^{'} (x) = \frac{s e c x t a n x (1 - s e c x) + s e c x t a n x (1 + s e c x)}{{(1 - s e c x)}^{2}} = \frac{2 s e c x t a n x - s e c^{2} x t a n x + s e c^{2} x t a n x}{{(1 - s e c x)}^{2}} = \frac{2 s e c x t a n x}{{(1 - s e c x)}^{2}}$

$9) f (x) = \frac{2 - \frac{1}{x}}{x - 3} S o l u t i o n : f (x) = \frac{2 x - 1}{x^{2} - 3 x} f^{'} (x) = \frac{2 (x^{2} - 3 x) - (2 x - 1) (2 x - 3)}{{(x^{2} - 3 x)}^{2}} = - \frac{2 x^{2} - 2 x + 3}{{(x^{2} - 3 x)}^{2}}$

$10) f (x) = (x^{3} - x) (x^{2} + 2) (x^{2} + x + 1) S o l u t i o n : \frac{d}{d x} (f \times g \times h) = \frac{d}{d x} (f) \times g \times h + f \times \frac{d}{d x} (g) \times h + f \times g \times \frac{d}{d x} (h) f^{'} (x) = (3 x^{2} - 1) (x^{2} + 2) (x^{2} + x + 1) + (x^{3} - x) (2 x) (x^{2} + x + 1) + (x^{3} - x)) (x^{2} + 2) (2 x + 1) = 7 x^{6} + 6 x^{5} + 10 x^{4} + 4 x^{3} - 3 x^{2} - 4 x - 2$

$11) f (x) = {(c s c x + c o t x)}^{- 1} S o l u t i o n : f (x) = \frac{1}{c s c x + c o t x} f^{'} (x) = - \frac{\frac{d}{d x} (c s c x) + \frac{d}{d x} (c o t x)}{{(c s c x + c o t x)}^{2}} = - \frac{(- c s c x c o t x - c s c^{2} x)}{{(c s c x + c o t x)}^{2}} = \frac{c s c x c o t x + c s c^{2} x}{{(c s c x + c o t x)}^{2}} = \frac{c s c x (c o t x + c s c x)}{{(c s c x + c o t x)}^{2}} = \frac{c s c x}{c s c x + c o t x}$

إذا كان $g (x), f (x)$ اقترانين قابلين للاشتقاق عندما $x = 0$ ، وكان

$f (0) = 5, f^{'} (0) = - 3, g (0) = - 1, g^{'} (0) = 2$ ، فأجد كُلّا ممَا يأتي:

$12) {(f \times g)}^{'} (0) S o l u t i o n : {(f \times g)}^{'} (0) = f' (0) \times g (0) + f (0) \times g' (0) = - 3 \times - 1 + 5 \times 2 = 3 + 10 = 13$

$13) (\frac{f}{g})' (0) S o l u t i o n : {(\frac{f}{g})}^{'} (0) = \frac{f^{'} (0) \times g (0) - f (0) \times g^{'} (0)}{g^{2} (0)} = \frac{- 3 \times - 1 - 5 \times 2}{{(- 1)}^{2}} = - 7$

$14) (7 f - 2 f g)' (0) S o l u t i o n : {(7 f - 2 f g)}^{'} (0) = 7 \times - 3 - 2 (13) = - 21 - 26 = - 47$

أجد المشتقة الثانية لكل اقتران مما يأتي عند قيمة $x$ المعطاة:

$15) f (x) = \frac{x^{2} - 4}{x^{2} + 4}, x = - 2 S o l u t i o n : f (x) = 1 - \frac{8}{x^{2} + 4} f^{'} (x) = \frac{16 x}{{(x^{2} + 4)}^{2}} f^{''} (x) = \frac{16 {(x^{2} + 4)}^{2} - 16 x (2 ((x^{2} + 4) 2 x)}{{(x^{2} + 4)}^{4}} = - \frac{16 (3 x^{2} - 4)}{(x^{2} + 4) 3} f^{''} (- 2) = - \frac{16 (3 {(- 2)}^{2} - 4)}{({(- 2)}^{2} + 4) 3} = - \frac{1}{4}$

$16) f (x) = \frac{1 + x}{1 + \sqrt[3]{x}}, x = 8 S o l u t i o n : f (x) = \frac{(1 + \sqrt[3]{x}) (1 - x^{\frac{1}{3}} + x^{\frac{2}{3}})}{1 + \sqrt[3]{x}} = (1 - x^{\frac{1}{3}} + x^{\frac{2}{3}}) f^{'} (x) = - \frac{1}{3} x^{\frac{- 2}{3}} + \frac{2}{3} x^{\frac{- 1}{3}} f^{''} (x) = \frac{2}{9} x^{\frac{- 5}{3}} - \frac{2}{9} x^{\frac{- 4}{3}} f^{''} (8) = \frac{2}{9} {(8)}^{\frac{- 5}{3}} - \frac{2}{9} {(8)}^{\frac{- 4}{3}} = \frac{2}{9 (32)} - \frac{2}{9 (16)} = \frac{1}{9 (16)} - \frac{2}{9 (16)} = - \frac{1}{144}$

$17) f (x) = \frac{1 - x}{1 + \sqrt{x}}, x = 4 S o l u t i o n : f (x) = \frac{(1 + \sqrt{x}) (1 - \sqrt{x})}{1 + \sqrt{x}} = 1 - \sqrt{x} f (x) = 1 - x^{\frac{1}{2}} f^{'} (x) = - \frac{1}{2} x^{\frac{- 1}{2}} f^{''} (x) = \frac{1}{4} x^{\frac{- 3}{2}} f^{''} (4) = \frac{1}{4} {(4)}^{\frac{- 3}{2}} = \frac{1}{32}$

أجد معادلة المماس لكل اقتران مما يأتي عند النقطة المعطاة:

$18) f (x) = \frac{1 + x}{1 + e^{x}}, (0, \frac{1}{2}) m = f^{'} (x) = \frac{1 (1 + e^{x}) - e^{x} (1 + x)}{{(1 + e^{x})}^{2}} = - \frac{x e^{x} - 1}{{(1 + e^{x})}^{2}} f^{'} (0) = - \frac{(0) e^{0} - 1}{{(1 + e^{0})}^{2}} = \frac{1}{4}; e^{0} = 1 y - y_{1} = m (x - x_{1}); m = \frac{1}{4}, x_{1} = 0, y_{1} = \frac{1}{2} y - \frac{1}{2} = \frac{1}{4} (x - 0) \Rightarrow y = \frac{1}{4} x + \frac{1}{2}$

$19) f (x) = e^{x} c o s x + s i n x, (0, 1) S o l u t i o n : m = f^{'} (x) = e^{x} c o s x - e^{x} s i n x + c o s x f^{'} (0) = e^{0} c o s (0) - e^{0} s i n (0) + c o s (0) = 2; e^{0} = 1 y - y_{1} = m (x - x_{1}); m = 2, x_{1} = 0, y_{1} = 1 y - 1 = 2 (x - 0) \Rightarrow y = 2 x + 1$

أثبت صحة كلً ممَّا يأتي معتمدًا أن : $\frac{d}{d x} (s i n x) = c o s x, \frac{d}{d x} (c o s x) = - c o s x$

$20) \frac{d}{d x} (c o t x) = - c s c^{2} x S o l u t i o n : c o t x = \frac{c o s x}{s i n x} \frac{d}{d x} (c o t x) = \frac{d}{d x} (\frac{c o s x}{s i n x}) = \frac{\frac{d}{d x} (c o s x) s i n x - c o s x \frac{d}{d x} (s i n x)}{s i n^{2} x} = \frac{(- s i n x) s i n x - c o s x (c o s x)}{s i n^{2} x} = - \frac{s i n^{2} x + c o s^{2} x}{s i n^{2} x}; s i n^{2} x + c o s^{2} x = 1 = - \frac{1}{s i n^{2} x}; c s c x = \frac{1}{s i n x} = - c s c^{2} x$

$21) \frac{d}{d x} (s e c x) = s e c x t a n x S o l u t i o n : c s c x = \frac{1}{c o s x} \frac{d}{d x} (s e c x) = \frac{d}{d x} (\frac{1}{c o s x}) = - \frac{\frac{d}{d x} (c o s x)}{c o s^{2} x} = - \frac{- s i n x}{c o s^{2} x} = \frac{1}{c o s x} \times \frac{s i n x}{c o s x} = s e c x t a n x$

$22) \frac{d}{d x} (c s c x) = - c s c x c o t x S o l u t i o n : c s c x = \frac{1}{s i n x} \frac{d}{d x} (c s c x) = \frac{d}{d x} (\frac{1}{s i n x}) = - \frac{\frac{d}{d x} (s i n x)}{s i n^{2} x} = - \frac{c o s x}{s i n^{2} x} = - \frac{1}{s i n x} \times \frac{c o s x}{s i n x} = - c s c x c o t x$

ألاحظ المشتقة المعطاة في كل مما يأتي ، ثم أجد المشتقة العليا المطلوبة:

$23) f^{''} (x) = 2 - \frac{2}{x}, f^{'''} (x) S o l u t i o n : f^{''} (x) = 2 - \frac{2}{x} f^{'''} (x) = 0 - \frac{- 2}{x^{2}} = \frac{2}{x^{2}}$

$24) f^{'''} (x) = 2 \sqrt{x}, f^{(4)} (x) S o l u t i o n : f^{'''} (x) = 2 \sqrt{x} f^{(4)} (x) = 2 \frac{1}{2 \sqrt{x}} = \frac{1}{\sqrt{x}}$

$25) f^{(4)} (x) = 2 x + 1, f^{(6)} (x) S o l u t i o n : f^{(4)} (x) = 2 x + 1 f^{(5)} (x) = 2 f^{(6)} (x) = 0$

26) نباتات هجينة: وجد باحثون زراعيون أنه يمكن التعبير عن ارتفاع نبتة مُهجّنة من نبات

تبَّاع الشمس $h$ بالأمتار ، باستعمال الاقتران $h (t) = \frac{3 t^{2}}{4 + t^{2}}$ ، حيث t الزمن بالأشهر

بعد زراعة البذور. أجد مُعدِّل تغيُر ارتفاع النبتة بالنسبة إلى الزمن.

$S o l u t i o n : h^{'} (t) = \frac{\frac{d}{d x} (3 t^{2}) (4 + t^{2}) - (3 t^{2}) \frac{d}{d x} (4 + t^{2})}{{(4 + t^{2})}^{2}} = \frac{(6 t) (4 + t^{2}) - (3 t^{2}) (2 t)}{{(4 + t^{2})}^{2}} h^{'} (t) = \frac{24 t + 6 t^{3} - 6 t^{3}}{{(4 + t^{2})}^{2}} = \frac{24 t}{{(4 + t^{2})}^{2}}$

إذا كان الاقتران: $y = e^{x} s i n x$ ، فأجيب عن السؤالين الآتيين تباعًا:

$27) \frac{d^{2} y}{d x^{2}}, \frac{d y}{d x} S o l u t i o n : y = e^{x} s i n x \frac{d y}{d x} = \frac{d}{d x} (e^{x}) s i n x + e^{x} \frac{d}{d x} (s i n x) = e^{x} s i n x + e^{x} c o s x = e^{x} (s i n x + c o s x) ∴ \frac{d y}{d x} = e^{x} (s i n x + c o s x) \frac{d^{2} y}{d x^{2}} = \frac{d}{d x} (e^{x}) (s i n x + c o s x) + e^{x} \frac{d}{d x} (s i n x + c o s x) = (e^{x}) (s i n x + c o s x) + e^{x} (c o s x - s i n x) = e^{x} s i n x + e^{x} c o s x + e^{x} c o s x - e^{x} s i n x = 2 e^{x} c o s x ∴ \frac{d^{2} y}{d x^{2}} = 2 e^{x} c o s x$

28) أُثبتُ أنّ $\frac{d^{2} y}{d x^{2}} = 2 \frac{d y}{d x} - 2 y$

$S o l u t i o n : y = e^{x} s i n x \Rightarrow - 2 y = - 2 e^{x} s i n x . . . . 1 \frac{d y}{d x} = e^{x} s i n x + e^{x} c o s x \Rightarrow 2 \frac{d y}{d x} = 2 e^{x} s i n x + 2 e^{x} c o s x . . . . 2 1 + 2 = - 2 e^{x} s i n x + 2 e^{x} s i n x + 2 e^{x} c o s x = 2 e^{x} c o s x = \frac{d^{2} y}{d x^{2}} \Rightarrow \frac{d^{2} y}{d x^{2}} = 2 \frac{d y}{d x} - 2 y$

29) أثبت أن $h = r (c s c θ - 1)$

من المثلث القائم الظاهر في الشكل نجد أنَّ:

$S o l u t i o n : s i n θ = \frac{r}{r + h} \Rightarrow \frac{1}{s i n θ} = \frac{r + h}{r}; \frac{1}{s i n θ} = c s c θ \Rightarrow c s c θ = \frac{r + h}{r} \Rightarrow r c s c θ = r + h \Rightarrow r c s c θ - r = h \Rightarrow r (c s c θ - 1) = h$

30) أجد معدل تغيّر h ‏ بالنسبة إلى $θ$ عندما $θ = \frac{π}{6}$ (أفترض أن $r = 6371 k m$ ).

$S o l u t i o n : h (θ) = r (c s c θ - 1) h^{'} (θ) = - r c s c θ c o t θ h^{'} (\frac{π}{6}) = - (6371) c s c (\frac{π}{6}) c o t (\frac{π}{6}) = - 12742 \sqrt{3}$

31) إذا كان: $f (x) = 9 l n x + \frac{1}{2 x^{2}}$ ، فأثبت أن : $f^{'} (x) = \frac{(3 x - 1) (3 x + 1)}{x^{3}}$

$S o l u t i o n : f^{'} (x) = \frac{9}{x} - \frac{\frac{d}{d x} (2 x^{2})}{{(2 x^{2})}^{2}} = \frac{9}{x} - \frac{4 x}{4 x^{4}} = = \frac{9}{x} - \frac{1}{x^{3}} = \frac{9 x^{2} - 1}{x^{3}}; x^{2} - y^{2} = (x - y) (x + y) = \frac{(3 x - 1) (3 x + 1)}{x^{3}}$

$32) P^{'} (2) S o l u t i o n : P (x) = F (x) G (x) P^{'} (x) = F^{'} (x) G (x) + F (x) G^{'} (x) P^{'} (2) = F^{'} (2) G (2) + F (2) G^{'} (2); F (2) = 3, F^{'} (2) = 0 a n d G (2) = 2, G^{'} (2) = \frac{1}{2} P^{'} (2) = (0) \times (2) + (3) \times \frac{1}{2} = \frac{3}{2}$

$33) Q^{'} (7) S o l u t i o n : Q (x) = \frac{F (x)}{G (x)} Q^{'} (x) = \frac{F^{'} (x) G (x) - F (x) G^{'} (x)}{G^{2} (x)} Q^{'} (7) = \frac{F^{'} (7) G (7) - F (7) G^{'} (7)}{G^{2} (7)}; F (7) = 5, F^{'} (7) = \frac{1}{4} a n d G (7) = 1, G^{'} (7) = - \frac{2}{3} Q^{'} (7) = \frac{(\frac{1}{4}) (1) - (5) (- \frac{2}{3})}{{(1)}^{2}} = \frac{43}{12}$

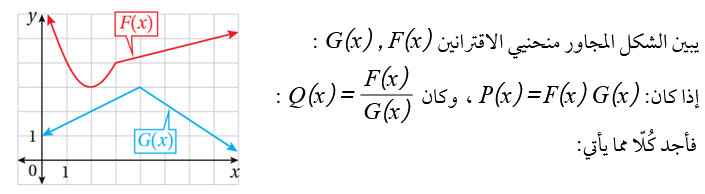
تبرير: إذا كان: $y = \frac{1 - e^{- x}}{1 + e^{- x}}$ ، فأجيب عن السؤالين الآتيين تباعًا:

34) أجد ميل المماس عند نقطة الأصل.

$S o l u t i o n : m = \frac{d y}{d x}; x_{1} = 0, y_{1} = 0 \frac{d y}{d x} = \frac{\frac{d}{d x} (1 - e^{- x}) (1 + e^{- x}) - (1 - e^{- x}) \frac{d}{d x} (1 + e^{- x})}{{(1 + e^{- x})}^{2}} \frac{d y}{d x} = \frac{(e^{- x}) (1 + e^{- x}) - (1 - e^{- x}) (- e^{- x})}{{(1 + e^{- x})}^{2}} = \frac{2 e^{x}}{{(1 + e^{x})}^{2}}; w h e n x = 0, e^{0} = 1 = \frac{2 e^{0}}{{(1 + e^{0})}^{2}} = \frac{2}{4} = \frac{1}{2} m = \frac{1}{2}, x_{1} = 0, y_{1} = 0 y - y_{1} = m (x - x_{1}) y - 0 = \frac{1}{2} (x - 0) \Rightarrow y = \frac{1}{2} x$

35) أبين عدم وجود مماس أفقي للاقتران مبُرَّرًا إجابتي.

$S o l u t i o n : \frac{d y}{d x} = \frac{(e^{- x}) (1 + e^{- x}) - (1 - e^{- x}) (- e^{- x})}{{(1 + e^{- x})}^{2}} = 0 \Rightarrow (e^{- x}) (1 + e^{- x}) + (1 - e^{- x}) (e^{- x}) = 0; d i v i d e d b y e^{- x} \Rightarrow 1 + e^{- x} + 1 - e^{- x} = 0 \Rightarrow 2 = 0!!! 2 \neq 0$

تحدّ: إذا كان: $y = \frac{x + 1}{x - 1}$ ، حيث: $x \neq 1$ ، فأجيب عن الأسئلة الثلاثة الآتية تباعًا:

$36) \frac{d y}{d x} = ? S o l u t i o n : y = \frac{x + 1}{x - 1} = 1 + \frac{2}{x - 1} \frac{d y}{d x} = - \frac{2}{{(x - 1)}^{2}}$

37) أعيد كتابة المعادلة بالنسبة إلى المُتغيَر $x$ ( $x$ اقتران بالنسبة إلى $y$ ) ثم أجد $\frac{d x}{d y}$ .

$S o l u t i o n : y = \frac{x + 1}{x - 1} = 1 + \frac{2}{x - 1} \Rightarrow y - 1 = \frac{2}{x - 1} \Rightarrow x - 1 = \frac{2}{y - 1} \Rightarrow x = \frac{2}{y - 1} + 1$

38) أبين أن $\frac{d x}{d y} = \frac{1}{\frac{d y}{d x}}$

$S o l u t i o n : y = 1 + \frac{2}{x - 1} \Rightarrow \frac{d y}{d x} = - \frac{2}{{(x - 1)}^{2}} x = 1 + \frac{2}{y - 1} \Rightarrow \frac{d x}{d y} = - \frac{2}{{(y - 1)}^{2}} b u t {(y - 1)}^{2} = \frac{4}{{(x - 1)}^{2}} \Rightarrow \frac{d x}{d y} = - \frac{2}{\frac{4}{{(x - 1)}^{2}}} = - \frac{{(x - 1)}^{2}}{2} = \frac{1}{\frac{d y}{d x}} \Rightarrow \frac{d x}{d y} = \frac{1}{\frac{d y}{d x}}$

تبرير: إذا كان: $f (x) = \frac{l n x}{x^{2}}$ فأجيب عن السؤالين الآتيين تباعًا:

39) أثبت أن $f'' (x) = \frac{6 l n x - 5}{x^{4}}$ مُبرّرًا إجابتي.

$S o l u t i o n : f^{'} (x) = \frac{\frac{d}{d x} (l n x) x^{2} - l n x \frac{d}{d x} (x^{2})}{x^{4}} = \frac{(\frac{1}{x}) x^{2} - l n x (2 x)}{x^{4}} = \frac{x - 2 x l n x}{x^{4}} = \frac{1 - 2 l n x}{x^{3}} f^{''} (x) = \frac{\frac{d}{d x} (1 - 2 l n x) x^{3} - (1 - 2 l n x) \frac{d}{d x} (x^{3})}{x^{6}} = \frac{(\frac{- 2}{x}) x^{3} - (1 - 2 l n x) (3 x^{2})}{x^{6}} = \frac{- 2 x^{2} - 3 x^{2} + 6 x^{2} l n x}{x^{6}} = \frac{6 x^{2} l n x - 5 x^{2}}{x^{6}} f^{''} (x) = \frac{6 l n x - 5}{x^{4}}$

40) أجد قيمة المقدار: $x^{4} f^{''} (x) + 4 x^{3} f^{'} (x) + 2 x^{2} f (x) + 1$

$S o l u t i o n : x^{4} f^{''} (x) + 4 x^{3} f^{'} (x) + 2 x^{2} f (x) + 1 = = x^{4} (\frac{6 l n x - 5}{x^{4}}) + 4 x^{3} (\frac{1 - 2 l n x}{x^{3}}) + 2 x^{2} (\frac{l n x}{x^{2}}) + 1 = 6 l n x - 5 + 4 (1 - 2 l n x) + 2 l n x + 1 = 6 l n x - 5 + 4 - 8 l n x + 2 l n x + 1 = 8 l n x - 8 l n x - 5 + 5 = 0 z e r o$

رياضيات فصل أول

التوجيهي علمي

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS