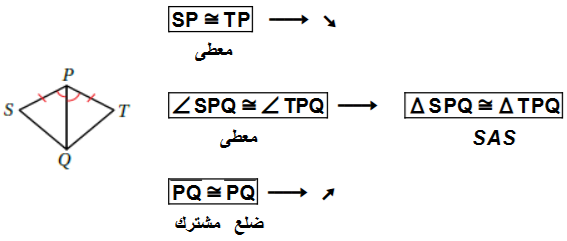
أتحققُ من فهمي 1 : أثبتُ أنَّ المثلثَينِ المبيّنَينِ في الشكلِ المجاورِ متطابقانِ باستعمالِ البرهانِ السهميِّ.
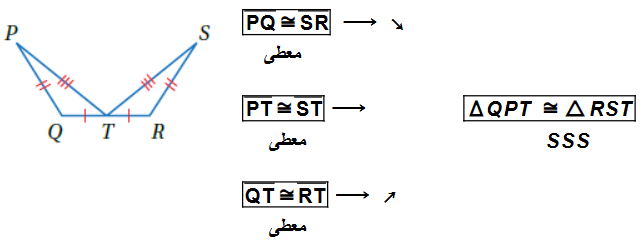
أتحققُ من فهمي 2 : أثبتُ أنَّ المثلثَينِ المبيّنَينِ في الشكلِ المجاورِ متطابقانِ، باستعمالِ البرهانِ ذي العمودَينِ.
| العبارات | المبررات |
| معطى | |
| معطى | |
| تقابل بالرأس | |
| SAS |
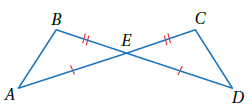
أتحققُ من فهمي 3 : بساطٌ: يبيّنُ الشكلُ المجاورُ بساطًا تقليديًّا يستعملُ الحائكُ في تصميمِهِ انسحابًا لمثلثٍ متطابقِ الضلعَينِ. أثبتُ أنّ , المبيّنَينِ في الشكلِ متطابقانِ باستعمالِ البرهانِ ذي العمودَينِ.
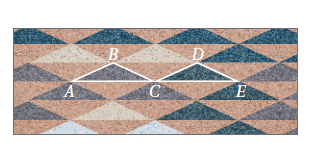
بما أن المثلثين متطابقا الضلعين إذاً زوايا القاعدتين متطابقة في المثلثين وبالتالي الزاوية الثالثة من كل مثلث متطابقة مع الأخرى وعليه :
| العبارات | المبررات |
| معطى | |
| معطى | |
| نتيجة | |
| SAS |
حل آخر :
بما أن المثلث الثاني يمثل انسحاباً للمثلث الأول ، إذاً فهو متطابق معه تماماً وبالتالي فالأضلاع المتناظرة متطابقة وعليه :
| العبارات | المبررات |
| معطى | |
| معطى | |
| معطى | |
| SSS |
أتحققُ من فهمي 4 : في الشكلِ المجاورِ، إذا علمْتُ أنَّ فأثبت أن باستعمالِ البرهانِ السهميِّ.
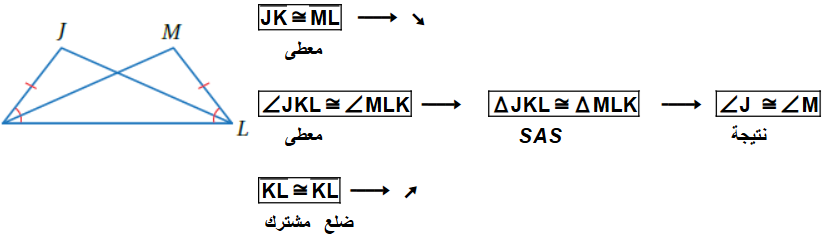
أتحققُ من فهمي 5 : أستعملُ المعلوماتِ المعطاةَ في الشكلِ المجاورِ في كتابةِ برهانٍ ذي عمودَينِ ، لأثبتَ أن
الحل : من الواضح أن المثلثين قائمي الزاوية وبالتالي نحتاج فقط إلى وتر وضلع في المثلث الأول متطابق مع وتر وضلع في المثلث الثاني .
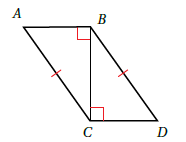
| العبارات | المبررات |
| معطى(وتر) | |
| زاوية قائمة | |
| ضلع مشترك | |
| HL |
أتدرب وأحل مسائل
أبيّنُ أنَّ كلَّ زوجٍ مِنَ المثلثاتِ الآتيةِ متطابقٌ أَمْ لا، مبررًا إجابتي:
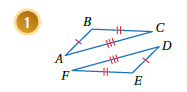
المثلثين متطابقين بثلاثة أضلاع SSS حيث :
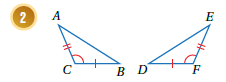
المثلثين متطابقين بضلعين وزاوية محصورة حيث :
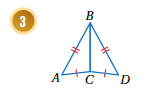
المثلثين متطابقين بثلاثة أضلاع SSS حيث :
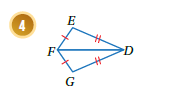
المثلثين متطابقين بثلاثة أضلاع SSS حيث :
5) أستعمل المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ ذي عمودَينِ ؛ لأثبتَ أنَّ .
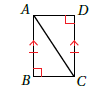
| العبارات | المبررات |
| زاوية قائمة | |
| معطى | |
| وتر (ضلع مشترك) | |
6) أستعمل المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ ذي عمودَينِ ؛ لأثبتَ أنَّ .
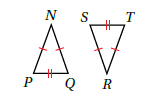
| العبارات | المبررات |
| معطى | |
| معطى | |
| معطى | |
| SSS |
7) استعمل المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ سهمي ؛ لأثبتَ أنَّ .
8) استعمل المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ سهمي ؛ لأثبتَ أنَّ
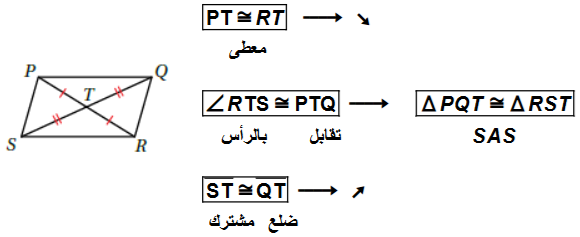
9) أستعمل المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ ذي عمودَينِ ؛ لأثبتَ أنَّ .
| العبارات | المبررات |
| معطى | |
| معطى | |
| ضلع مشترك | |
| SSS | |
| نتيجة |
توضيح للنتيجة : بما أن المثلثين متطابقين وبالتالي أضلاعهما متطابقة وزواياهما متطابقة .
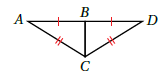
10) استعمل المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ سهمي ؛ لأثبتَ أنَّ .
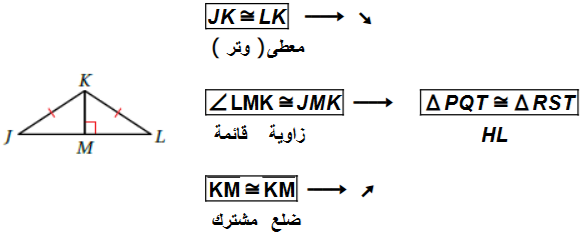
مصباحٌ: يبيّنُ الشكلُ المجاورُ الضوءَ الناشئَ عَنْ مصباحَينِ يبعدانِ المسافةَ نفسَها عَنْ أرضيةِ مسرحٍ:
11) أثبت أنّ :
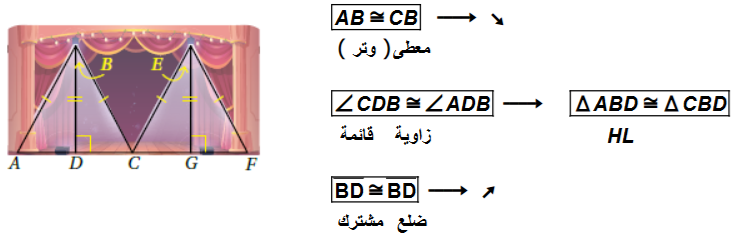
12) هَلِ المثلثاتُ الأربعةُ الموضَّحةُ في الشكلِ متطابقةٌ؟ أبرّرُ إجابتي.
نعم جميع المثلثات متطابقة لأن امصباحان يبعدان المسافة نفسها عن أرض المسرح ـ توضيح :
في الشكلِ المجاورِ المثلثانِ
13) أكتبُ برهانًا ذا عمودَينِ؛ لأثبتَ أنَّ .
| العبارات | المبررات |
| العبارات | المبررات |
| معطى | |
| معطى | |
| تقابل بالرأس | |
| SAS |
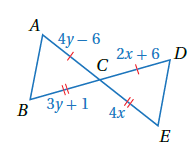
14) أجدُ قيمةَ كلٍّ مِنْ X و y .
بما أن : إذن ومنه
وبما أن : إذن
وبالتعويض في أي معادلة :
15) اتّصالاتٌ: برجُ اتّصالاتٍ عموديٌّ على الأرضِ، يتصلُ رأسُهُ بكلّ مِنَ النقاطِ D و B و C عَنْ طريقِ كابلاتٍ لَها الطولُ نفسُهُ كما في الشكلِ المجاورِ. أثبتُ أنَّ و و متطابقة .
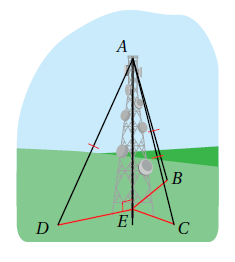
بما أن برج الاتصالات عمودي على الأرض ، فإنه يصنع زاوية قائمة وبالتالي سيتشكل عندنا ثلاثة مثلثات قائمة الزاوية ومنها سنحتاج إلى وتَر وضلع متطابقين مع باقي المثلثات فقط لإثبات أن المثلثات متطابقة .
| العبارات | المبررات |
| زاوية قائمة | |
| معطى | |
| وتر (ضلع مشترك) | |
16) تحدٍّ : أثبتُ أنَّ مستعملاً حالتي SSS و SAS من دون استعمال المنقلة لقياس الزوايا.
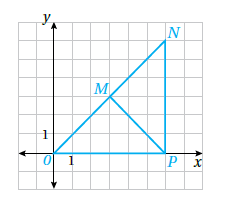
1)يمكن معرفة أطوال الأضلاع عن طريق العد ، ولذلك من الواضح عن طريق عد المربعات أن :
| العبارات | المبررات |
| معطى | |
| معطى | |
| ضلع مشترك | |
| SSS |
2) نلاحظ أن الضلع المشترك بين المثلثين والخارج من النقطة P يقطع المربعات في المستوى البياني من المنتصف : وبالتالي يصنع زاويتين متساويتين مقدار كل منهما 45 درجة .
| العبارات | المبررات |
| معطى | |
| ضلع مشترك | |
| نتيجة (حسب الملاحظة) | |
| SAS |
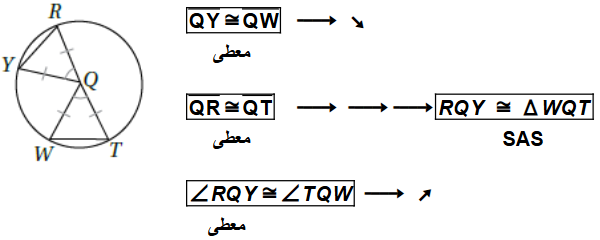
17) تبريرٌ: في الشكلِ المجاورِ، إذا علمْتُ أنَّ و مركزُ الدائرةِ، فأكتبُ برهانًا ذا عمودَينِ؛ لإثباتِ أنَّ ، مبرراً إجابتي .
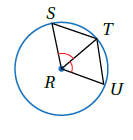
| العبارات | المبررات |
| نصف قطر | |
| ضلع مشترك | |
| معطى | |
| SAS |
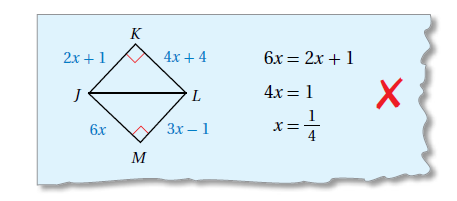
18) اكتشف : أحددُ الخطأَ في إيجادِ قيمةِ x في الحلِّ الآتي الّتي تجعلُ المثلثَينِ متطابقَينِ، وأصحّحُهُ .
الخطأ هو أن لأن .
19) تحدٍّ: أستعملُ المعلوماتِ المعطاةَ في الشكلِ الآتي : لأثبتَ أنَّ .
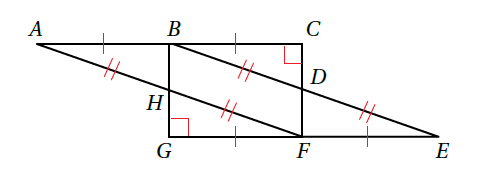
من الواضح أن الشكل BCFG يمثل مستطيلاً لأن زواياه قوائم وفيه ضلعان متقابلان متطابقان .
| العبارات | المبررات |
| معطى | |
| معطى | |
| ضلعين متقابلين في مستطيل | |
| SSS |
20) أكتبُُ كيفَ أتحققُ مِنْ تطابقِ مثلثَينِ بثلاثةِ أضلاع، أَوْ ضلعَينِ وزاويةٍ محصورةٍ بينَهُما.
يمكن التحقق من تطابق المثلثين عن طريق مقارنة الأضلاع المتناظرة في المثلثين مع بعضها .
ومقارنة الزوايا المتناظرة في المثلثين مع بعضها.
أسئلة كتاب التمارين :
أحددُ المسلمةَ الّتي تساعدُني على إثباتِ تطابقِ كلِّ زوجٍ مِنَ المثلثاتِ الآتيةِ:
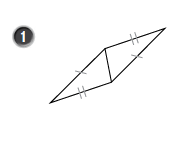
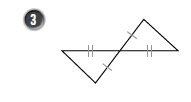
1) SSS : من المعطيات واضح أن هناك ضلعان متطابقان ، ونلاحظ أن هناك ضلع مشترك .
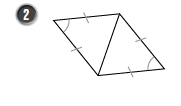
2) SAS : من المعطيات واضح أن كل مثلث يحوي ضلعان متطابقان وزاوية محصورة متطابقة مع المثلث الآخر .
3) SAS : من المعطيات واضح أن كل مثلث يحوي ضلعان متطابقان وزاوية محصورة متطابقة مع المثلث الآخر .
ملاحظة : قمنا بمعرفة أن الزاويتين متطابقتين عن طريق التقابل بالرأس .
4) أستعملُ المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ ذي عمودَينِ؛ لأثبتَ أنَّ .
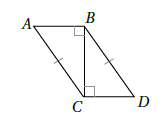
| العبارات | المبررات |
| زاوية قائمة | |
| معطى(وتر) | |
| ضلع مشترك | |
5) أستعملُ المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ ذي عمودَينِ؛ لأثبتَ أنَّ 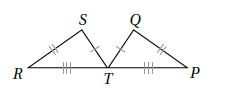 .
.
| العبارات | المبررات |
| معطى | |
| معطى | |
| معطى | |
| SSS |
6) أستعملُ المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ سهمي ؛ لأثبتَ أنَّ .
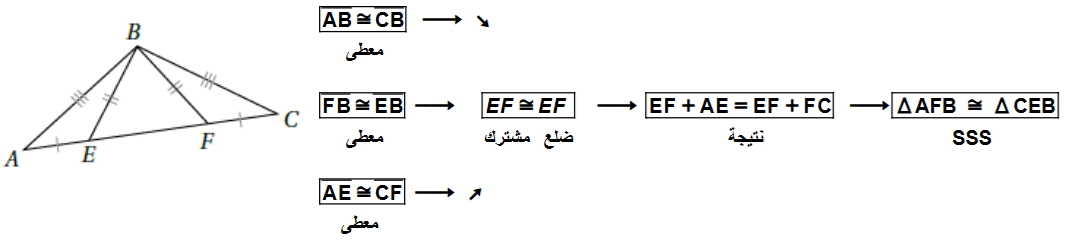
7 ) أستعملُ المعلوماتِ المعطاةَ في الشكلِ الآتي لكتابةِ برهانٍ سهميٍّ؛ لأثبتَ أنَّ : .
إذا كان فأجدُ كلًّ ممّا يأتي :
ملاحظة مساعدة في الحل : دون الحاجة للرسم يمكننا مقارنة الأحرف المتناظرة حسب التسمية فمثلاً في المثلثين المعطيين :
(مجموع زوايا المثلث 180 )
12) تبدو الطائراتُ في العرضِ الجوّيِّ كأنَّها مثلثَينِ بينَهُما ضلعٌ مشتركٌ. أكتبُ برهانًا ذا عمودَينِ أثبتُ فيهِ أنَّ حيث T نقطة منتصف و
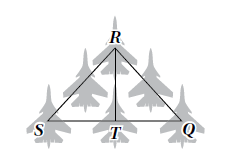
| العبارات | المبررات |
| لأن T نقطة المنتصف | |
| ضلع مشترك | |
| معطى | |
| SSS |