حلول أسئلة كتاب الطالب وكتاب التمارين
حلول أسئلة أتحقق من فهمي
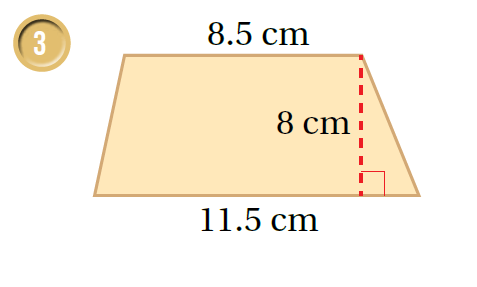
أتحقق من فهمي صفحة 102
أجدُ مساحة شبه المُنحرف في كُلّ ممّا يأتي:
 |
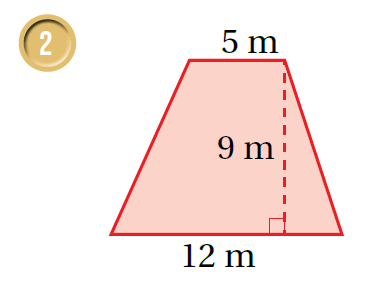 |
| صيغةُ مساحة شبه المُنحرف | صيغةُ مساحة شبه المُنحرف |
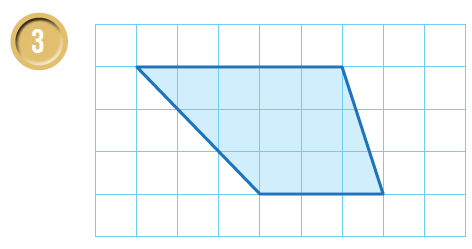
أتحقق من فهمي صفحة 103
أجدُ مساحة شبه المُنحرف في كُلّ شبكة ممّا يأتي:
 |
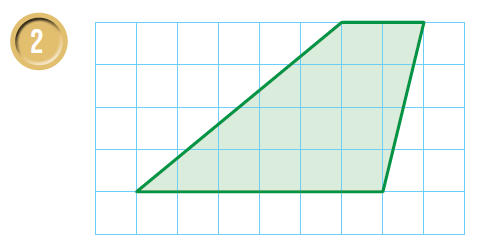 |
| هنا نعدّ الوحدات الأفُقيّة والرّأسيّة لنجد طول كُلّ من القاعدتين b2 ، b1 والارتفاع h | |
أتحقق من فهمي صفحة 104
حديقةٌ على شكل شبه مُنحرفٍ، طولُ كُلٍّ من قاعدتيه 30 m و 40 m والمسافةُ العموديّةُ بين القاعدتين 35 m ، أجدُ مساحة هذه الحديقة.
الجواب
أتحقق من فهمي صفحة 105
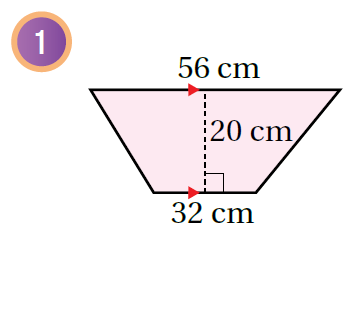
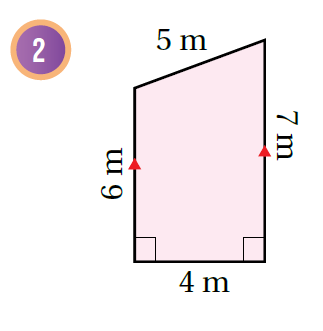
أجدُ مساحة المنطقة المُظلّلة في كُلّ شكل ممّا يأتي:
 |
 |
| مساحة شبه المُنحرف | مساحة شبه المُنحرف الأعلى |
| مساحة المثلث | مساحة شبه المُنحرف الأسفل |
| مساحة المنطقة المظللة | مساحة المنطقة المظللة |
حلول أسئلة أتدرب وأحل المسائل
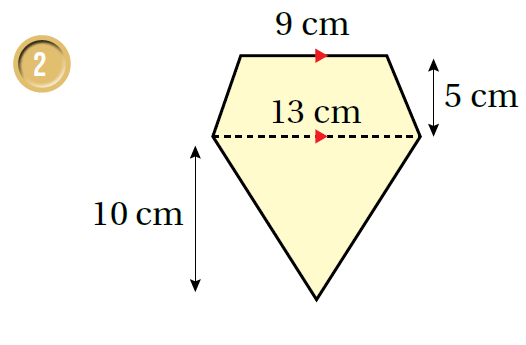
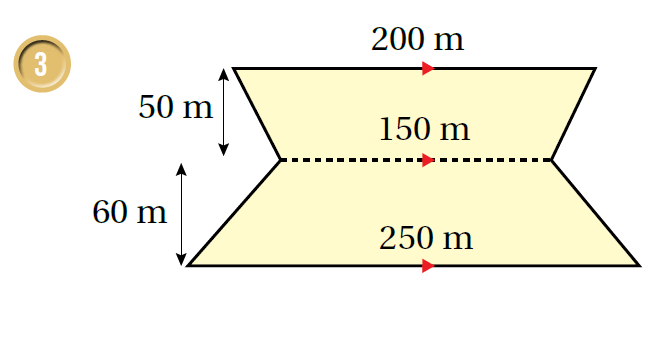
أجدُ مساحة شبه المُنحرف في كُلٍّ ممّا يأتي:
 |
 |
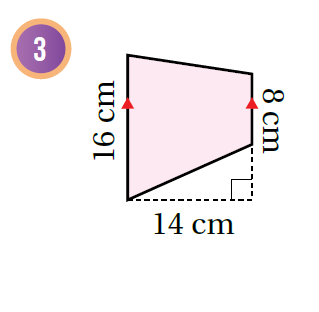 |
أجدُ مساحة شبه المُنحرف في كُلّ شبكةٍ ممّا يأتي:
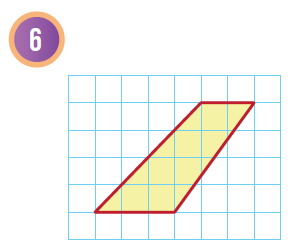 |
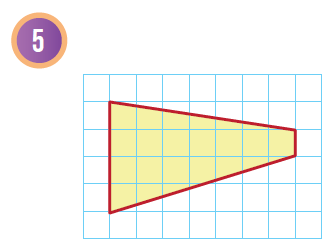 |
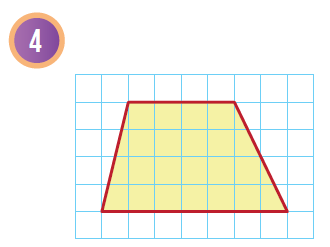 |
| هنا نعدّ الوحدات الأفُقيّة والرّأسيّة لنجد طول كُلّ من القاعدتين b2 ، b1 والارتفاع h | ||
أجدُ مساحة المنطقة المُظلّلة في كُلٍّ ممّا يأتي:
 |
 |
|
9) مكتبٌ: إذا صنع عمرانُ مكتبًا على شكل حرف L بحسب المقاسات المُبيّنة في الشّكل المُجاور، فأجدُ مساحة سطح المكتب. الجواب نلاحظ أن الشكل مقسم إلى شبهي منحرف وهما (A) و (B). مساحة سطح المكتب = A + B
|
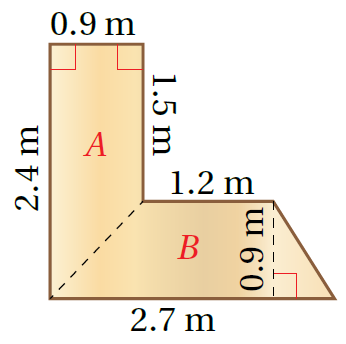 |
حلول أسئلة مهارات التفكير العُليا
10) أكتشفُ الخطأ: أوجد سالمٌ مساحة الشّكل المُركّب أدناهُ، وكان حلُّهُ كما هُو مُبيّنُ، أُبيّنُ الخطأ الّذي وقع فيه سالمٌ، وأُصحّحُهُ.
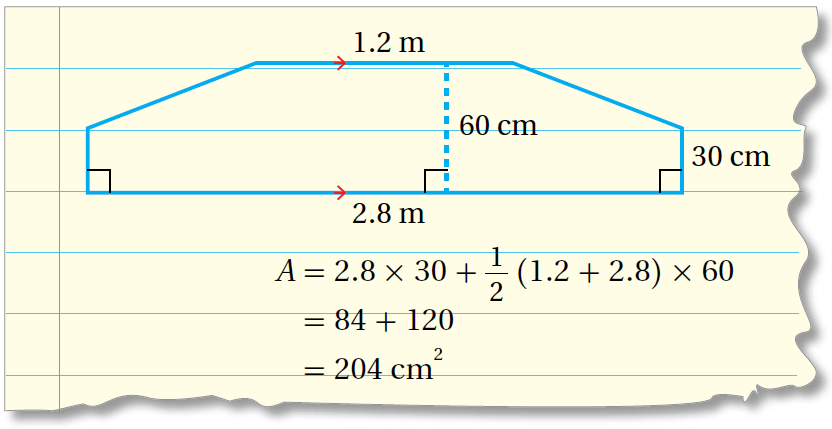
الجواب
الخطأ: أخطأ سالم في تحديد ارتفاع شبه المنحرف فحسبه والصحيح أن ارتفاعه كما أنه لم يقم بتوحيد الوحدات في السؤال.
الصواب: لإيجاد مساحة الشكل؛ نقوم أولا بتوحيد الوحدات، فمثلا نحول وحدة المتر إلى سنتيمتر.
فتكون المساحة:
11) تحدٍّ: يظهرُ في الشّكل المُجاور مُتوازي أضلاعٍ وشبهُ مُنحرفٍ مُتساويان في المساحة، أجدُ ارتفاع شبه المُنحرف h لقرب عددٍ صحيحٍ.
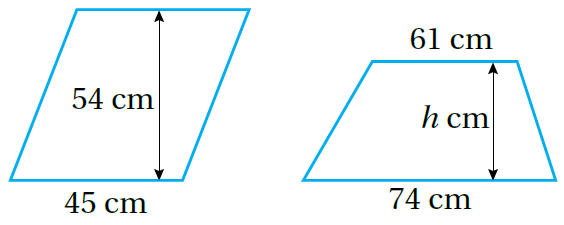
الجواب
- مساحة متوازي الأضلاع = مساحة شبه المنحرف
| مساحة متوازي الأضلاع | |
| مساحة شبه المنحرف | |
12) أكتب كيف أجدُ مساحة شبه المُنحرف؟
الجواب
لإيجاد مساحة شبه المنحرف أجد طول قاعدتي شبه المنحرف وهما الضلعان المتوازيان فيه، ثم أحدد ارتفاعه وهو المسافة بين القاعدتين ثم أجد ناتج ضرب نصف مجموع القاعدتين في الارتفاع.
حلول أسئلة كتاب التمارين
أجدُ مساحة شبه المُنحرف في كُلّ شكل ممّا يأتي:
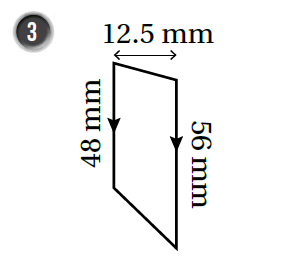 |
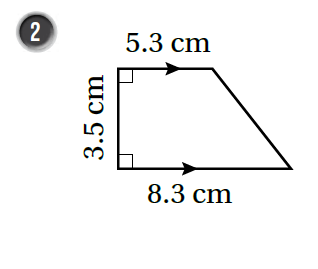 |
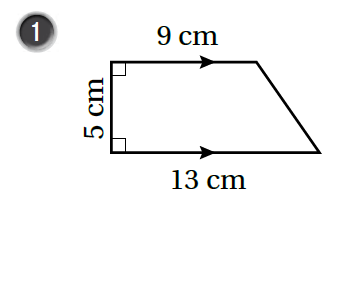 |
أجدُ مساحة شبه المُنحرف في كُلّ شبكة ممّا يأتي:
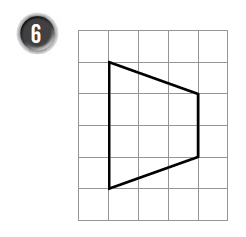 |
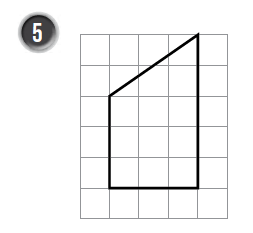 |
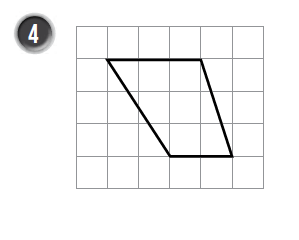 |
أجدُ مساحة المنطقة المُظلّلة في كُلّ ممّا يأتي:
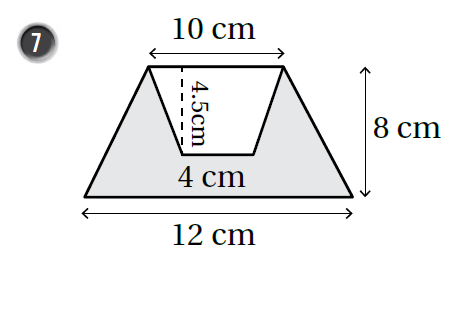 |
 |
| مساحة شبه المنحرف الداخلي الغير مظلل | مساحة شبه المنحرف الأيسر |
| مساحة شبه المنحرف الكبير | مساحة شبه المنحرف الأسفل |
| مساحة المنطقة المظللة | مساحة المنطقة المظللة |
9) يُبيّنُ الشّكلُ المُجاورُ مُثلّثًا وشبه مُنحرف لهُما المساحةُ نفسُها. أجدُ قيمة x في المُثلّث.
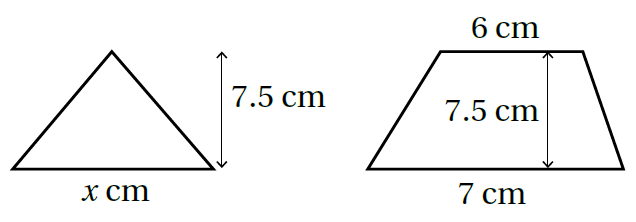
الجواب
| مساحة شبه المنحرف |
| مساحة المثلث |
|
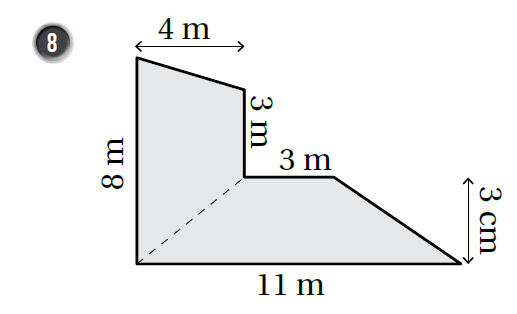
10) زراعةٌ: تُريدُ سوزانُ زراعة قطعة الأرض المُبيّنة في الشّكل المُجاور. إذا لزم لتسميد كُلّ من قطعة الأرض من السّماد، فكم كيلوغرامًا من السّماد تحتاجُ إليها سوزانُ لتسميد قطعة الأرض؟ الجواب
|
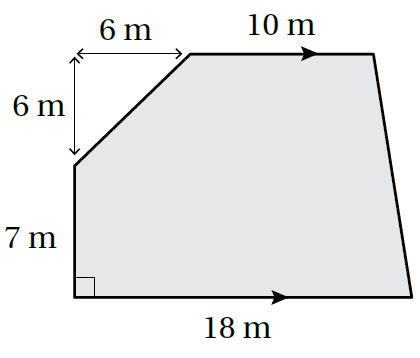 |