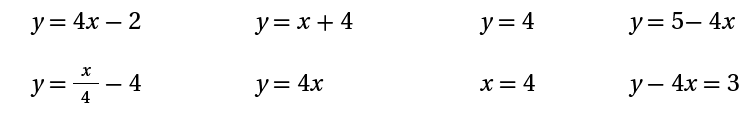رياضيات فصل أول

أتحقق من فهمي(1)

أجدُ ميلَ المستقيمِ المارِّ بكلِّ نقطتينِ ممّا يأتي:

1) $(-1, 2), (3, 5)$

$(x_1, y_1)\to (-1, 2), (x_2, y_2)\to (3, 5)$

 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{5-2}{3-(-1)}=\frac{3}{4}$

 

2) $( -1, -2), ( -4, 1)$

$(x_1, y_1)\to (-1, -2), (x_2, y_2)\to (-4, 1)$

 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{1-(-2)}{-4-(-1)}=\frac{3}{-3}=-1$

 

3) $(1, 2), ( -3, 2)$ 

$(x_1, y_1)\to (1, 2), (x_2, y_2)\to (-3, 2)$

 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{2-2}{-3-1}=\frac{0}{-4}=0$

 

4) $(1, 5) ,( 1, -4)$

$(x_1, y_1)\to (1, 5), (x_2, y_2)\to (1, -4)$ 

 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{-4-5}{1-1}=\frac{-9}{0}$    غير معرف

 

أتحقق من فهمي(2)

أجدُ قيمةَ k التي تجعلُ ميلَ المستقيمِ المارِّ بالنقطتينِ  (1 , 3) و (k, 2) يساوي $-\frac{1}{6}$

$(x_1, y_1)\to (3, 1), (x_2, y_2)\to (k, 2)$

$m=\frac{y_2-y_1}{x_2-x_1}$

$-\frac{1}{6}=\frac{2-1}{k-3}$

$k-3=-6\Rightarrow k=-3$

 

أتحقق من فهمي(3)

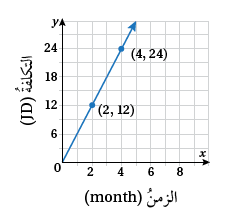
يبيّنُ التمثيلُ البيانيُّ المجاورُ متوسطَ تكلفةِ تشغيلِ ثلاجةٍ (بالدينارِ) أشهرًا عدةً. 

1) أجدُ تكلفةَ تشغيلِ الثلاجةِ مدةَ 3 أشهرٍ. 

التكلفة 18 ديناراً

 

2) أجدُ معدّلَ تغيّرِ تكلفةِ تشغيلِ الثلاجةِ بالنسبةِ إلى الزمنِ، ثمَّ أوضّحُ ماذا يمثّلُ. 

$(x_1, y_1)\to (2, 12), (x_2, y_2)\to (4, 24)$

 

                                                           $m=\frac{y_2-y_1}{x_2-x_1}=\frac{24-12}{4-2}=\frac{12}{2}=6$

ميل المستقيم هو 6، وهو يمثل معدل التغير في التكلفة بالدينار لكل شهر، حيث أن التكلفة تزداد بمقدار 6 دنانير شهرياً

 

أتدرب وأحل المسائل

أجدُ ميلَ المستقيمِ المارِّ بكلِّ نقطتينِ ممّا يأتي:

1) $(3, 3), (5, 7)$

$(x_1, y_1)\to (3, 3), (x_2, y_2)\to (5, 7)$

 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{7-3}{5-3}=\frac{4}{2}=2$

 

2) $(6,1), (4,3)$

$(x_1, y_1)\to (6, 1), (x_2, y_2)\to (4, 3)$

 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{3-1}{4-6}=\frac{-2}{2}=-1$

 

3) $(-2, -6), (-2, 6)$

$(x_1, y_1)\to (-2, -6), (x_2, y_2)\to (-2, 6)$

 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{6-(-6)}{-2-(-2)}=\frac{12}{0}$ غير معرف

 

4) $(5, -7), (0, -7)$

$(x_1, y_1)\to (5, -7), (x_2, y_2)\to (0, -7)$

 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{-7-(-7)}{0-5}=\frac{0}{-5}=0$

 

5) $( -1, 0), ( 0, -5)$

$(x_1, y_1)\to (-1, 0), (x_2, y_2)\to (0, -5)$

 

$m=\frac{y_2-y_1}{x_2-x_1}= \frac{-5-0}{0-(-1)}=\frac{-5}{1}=-5$

 

6) $(4, 1), (12, 8)$

$(x_1, y_1)\to (4, 1), (x_2, y_2)\to (12, 8)$

 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{8-1}{12-4}= \frac{7}{8}$

 

أجدُ قيمةَ s التي تجعلُ مَيلَ المستقيمِ (m) المارِّ بكلِّ نقطتينِ ممّا يأتي على نحوِ ما هو مُعْطًى:

7) $(6, -2), (s, -6) , m = 4$

$(x_1, y_1)\to (6, -2), (x_2, y_2)\to (s, -6)$

$m=\frac{y_2-y_1}{x_2-x_1}$

 

$4=\frac{-6-(-2)}{s-6}$

 

$4s-24=-4$

$4s=20\Rightarrow s=5$

 

8) $(9, s), (6, 3), m =-\frac{1}{3}$

$(x_1, y_1)\to (6, 3), (x_2, y_2)\to (9, s)$

 

$m=\frac{y_2-y_1}{x_2-x_1}$

 

$-\frac{1}{3}=\frac{s-3}{9-6}$

 

$3s-9=-3$

$3s=6\Rightarrow s=2$

 

 

أحدّدُ ما إذا كانَ ميلُ كلِّ مستقيمٍ ممّا يأتي سالبًا أم موجبًا أم صفرًا أم غيرَ معرَّفٍ ، ثمَّ أجِدُه:

            
     

                                     

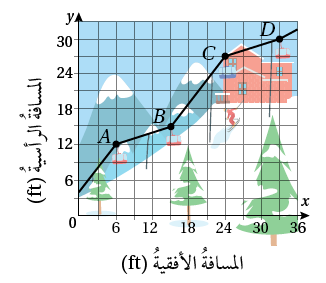
تزلّجٌ: يبيّنُ التمثيلُ البيانيُّ المجاورُ  المنظرَ الجانبيَّ لمِصْعدِ تزلُّجٍ.

 

12) أجدُ مَيلَ كلٍّ منْ: $\overline{AB} , \overline{BC} ,\overline{ CD}$

$\overline{AB}:(x_1, y_1)\to (6, 12), (x_2, y_2)\to (15, 15)$

 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{15-12}{15-6}=\frac{3}{9}=\frac{1}{3}$ 

 

 

$\overline{BC}:(x_1, y_1)\to (15, 15), (x_2, y_2)\to (24, 27)$

 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{27-15}{24-15}=\frac{12}{9}=\frac{4}{3}$

 

$\overline{CD}:(x_1, y_1)\to (24, 27), (x_2, y_2)\to (33, 30)$

 

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{30-27}{33-24}=\frac{3}{9}=\frac{1}{3}$

 

13) أيُّ جزءٍ منْ مِصْعدِ التزلُّجِ يُعدُّ الأشدَّ انحدارًا؟ أُبرّرُ إجابتِي.

$\left(BC\right)$ هو الأشد انحداراً لأن ميله هو الأكبر

14) منحَدَراتٌ: تنصُّ قوانينُ البناءِ المتعلِّقةُ بمنحَدراتِ وصولِ الأشخاصِ ذوي الإعاقةِ الحركيّةِ إلى الأبنيةِ على أنَّ كلَّ ارتفاعٍ رأسيٍّ بمقدارِ $0.4 m$ يتطلّبُ مسارًا أفقيًّا طولُه $4.8 m$ . أجدُ مَيلَ هذا المُنحَدَرِ.

$m=\frac{∆y}{∆x}= \frac{0.4}{4.8}= \frac{1}{12}$

 

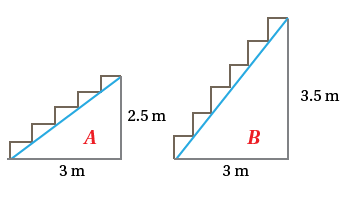
15) درجٌ: يبيّنُ الشكلُ المجاورُ دَرجَينِ مُصَمَّمينِ للدخولِ إلى أحدِ المباني. فأيُّ الدرجينِ أختارُ صعودَهُ للدخولِ
إلى المبنى؟ أبرّرُ إجابتِي.

اختار المدرج $A$ لأن انحداره أقل عدد درجاته أقل

 

 

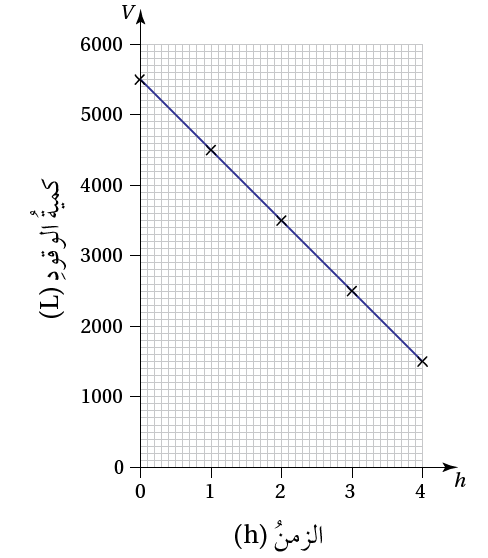
طائرةٌ: يبيّنُ التمثيلُ البيانيُّ المجاورُ كميّةَ الوقودِ V باللتراتِ في خزّانِ طائرةٍ بعدَ h ساعة.

 

16) ما كميّةُ الوقودِ في خزانِ الطائرةِ عندَ انطلاقِها؟

5500 لتر

 

17) ما كميّةُ الوقودِ في الخزانِ بعدَ مرورِ 3.5 h ؟

2000 لتر 

 

18) أجدُ معدّلَ تغيّرِ كميّةِ الوقودِ في الخزانِ بالنسبةِ إلى الزمنِ، ثمَّ أُبيّنُ ماذا يمثّلُ

$(x_1, y_1)\to (0, 5500), (x_2, y_2)\to (3.5, 2000)$

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{2000-5500}{3.5-0}=\frac{-3500}{3.5}=-1000$

 

ميل المستقيم $-1000$، وهو يمثل معدل استهلاك الوقود بالنسبة لكل ساعة، حيث أن خزان الوقود ينقص بمقدار 1000 لتر كل ساعة

19) أكتشفُ الخطأَ: أوجَدَ مهندٌ مَيلَ المستقيمِ المارِّ بالنقطتينِ $(5, 4), (0, 2)$، وكانَ حَلُّه على النحوِ الآتي:

 ✘ $m=\frac{2-4}{5-0}=\frac{-2}{5}$

أُبيّنُ الخطأَ الذي وقعَ فيهِ مهندٌ وأُصحِّحُه.

لم يلتزم مهند بالترتيب والحل الصحيح هو:  $m=\frac{2-4}{0-5}=\frac{-2}{-5}=\frac{2}{5}$

20) تبريرٌ: هل تقعُ النقاطُ (4, A(1, 3), B(4, 2), C(-2 على المستقيمِ نفسِه؟ أبرّرُ إجابتي.

$\overline{AB}:(x_1, y_1)\to (1, 3), (x_2, y_2)\to (4, 2)$

           $m=\frac{y_2-y_1}{x_2-x_1}= \frac{2-3}{4-1}= \frac{-1}{3}$

 

$\overline{BC}:(x_1, y_1)\to (4, 2), (x_2, y_2)\to (-2, 4)$

   $m=\frac{y_2-y_1}{x_2-x_1}=\frac{4-2}{-2-4}=\frac{2}{-6}=\frac{-1}{3}$

  تقع النقاط على استقامة واحدة لأن الميل متساوي
 

21) مسألةٌ مفتوحةٌ: أجدُ نقطتينِ تقعانِ على مستقيمٍ ميلُه $-9$

النقطتان: $(1, 10), (2, 1)$

22) أكتب: كيفَ أجدُ مَيلَ مستقيمِ مارٍّ بنقطتينِ؟

لإيجادِ ميلِ المستقيمِ غيرِ الرأسيِّ في المستوى الإحداثيِّ يُمكِنُنا إيجادُ نسبةِ التغَيُّرِ في الإحداثيِّ Y (التغَيُّرِ الرأسيِّ) إلى التغَيُّرِ في الإحداثيِّ X (التغَيُّرِ الأفقيِّ) بينَ أيِّ نقطتينِ على المستقيمِ.

 

كتاب التمارين

1) أجدُ ميلَ كلِّ مستقيمٍ ممّا يأتي: 

$m=\frac{∆y}{∆x}$

$a\Rightarrow m=\frac{4}{1}=4, b\Rightarrow m=\frac{-4}{4}=-1$

 

$c\Rightarrow \frac{-6}{3}=-2, d\Rightarrow m=\frac{4}{1}=4$

 

$e\Rightarrow m=\frac{4}{8}=\frac{1}{2} , f\Rightarrow m=\frac{3}{4}=0.75$

 

$g\Rightarrow m=\frac{-3}{6}=\frac{-1}{2} ,h\Rightarrow m=\frac{3}{2}=1.5$

 

 

أجدُ ميلَ كلِّ ضلعٍ مِنْ أضلاعِ الأشكالِ الآتيةِ:

$m=\frac{∆y}{∆x}$

$\overline{PQ}\Rightarrow m=\frac{1}{2}, \overline{QR}\Rightarrow m=0$

$\overline{RS}\Rightarrow m=\frac{5}{1}=5 , \overline{SP}\Rightarrow m=\frac{-4}{4}=-1$

 

 

 

 

   

 

 

 

 

 $m=\frac{∆y}{∆x}$

$\overline{JK}\Rightarrow m=\frac{-2}{4}=\frac{-1}{2}$

$\overline{KL}\Rightarrow m=\frac{4}{2}=2$

$\overline{LM}\Rightarrow m=\frac{-2}{4}=\frac{-1}{2}$

$\overline{MJ}\Rightarrow m=\frac{4}{2}=2$

 

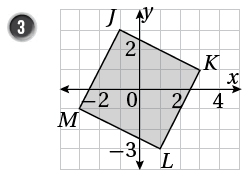
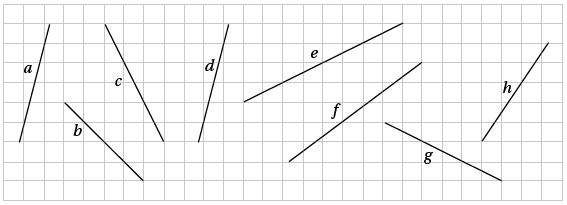
4) أختارُ الميلَ المناسبَ لكلِّ مستقيمٍ ممّا يأتي مِنَ الصندوقِ أدناهُ:

$a) 3 b) -2 c) -0.5 d) 1$                           

 

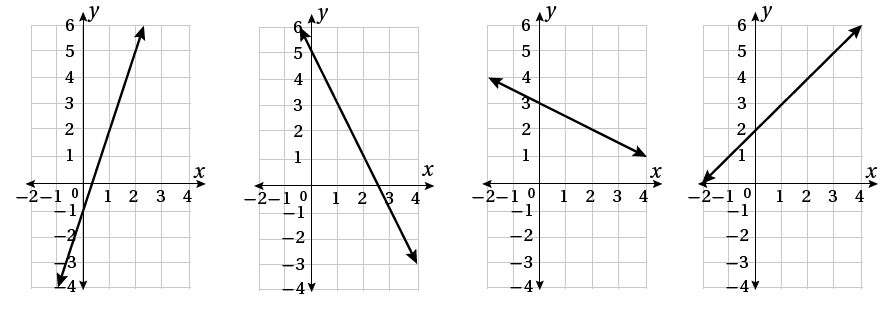
5) أضعُ دائرةً حولَ معادلةِ المستقيمِ الّذي ميلُهُ 4:

الإجابة:  $y=4x-2 , y=4x , y-4x=3$

 

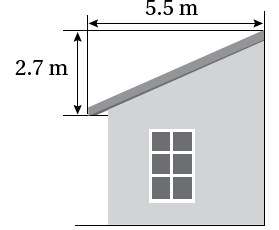
6) أجدُ ميلَ سطحِ المنزلِ المجاورِ. 

 $m=\frac{∆y}{∆x}=\frac{2.7}{5.5}=\frac{27}{55}$

 

 

 

 

 

 

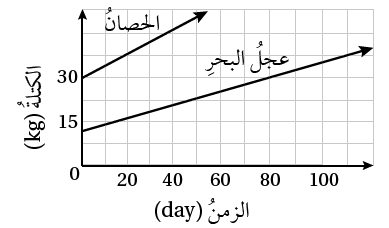
7) يبينُ التمثيلُ المجاورُ متوسطَ معدلِ نموِّ كلٍّ مِنْ عِجْلِ البحرِ والحصانِ، أيُّ الحيوانَينِ لَهُ أسرعُ معدلِ نموٍّ؟ 

معدل نمو الحصان:

$m=\frac{∆y}{∆x}=\frac{37.5-30}{20-0}=\frac{7.5}{20}=\frac{3}{8}$

 

معدل نمو عجل البحر:

$m=\frac{∆y}{∆x}=\frac{30-22.5}{80-50}=\frac{7.5}{30}=\frac{1}{4}$

معدل نمو الحصان أكبر

 

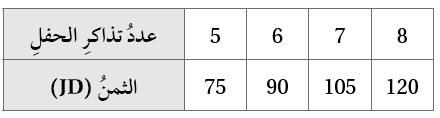
8) أجدُ معدلَ التغيرِ للبياناتِ في الجدولِ الآتي:

عدد التذاكر $x$، الثمن $y$ 

$(x_1, y_1)\to (5, 75), (x_2, y_2)\to (6, 90)$

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{90-75}{6-5}=\frac{15}{1}=15$

 

9) أكتبُ بالصورةِ القياسيةِ معادلةَ مستقيمٍ لَهُ ميلُ المستقيمِ $5x - y = -4$ نفسُهُ.

$5x-y=3$

 

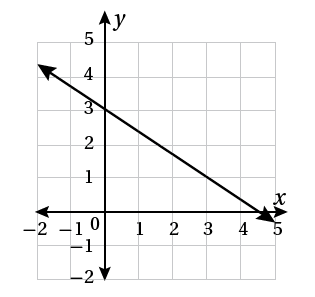
10) أكتشفُ الخطأَ: تقولُ هناءُ إنَّ التمثيلَ البيانيَّ المجاورَ يمثلُ المعادلةَ $3x + 2y = 9$
أكتشفُ الخطأَ الّذي وقعَتْ فيهِ هناءُ، وأصحّحُهُ. 

أخطأت هناء في المعاملات، والحل الصحيح هو:

$2x+3y=9$