رياضيات فصل ثاني

       تدريب   $\left(\mathrm{٦} - \mathrm{١٢}\right)$ صفحة  $\mathbf{٥٦}$ 

      ما معادلة الدائرة التي مركزها نقطة الأصل و تمر بالنقطة     $\left(- \mathrm{١} ، \mathrm{٦} \right)$ ؟

                $$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{{\left(-\mathrm{١} - \mathrm{٠}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left(\mathrm{٦} - \mathrm{٠}\right)}^{\mathbf{٢}}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\sqrt{\mathbf{١}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٣٦}\mathbf{ }}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{٣٧}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }{\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣٧} \end{gathered}$$

 

 

     تدريب   $(\mathrm{٦} -\mathrm{١٣})$ صفحة  $\mathbf{ }\mathbf{ }\mathbf{٥٦}$

    إذا كانت النقطتان   $\mathbf{ }\mathbf{ }\mathit{أ}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٥}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{-}\mathbf{١٢}\mathbf{)}\mathbf{ }\mathbf{،}\mathbf{ }\mathit{ب}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{-}\mathbf{٥}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{١٢}\mathbf{ }\mathbf{)}\mathbf{ }$  نهايتي قطر في دائرة مركزها النقطة م : 

       أ) ما احداثيا مركز الدائرة ؟ 

    ب) ما طول نصف قطر الدائرة ؟ 

     ج) ما معادلة الدائرة ؟ 

$$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{أ}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\left(\frac{\mathrm{٥} + - \mathrm{٥}}{\mathrm{٢}} ، \frac{-\mathrm{١٢} + \mathrm{١٢} }{ \mathrm{٢} }\right)\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ب}\mathbf{)}\mathbf{ }\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{{\left(\mathrm{٥} - \mathrm{٠}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left(-\mathrm{١٢} - \mathrm{٠}\right)}^{\mathbf{٢}}\mathbf{ }}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ج}\mathbf{)}\mathbf{ }\mathbf{ }{\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٦٩} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\left(\mathrm{٠} ، \mathrm{٠} \right)\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\sqrt{\mathbf{٢٥}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١٤٤}}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{١٦٩}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٣}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \end{gathered}$$                  

 

 

       تدريب$\mathbf{ }\mathbf{ }\left(\mathrm{٦} - \mathrm{١٤}\right)$     صفحة  $\mathbf{٥٨}$

           أ) جد معادلة الدائرة التي مركزها النقطة   $\mathbf{ }\mathbf{ }\left(\mathrm{٧} ، \mathrm{٠}\right)$ و تمر بالنقطة  $\left(-\mathrm{١} ، \mathrm{٦}\right)$ ؟

        ب)  جد أحداثيي نقطة المركز و طول قطر الدائرة التي معادلتها   $\mathbf{ }\mathbf{ }{\left(س - \mathrm{٥}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left(ص + \mathrm{٣}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٤٩}$

 

$$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{ }\mathit{أ}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{{\mathbf{(}\mathbf{٧}\mathbf{ }\mathbf{-}\mathbf{-}\mathbf{ }\mathbf{١}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{٠}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٦}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{٦٤}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٣٦}\mathbf{ }}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{١٠٠}}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٠}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \\ {\mathbf{(}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٧}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٠٠}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \end{gathered}$$      ب)    احداثيي المركز =  $\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٥}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{)}\mathbf{ }$      ، طول نصف القطر = $\mathbf{٧}$   ،  طول القطر = $\mathbf{١٤}$

 

    تدريب  $\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٦}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{١٥}\mathbf{ }\mathbf{)}$   صفحة  $\mathbf{٥٩}$  

       جد إحداثي نقطة المركز و طول نصف قطر الدائرة التي معادلتها : 

                 ${\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٢}\mathit{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٦}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{١٥}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{صفرًا}$             

                                    $$\begin{gathered} \mathbf{(}\mathbf{ }\mathbf{ }{\mathbf{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٢}\mathbf{س}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{(}\mathbf{ }{\mathbf{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٦}\mathbf{ }\mathbf{ص}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٥}\mathbf{ } \\ \mathbf{(}\mathbf{ }{\mathbf{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٢}\mathbf{س}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١}\mathbf{)}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{(}\mathbf{ }{\mathbf{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٦}\mathbf{ }\mathbf{ص}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٩}\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٥}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٩}\mathbf{ } \\ \mathbf{ }{\mathbf{(}\mathbf{س}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{ص}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٣}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٢٥}\mathbf{ } \\ \mathbf{احداثي}\mathbf{ }\mathbf{نقطة}\mathbf{ }\mathbf{المركز}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{-}\mathbf{١}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{طول}\mathbf{ }\mathbf{تصف}\mathbf{ }\mathbf{القطر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٥}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{طول}\mathbf{ }\mathbf{القطر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{\times }\mathbf{ }\mathbf{٥}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٠}\mathbf{ } \end{gathered}$$                

 

 

 

      تدريب$\mathbf{ }\mathbf{ }\left(\mathrm{٦} -\mathrm{١٦}\right)$  صفحة  $\mathbf{٥٩}$

      جد إحداثي نقطة المركز و طول قطر الدائرة التي معادلتها : 

             $\mathbf{ }{\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٢}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٦}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{١٥}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{صفرًا}\mathbf{ }$   باستخدام الصورة العامة لمعادلة الدائرة .

 

               $$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{احداثيا}\mathbf{ }\mathbf{نقطة}\mathbf{ }\mathbf{المركز}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\frac{\mathbf{-}\mathbf{ }\mathbf{٢}}{\mathbf{٢}}\mathbf{ }\mathbf{،}\mathbf{ }\frac{\mathbf{-}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٦}\mathbf{ }}{\mathbf{٢}}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{طول}\mathbf{ }\mathbf{نصف}\mathbf{ }\mathbf{القطر}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{{\mathbf{(}\mathbf{-}\mathbf{١}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{\left(}\mathbf{٣}\mathbf{\right)}}^{\mathbf{٢}}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{-}\mathbf{١٥}\mathbf{)}}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathbf{-}\mathbf{١}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{٢٥}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٥} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{طول}\mathbf{ }\mathbf{القطر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٢}\mathbf{\times }\mathbf{ }\mathbf{٥}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٠}\mathbf{ } \end{gathered}$$ 

  تدريب   $\left( \mathrm{٦} - \mathrm{١٧}\right)$  صفحة  $\mathbf{٦٠}$      

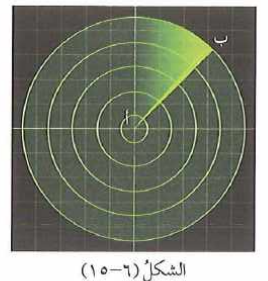
    النقطة ( أ ) في الشكل  $\left( \mathrm{٦} - \mathrm{١٥}\right)$ تمثل موقع رادار يرصد سيارة ( النقطة ب ) بحيث تبقى السيارة على بعد ثابت مقداره  $\left(\mathrm{٦٠}\right)$ كم عن الرادار 

               أ)  ما الشكل الهندسي الذي تتحرك عليه السيارة ؟               دائرة 

            ب)  ما معادلة المنحنى الذي تتحرك عليه السيارة ؟ ( معتبرًا النقطة  ( أ ) نقطة الأصل ) 

                                                         $\mathbf{ }\mathbf{ }\mathbf{ }{\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣٦٠٠}$                                                       

 

 

                                     تمارين و مسائل صفحة  $\mathbf{٦١}$

 

    

        $\mathbf{١}\mathbf{)}\mathbf{ }$  اكتب معادلة الدائرة في كل من الحالات الآتية : 

                   أ) مركزها نقطة الأصل و طول نصف قطرها  $\left(\mathrm{٢}\right)$ وحدة .                                                    ب) مركزها النقطة  $\left(-\mathrm{١} ، \mathrm{٣}\right)$ و طول قطرها  $\left(\mathrm{١٤}\right)$ وحدة . 

                                             $\mathbf{ }\mathbf{ }{\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٤}\mathbf{ }$                                                                                                  $$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٧} \\ \mathbf{ }\mathbf{ }{\left(س + \mathrm{١}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left(ص - \mathrm{٣}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٤٩}\mathbf{ } \end{gathered}$$       

 

                 ج) مركزها النقطة  $\left( \mathrm{٤} ، -\mathrm{١}\right)$ و تمر بالنقطة    $\mathbf{(}\mathbf{ }\mathbf{٩}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٢}\mathbf{)}$ .                                         د)  مركزها النقطة  $\left(\mathrm{٥} ، \mathrm{٣}\right)$ ، و تمس محور السينات 

                             $$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{{\mathbf{(}\mathbf{٩}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٤}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{-}\mathbf{٢}\mathbf{ }\mathbf{-}\mathbf{-}\mathbf{١}\mathbf{)}}^{\mathbf{٢}}}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{٢٥}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١}\mathbf{ }}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{٢٦}}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٤}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{ص}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٢٦} \end{gathered}$$                                                                               $$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{تمس}\mathbf{ }\mathbf{محور}\mathbf{ }\mathbf{السينات}\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }{\left( س - \mathrm{٥}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left( ص - \mathrm{٣}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩}\mathbf{ } \end{gathered}$$

 

              هـ) طول قطرها  $\left(\mathrm{٦}\right)$ وحدات و تمس كلا من محور السينات و محور الصادات ( جد جميع الحلول الممكنه) 

                               

$$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{حالة}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{حالة}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{حالة}\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{حالة}\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{)}\mathbf{ } \\ \mathbf{المركز}\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{،}\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ا}\mathbf{لمركز}\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{،}\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{المركز}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{-}\mathbf{٣}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٣}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{،}\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{المركز}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{-}\mathbf{٣}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{،}\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \\ \mathbf{ } \\ {\mathbf{(}\mathbf{ }\mathbf{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٣}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{ص}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٣}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }{\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{س}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٣}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{ص}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٣}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{(}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{(}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{)} \end{gathered}$$                               

                      

$\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{٢}\mathbf{)}$ جد إحداثيي المركز وطول نصف قطر الدائرة التي معادلتها : 

             $$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{ }\mathit{أ}\mathbf{)}\mathbf{ }\mathbf{ }{\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٢١}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{المركز}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٠}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{٠}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{،}\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١١} \end{gathered}$$                                                                 $$\begin{gathered} \mathit{ب}\mathbf{)}\mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left( س + \mathrm{٤} \right)}^{\mathrm{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٨}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{المركز}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{،}\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{١٨}} \end{gathered}$$     

 

                $$\begin{gathered} \mathit{ج}\mathbf{)}\mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{٣}\mathit{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٦}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left(\mathrm{٣} ص + \mathrm{١٢}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣٦}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }{\mathbf{\left(}\mathbf{٣}\left(س - \mathrm{٢}\right)\mathbf{\right)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{\left(}\mathbf{٣}\left( ص + \mathrm{٤}\right)\mathbf{\right)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣٦}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{٩}\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٩}\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣٦}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left( ص + \mathrm{٤}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٤}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{المركز}\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٤}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{،}\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٢}\mathbf{ } \end{gathered}$$

 

                 $$\begin{gathered} \mathit{د}\mathbf{)}\mathbf{ }{\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٤}\mathit{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{١٠}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٢٨}\mathbf{ } \\ \mathbf{\leftarrow }\mathbf{ }{\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٤}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١٠}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٢٨}\mathbf{ } \\ \mathbf{\leftarrow }\mathbf{ }{\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٤}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١٠}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٢٥}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٢٨}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٢٥} \\ \mathbf{\leftarrow }{\left(س - \mathrm{٢}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left( ص + \mathrm{٥} \right)}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١}\mathbf{ } \\ \mathbf{ }\mathbf{المركز}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٥}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{،}\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١}\mathbf{ } \end{gathered}$$                                                  $$\begin{gathered} \mathbf{ }\mathit{ه}\mathit{ـ}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }{\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٨}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٢}\mathbf{ } \\ \mathbf{\leftarrow }\mathbf{ }{\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٨}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٢}\mathbf{ } \\ \mathbf{\leftarrow }\mathbf{ }{\mathit{س}}^{\mathbf{٢}}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٨}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١٦}\mathbf{ }\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٢}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١٦}\mathbf{ } \\ \mathbf{\leftarrow }\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٤}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{ص}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٢٨}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{المركز}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{٠}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{،}\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{٢٨}} \end{gathered}$$

 

 

      $\mathbf{٣}\mathbf{)}$   حدد موقع كل نقطة من النقاط الاتية بالنسبة للدائرة التي معادلتها  $\mathbf{ }{\mathbf{(}\mathbf{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٥}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{ص}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩}$

         

       $$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ن}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{و}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{٠}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ل}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{-}\mathbf{٢}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ك}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٥}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{-}\mathbf{١}\mathbf{ }\mathbf{)} \\ \mathbf{\leftarrow }\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٥}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left(-\mathrm{١} + \mathrm{١}\right)}^{\mathrm{٢}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٥}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{٠}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٥}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left(-\mathrm{٢} + \mathrm{١}\right)}^{\mathrm{٢}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{٥}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٥}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left(-\mathrm{١} + \mathrm{١}\right)}^{\mathrm{٢}}\mathbf{}\mathbf{\leftarrow }\mathbf{ }\mathbf{٩}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٠}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{ }\mathbf{١٦}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٧}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{=}\mathbf{٢}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{٠}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٠}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٠} \\ \mathbf{\leftarrow }\mathbf{٩}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{ }\mathbf{١٧}\mathbf{ }\mathbf{>}\mathbf{ }\mathbf{٩}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{ }\mathbf{٢}\mathbf{<}\mathbf{ }\mathbf{٩}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{٠}\mathbf{<}\mathbf{ }\mathbf{٩}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{تقع}\mathbf{ }\mathbf{على}\mathbf{ }\mathbf{الدائرة}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{خارج}\mathbf{ }\mathbf{الدائرة}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{داخل}\mathbf{ }\mathbf{الدائرة}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{داخل}\mathbf{ }\mathbf{الدائرة}\mathbf{ } \end{gathered}$$                 

 

  $\mathbf{٤}\mathbf{)}$  ما معادلة الدائرة التي مركزها النقطة  $\left(\mathrm{٤} ، \mathrm{١}\right)$ و تمس المستقيم الذي معادلته  $\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{-}\mathbf{٢}$ ؟ 

             $$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{طول}\mathbf{ }\mathbf{نصف}\mathbf{ }\mathbf{القطر}\mathbf{ }\mathbf{يساوي}\mathbf{ }\mathbf{بعد}\mathbf{ }\mathbf{ }\mathbf{المركز}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{١}\mathbf{)}\mathbf{ }\mathbf{عن}\mathbf{ }\mathit{ا}\mathbf{لمستقيم}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٢}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{{\left(\mathrm{٤} - \mathrm{٤}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left(\mathrm{١} - - \mathrm{٢}\right)}^{\mathbf{٢}}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{٠}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{٩}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left( ص - \mathrm{١}\right)}^{\mathrm{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩}\mathbf{ } \end{gathered}$$

 

 

$\mathbf{ }\mathbf{٥}\mathbf{)}$ ما معادلة الدائرة التي يقع مركزها على المستقيم الذي معادلته  $\mathbf{ }\mathit{س}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٥}\mathbf{ }$ ، و تمس محور الصادات عند النقطة  $\left(\mathrm{٠} ، \mathrm{٣}\right)$ ؟ 

 

                           $$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{المركز}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٥}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{،}\mathbf{ }\mathit{ر}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٥} \\ \mathbf{ }\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٥}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٣}\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{٢٥} \end{gathered}$$