تدريب صفحة
جد معادلة الخط المستقيم الذي ميله و يمر بنقطة الأصل .
تدريب صفحة
جد معادلة المستقيم المار بالنققطتين
تدريب صفحة
يسير قطار من المدينة أ الى المدينة ب بسرعة منتظمة و يقف عند كل محطة بين المدينتين ، يبين الجدول الاتي رقم المحطة (ن) و المدة الزمنية للرحلة (س) ساعة و بعد المحطة عن
المدينة أ (ص) كم :
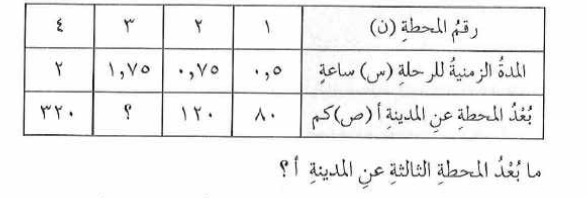
تدريب صفحة
ما معادلة الخط المستقيم الذي ميله ، و مقطعه السيني
تمارين و مسائل صفحة
أي النقاط الاتية تقع على الخط المستقيم الذي معادلته
النقاط التي تقع على الخط المستقيم : النقطة ب ، النقطة ج ، النقطة د ، النقطة و .
اكتب معادلة الخط المستقيم في كل حالة من الحالات الاتية :
أ) ميله ، و يمر بالنقطتين ب) يمر بالنقطتين
ج) ميله و مقطعه السيني د) ميله ، و مقطعه الصادي
هـ) مقطعه السيني ، ومقطعه الصادي . و) يوازي محور السينات و مقطعه الصادي
جد إحداثيي نقطة تقاطع المستقيم الذي معادلته مع محور السينات .
يقطع المستقيم محور السينات عندما
جد إحداثيي نقطة تقاطع المستقيم الذي معادلته مع محور الصادات .
يقطع المستقيم محور الصادات عندما
جد كلا من المقطع السني و المقطع الصادي للمستقيم الذي معادلته
المقطع السيني المقطع الصادي
ما معادلة المستقيم الذي ، و يمر بنقطة تقاطع المستقيم الذي معادلتة مع محور الصادات
يقطع المستقيم محور الصادات عندما
إذا كان المستقيم ل يمر بالنقطتين و ميله ، فأجب عمايأتي :
أ) ماقيمة الثابت ك ؟
ب) ما معادلة المستقيم ل ؟
جد إحداثيي نقطة تقاطع المستقيم الذي معادلته مع المستقيم الذي معادلته
جد إحداثيي نقطة تقاطع المستقيم الذي معادلته ، مع المستقيم الذي معادلته
إذا كانت النقطتان ، وكان المستقيمان أج ، ب ج متقاطعين في النقطة ج ، و كان ميلاهما ، ما احداثيات النقطة ج ؟
نفرض أن احداثيات النقطة ج ( س ، ص )
ميل المستقيم أ ج = ميل المستقيم ب ج =
إذا كانت النقاط نقاطًا في المستوى الاحداثي ، فجد :
أ) معادلة المستقيم ن هـ
ب) معادلة المستقيم ك و
ج) نقطة تقاطع المستقيمين ن هـ ، ك و إن وجدت .
لا يوجد نقاط تقاطع
