معادلةُ المستقيمِ بصيغةِ المَيلِ والمقطعِ

تعلّمْتُ سابقًا كيفيّةَ إيجادِ الميلِ والمقطعينِ الإحداثيّينِ للمستقيمِ. ويمكِنُني استعمالُ المَيلِ والمقطعِ y لكتابةِ معادلةِ أيِّ مستقيمٍ بصيغةِ الميلِ والمقطعِ 

صيغةُ المَيلِ والمقطعِ:

مثال(1)

أكتبُ معادلةَ المستقيمِ الذي ميلُه $\frac{4}{5}$ والمقطعُ y لهُ $-7$ بصيغةِ الميلِ والمقطعِ.

أعوّضُ المَيلَ والمقطعَ y في صيغةِ المَيلِ والمقطعِ

$$\begin{gathered} y=mx+b \\ y= \frac{4}{5}x + (-7) \\ y=\frac{4}{5}x -7 \end{gathered}$$

2) أجدُ معادلةَ المستقيمِ المارِّ بالنقطةِ ( 5 , 1) وميلُه 2 بصيغةِ الميلِ والمقطعِ.

الْخُطْوَةُ 1:  استعمل الميلَ وإحداثيَّيِ النقطةِ لإيجادِ قيمةِ b.

$$\begin{gathered} y=mx+b \\ y= 2x +b \\ 5=2\left(1\right) +b \\ b=3 \end{gathered}$$

الْخُطْوَةُ 2: أعوّضُ الميلَ والمقطعَ y في صيغةِ الميلِ والمقطعِ.

$$\begin{gathered} y=mx+b \\ y= 2x +3 \end{gathered}$$

3) أكتبُ معادلةَ المستقيمِ المارِّ بالنقطتينِ $( 5 , -8) ,( 2, 1)$ بصيغةِ الميلِ والمقطعِ.

الْخُطْوَةُ 1: استعمل النقطتينِ في إيجادِ المَيلِ.

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{-8-1}{5-2}=\frac{-9}{3}=-3$

الْخُطْوَةُ 2: استعمل الميلَ وإحداثيَّي إحدى النقطتينِ لإيجادِ قيمةِ b

$$\begin{gathered} y=mx+b \\ y= -3x +b \\ 1=-3\left(2\right) +b \\ 1=-6+b \\ b=7 \end{gathered}$$

الْخُطْوَةُ 3: أعوّضُ المَيلَ والمقطعَ y في صيغةِ المَيلِ والمقطعِ.

$$\begin{gathered} y=mx+b \\ y= -3x +7 \end{gathered}$$

يمكنُ استعمالُ الميلِ والمقطعِ y منَ المعادلةِ الخطّيةِ المكتوبةِ بصيغةِ الميلِ والمقطعِ لتمثيلِ المستقيمِ.

 

مثال(2) 

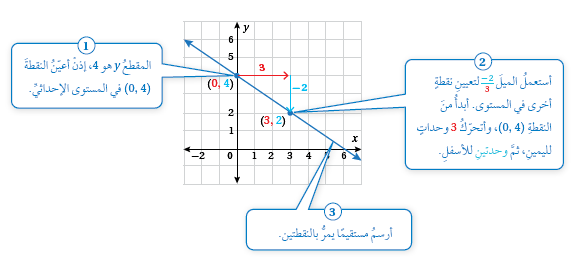
أمثّلُ المعادلةَ $y=\frac{2}{3}x+4$ بيانيًّا باستعمالِ الميلِ والمقطعِ$y$ .

يُمكِن كتابةُ معادلةِ مستقيمٍ بصيغةِ الميلِ والمقطعِ عُرِفَ تمثيلُها البيانيُّ.

مثال(3) 

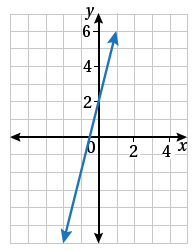
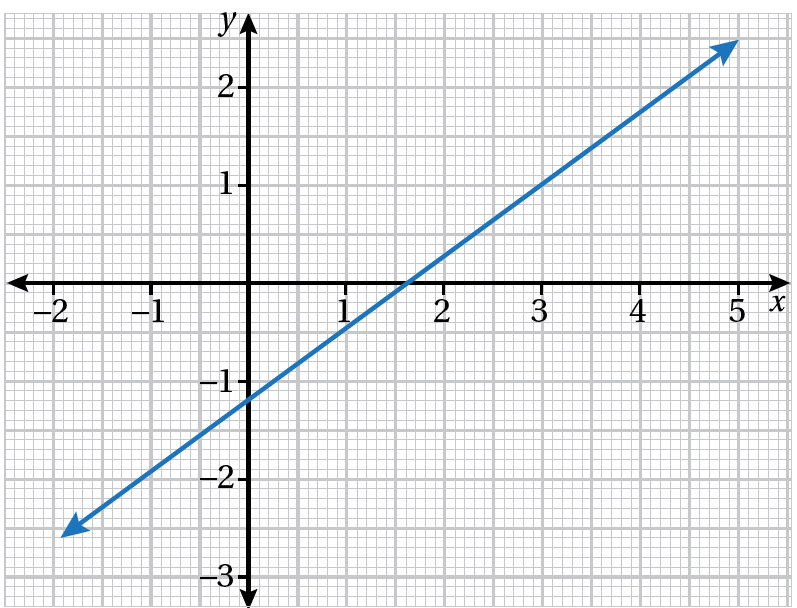
أكتبُ معادلةَ المستقيمِ المُمَثَّلةَ بيانيًّا في الشكلِ المجاورِ  
بصيغةِ الميلِ والمقطعِ:

الْخُطْوَةُ 1: أجدُ المقطعَ $y$.
أُلاحظُ أنَّ المستقيمَ قطعَ المحورَ y عندَ 2، إذنْ، فالمقطعُ y هو 2

الْخُطْوَةُ 2: أجدُ الميلَ.

$$\begin{gathered} (-1, -2), (0, 2) \\ m=\frac{y_2-y_1}{x_2-x_1}=\frac{2--2}{0--1}=\frac{4}{1}=1 \end{gathered}$$

الْخُطْوَةُ 3: اكتب معادلةً 

أعوّضُ الميلَ والمقطعَ y في صيغةِ الميلِ والمقطعِ.

$$\begin{gathered} y=mx+b \\ y= 4x +2 \end{gathered}$$

مثال(4) 

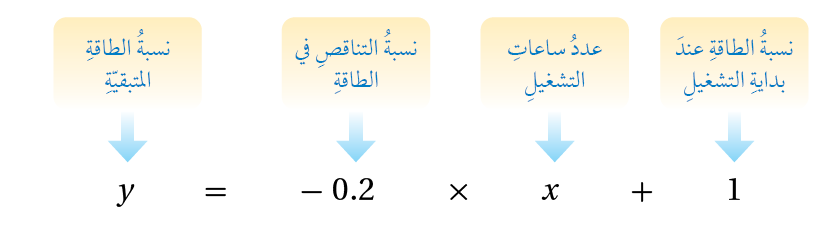
بطاريةٌ: إذا كانتِ النسبةُ المئويةُ لطاقةِ بطاريةِ جهازِ حاسوبٍ محمولٍ مشحونةٍ شحنًا تامًّا (بالصيغةِ العشريةِ) 1.00، وبعدَ تشغيلِ الجهازِ تبدأُ طاقةُ البطاريةِ بالتناقُصِ بنسبةِ 0.2 كلَّ ساعةٍ.

1) أكتبُ معادلةً خطّيةً بمتغيرينِ لإيجادِ نسبةِ الطاقةِ المتبقيّةِ في البطاريةِ بعدَ مرورِ ساعاتٍ عدّةٍ على تشغيلِ جهازِ الحاسوبِ.
 

افرض أنَّ x هيَ عددُ ساعاتِ تشغيلِ الحاسوبِ، و y هيَ نسبةُ الطاقةِ المتبقيةِ في البطاريةِ.

2) أصفُ ما يمثلُّه المقطعُ y والمَيلُ في المسألةِ. 

المقطعُ y يساوي 1، وهو يمثلُ نسبةَ الطاقةِ بدايةَ التشغيلِ بالصيغةِ العشريةِ، وتعني أنَّ البطاريةَ مشحونةٌ بنسبةِ % 100 ، أمّا المَيلُ فيمثلُ نسبةَ التناقُصِ في طاقةِ البطاريةِ كلَّ ساعةٍ  وهي نسبةٌ ثابتةٌ.

3) أجدُ المقطعَ x للمعادلةِ، ثمَّ أصفُ ما يمثلُه في المسألةِ.

لإيجادِ المقطعِ x، أعوّضُ y = 0 ، ثمَّ أحلُّ المعادلةَ لأجدَ قيمةَ x 

$$\begin{gathered} y=-0.2x+1 \\ 0=-0.2x+1 \\ 0.2x=1 \\ x=\frac{1}{0.2} \\ x=5 \end{gathered}$$

إذنْ، فالمقطعُ x هو 5، وهو يدلُّ على أنَّ البطاريةَ ستفقدُ شحنَها كليًّا بعدَ 5 ساعاتٍ منْ تشغيلِ جهازِ الحاسوبِ.

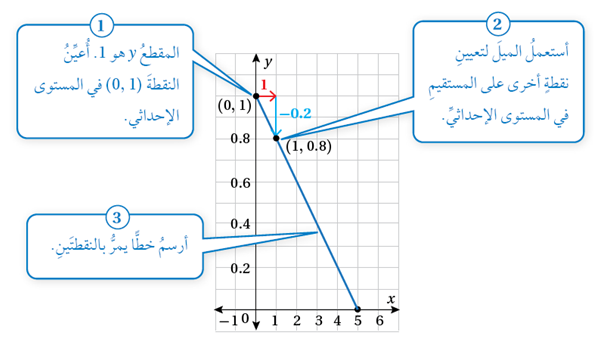
4)أمثّلُ المعادلةَ بيانيًّا باستعمالِ المَيلِ والمقطعِ y 

5) بعدَ كمْ ساعةٍ تكونُ نسبةُ الطاقةِ في البطاريةِ 0.75؟

$$\begin{gathered} y=-0.2x+1 \\ 0.75= -0.2x+1 \\ 0.75-1 =-0.2x \\ -0.25 = -0.2x \\ \frac{-0.2x}{-0.2}=\frac{-0.25}{-0.2} \\ x= 1.25 \end{gathered}$$

إذنْ، ستكونُ نسبةُ الطاقةِ في البطاريةِ 0.75 بعدَ ساعةٍ وربعٍ.

مثال(5)

يبيّنُ الشكلُ المجاورُ التمثيلَ البيانيَّ للمعادلةِ $y = 0.73x - 1.15$ استعمل التمثيلَ البيانيَّ لأجدَ حلَّ كلِّ معادلةٍ ممّا يأتي:

$\mathbf{1}\mathbf{)}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{73}\mathit{x}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{1}\mathbf{.}\mathbf{15}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}$

بما أن المعادلةُ $y = 0.73x-1.15$ ، فإنَّ$0.73x-1.15=0$ عندَما تكونُ قيمةُ y تساوي صفرًا، ويقطعُ عندَها المستقيمُ المُمثِّلُ للمعادلةِ المحورَ $x$ ومنْ قراءةِ التمثيلِ البيانيِّ أجدُ أنَّ 

إذنْ، حلُّ المعادلةِ هوَ $x = 1.6$

$\mathbf{2}\mathbf{)}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{73}\mathit{x}\mathbf{-}\mathbf{1}\mathbf{.}\mathbf{15}\mathbf{=}\mathbf{-}\mathbf{2}\mathbf{.}\mathbf{2}$ 

لحلِّ المعادلةِ أجدُ $-2.2$ على المحورِ $y$، ثمَّ أحدّدُ النقطةَ التي تقابلُها على الخطِّ المستقيمِ، وأحدّدُ الإحداثيَّ $x$ للنقطةِ وهوَ $-1.4$

إذنْ، حلُّ المعادلةِ $x = -1.4$

$3) 0.73x-3.05=0$

بما أن المعادلةُ $0.73x - 3.05=0$، فهيَ ناتجةٌ عنْ $0.73x-1.15-1.9=0$ ،وعليهِ فإنَّهُ يمكنُ إعادةُ كتابةِ المعادلةِ على الصورةِ: $0.73x - 1.15 = 1.9$

ولحلِّ المعادلةِ أجدُ 1.9 على المحورِ $y$، ثمَّ أحدّدُ النقطةَ التي تقابلُها على المستقيمِ، وأحدّدُ الإحداثيَّ $x$ للنقطةِ وهوَ 4.2 .

إذنْ، حلُّ المعادلةِ $x = 4.2$