رياضيات فصل ثاني

حلول أسئلة أتحقق من فهمي 

2)

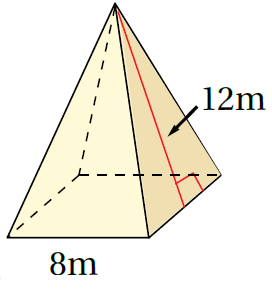
الْخُطْوَةُ 1: أَجِدُ محيطَ القاعدةِ وَمساحتَها: 

P = 4 × 8 = 32                القاعدة مربعة p = 4 × s

B = 8² = 64                    مساحةُ القاعدةِ B=s²

الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ الهَرَمِ :

          $\mathrm{L}.\mathrm{A}=\frac{1}{2}\mathrm{Pl}$             صيغةُ المساحةِ الجانبيةِ لِسطحِ الهَرَمِ

$$\begin{gathered} =\frac{1}{2}\left(32\right)\left(12\right) \\ =192 \end{gathered}$$              بتعويض الأبعاد نجد الناتج 

إذنْ، المساحةُ الجانبية لِسطحِ الهَرَمِ تساوي 192m²

الْخُطْوَةُ 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ الهَرَمِ :

S.A = L.A + B                  صيغةُ المساحةِ الكلّيةِ لِسطحِ الهَرَمِ

192+64 =                        بتعويض الأبعاد نجد الناتج 

       256=

إذنْ، المساحةُ الكلّيةُ لِسطحِ الهَرَمِ تساوي 256m²

 

3)

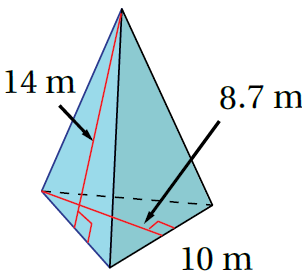
الْخُطْوَةُ 1: أَجِدُ محيطَ القاعدةِ وَمساحتَها: 

P = 10+10+10 = 30         القاعدة مثلث 

$$\begin{gathered} \mathrm{B}=\frac{1}{2}\left(10\right)\left(8.7\right) \\ =43.5 \end{gathered}$$              مساحةُ القاعدةِ (مثلث)

الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ الهَرَمِ :

           $\mathrm{L}.\mathrm{A}=\frac{1}{2}\mathrm{Pl}$            صيغةُ المساحةِ الجانبيةِ لِسطحِ الهَرَمِ

$$\begin{gathered} =\frac{1}{2}\left(30\right)\left(14\right) \\ =210 \end{gathered}$$            بتعويض الأبعاد نجد الناتج 

 إذنْ، المساحةُ الجانبيةُ لِسطحِ الهَرَمِ تساوي 210m²

الْخُطْوَةُ 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ الهَرَمِ :

    S.A = L.A + B              صيغةُ المساحةِ الكلّيةِ لِسطحِ الهَرَمِ

210+43.5 =                     بتعويض الأبعاد نجد الناتج 

      253.5 =

إذنْ، المساحةُ الكلّيةُ لِسطحِ الهَرَمِ تساوي 253.5m²

 

خيمةٌ: صمّمَ ينالٌ الهَرَمَ المجاورَ الّذي يمثّلُ الأعمدةَ الأساسيةَ لِنموذجِ خيمةٍ، ما مساحة القماش التي يحتاجها لإكمال النموذج وتغطية الأعمدة

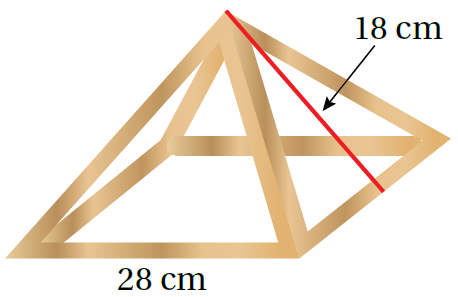
مساحة القماش = المساحة الجانبية لسطح الهرم 

الْخُطْوَةُ 1: أَجِدُ محيطَ القاعدةِ : 

P = 4 × 28 = 112             القاعدة مربعة p = 4 × s

الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ الهَرَمِ :

             $\mathrm{L}.\mathrm{A}=\frac{1}{2}\mathrm{Pl}$          صيغةُ المساحةِ الجانبيةِ لِسطحِ الهَرَمِ

$$\begin{gathered} =\frac{1}{2}\left(112\right)\left(18\right) \\ =1008{\mathrm{cm}}^2 \end{gathered}$$         بتعويض الأبعاد نجد الناتج 

مساحة القماش التي يحتاجها ينال لإكمال النموذج وتغطية الأعمدة هي 1008cm²

---

2)

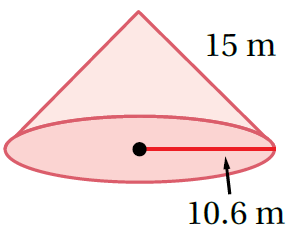
الْخُطْوَةُ 1: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المخروطِ: 

             $\mathrm{L}.\mathrm{A}=\mathrm{\pi r\ell }$        صيغةُ المساحةِ الجانبيةِ لِسطحِ المخروطِ

$$\begin{gathered} =\mathrm{\pi }(10.6)\left(15\right) \\ \approx 499.5 \end{gathered}$$              بتعويض الأبعاد نجد الناتج

إذنْ، المساحةُ الجانبيةُ لِسطحِ المخروطِ تساوي499.5m²

الْخُطْوَةُ 2 : أَجِدُ مساحةَ القاعدةِ:      

         B = πr²                صيغةُ مساحةِ الدائرةِ 

 π(10.6²)=                    بتعويض نصف القطر نجد الناتج 

≈  353       

إذنْ، مساحةُ القاعدةِ 353m²

الْخُطْوَةُ 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ المخروطِ:

         S.A = L.A + B            صيغةُ مساحةِ سطحِ المخروطِ 

  499.5+353 =                   بتعويض الابعاد نجد الناتج

          852.5 =

 إذنْ، المساحةُ الكلّيةُ لِسطحِ المخروطِ تساوي 852.5m² تقريباً 

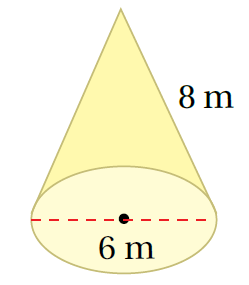
3)

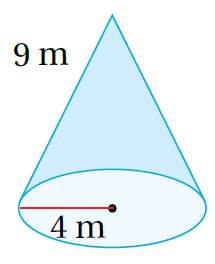
الْخُطْوَةُ 1: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المخروطِ: 

           $\mathrm{L}.\mathrm{A}=\mathrm{\pi r\ell }$           صيغةُ المساحةِ الجانبيةِ لِسطحِ المخروطِ

     $$\begin{gathered} =\mathrm{\pi }\left(4\right)\left(9\right) \\ \approx 113.1 \end{gathered}$$                  بتعويض الأبعاد نجد الناتج

إذنْ، المساحةُ الجانبيةُ لِسطحِ المخروطِ تساوي113.1m²

الْخُطْوَةُ 2 : أَجِدُ مساحةَ القاعدةِ:      

     B = πr²                     صيغةُ مساحةِ الدائرةِ 

  π(4²)=                        بتعويض نصف القطر نجد الناتج 

≈ 50.3  

إذنْ، مساحةُ القاعدةِ 50.3m²

الْخُطْوَةُ 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ المخروطِ:

         S.A = L.A + B            صيغةُ مساحةِ سطحِ المخروطِ 

   113.1+50.3 =                   بتعويض الابعاد نجد الناتج

           163.4 =

 إذنْ، المساحةُ الكلّيةُ لِسطحِ المخروطِ تساوي 163.4m² تقريباً 

 

مخروطُ مرورٍ : مخروطُ مرورٍ طولُ نصفِ قُطرِ قاعدتِهِ 25cm وَارتفاعُهُ الجانبيُّ 75cm أَجِدُ المساحةَ الجانبيةَ لِسطحِ المخروطِ. أقرّبُ إجابتي لِأقربِ عددٍ صحيحٍ. 

             L.A = πrℓ              صيغةُ المساحةِ الجانبيةِ لِسطحِ المخروطِ

π (25)(75) =                      بتعويض الأبعاد نجد الناتج 

     5890.4 ≈ 

إذنْ، مساحةُ ورقِ الترشيحِ تساوي 5890cm²  تقريبًا. 

---

---

حلول أسئلة أتدرب وأحل المسائل 

أَجِدُ المساحةَ الكلّيةَ لِسطحِ كلِّ هَرَمٍ منتظَمٍ ممّا يأتي:

1)

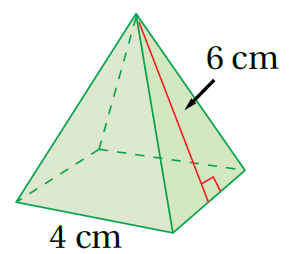
الْخُطْوَةُ 1: أَجِدُ محيطَ القاعدةِ وَمساحتَها: 

P = 4 × 4 = 16                القاعدة مربعة p = 4 × s

B = 4² = 16                    مساحةُ القاعدةِ B=s²

الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ الهَرَمِ :

             $\mathrm{L}.\mathrm{A}=\frac{1}{2}\mathrm{Pl}$          صيغةُ المساحةِ الجانبيةِ لِسطحِ الهَرَمِ

    $$\begin{gathered} =\frac{1}{2}\left(16\right)\left(6\right) \\ =48{\mathrm{cm}}^2 \end{gathered}$$          بتعويض الابعاد نجد الناتج

الْخُطْوَةُ 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ الهَرَمِ :

S.A = L.A + B                 صيغةُ المساحةِ الكلّيةِ لِسطحِ الهَرَمِ

 48+16 =                        بتعويض الأبعاد نجد الناتج 

 64cm² = 

 

2)

 

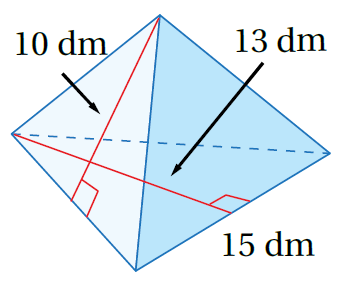
الْخُطْوَةُ 1: أَجِدُ محيطَ القاعدةِ وَمساحتَها: 

P = 15+15+15 = 45         القاعدة مثلث 

$$\begin{gathered} \mathrm{B}=\frac{1}{2}\left(15\right)\left(13\right) \\ =97.5 \end{gathered}$$               مساحة القاعدة المثلثية

الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ الهَرَمِ :

             $\mathrm{L}.\mathrm{A}=\frac{1}{2}\mathrm{Pl}$          صيغةُ المساحةِ الجانبيةِ لِسطحِ الهَرَمِ

  $$\begin{gathered} =\frac{1}{2}\left(45\right)\left(10\right) \\ =225 {\mathrm{dm}}^2 \end{gathered}$$          بتعويض الابعاد نجد الناتج

الْخُطْوَةُ 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ الهَرَمِ :

     S.A = L.A + B            صيغةُ المساحةِ الكلّيةِ لِسطحِ الهَرَمِ

225+97.5 =                    بتعويض الأبعاد نجد الناتج 

$=322.5{\mathrm{dm}}^2$

 

أَجِدُ المساحةَ الكلّيةَ لِسطحِ كلِّ مخروطٍ ممّا يأتي: 

3) 

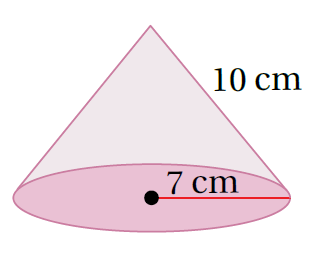
الْخُطْوَةُ 1: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المخروطِ: 

        $\mathrm{L}.\mathrm{A}=\mathrm{\pi r\ell }$              صيغةُ المساحةِ الجانبيةِ لِسطحِ المخروطِ

$$\begin{gathered} =\mathrm{\pi }\left(7\right)\left(10\right) \\ \approx 220 \end{gathered}$$                     بتعويض الأبعاد نجد الناتج 

الْخُطْوَةُ 2 : أَجِدُ مساحةَ القاعدةِ:      

     B = πr²                     صيغةُ مساحةِ الدائرةِ 

  π(7²)=                        بتعويض نصف القطر نجد الناتج 

≈ 154    

الْخُطْوَةُ 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ المخروطِ:

         S.A = L.A + B            صيغةُ مساحةِ سطحِ المخروطِ 

      220+154 =                   بتعويض الابعاد نجد الناتج

       ${\approx 374\mathrm{cm}}^2$

 

4) 

الْخُطْوَةُ 1: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المخروطِ: 

      $\mathrm{L}.\mathrm{A}=\mathrm{\pi r\ell }$                صيغةُ المساحةِ الجانبيةِ لِسطحِ المخروطِ

$$\begin{gathered} =\mathrm{\pi }\left(3\right)\left(8\right) \\ \approx 75.4 \end{gathered}$$                        بتعويض الأبعاد نجد الناتج 

الْخُطْوَةُ 2 : أَجِدُ مساحةَ القاعدةِ:      

     B = πr²                     صيغةُ مساحةِ الدائرةِ 

  π(3²)=                        بتعويض نصف القطر نجد الناتج 

$\approx$28.3  

الْخُطْوَةُ 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ المخروطِ:

         S.A = L.A + B            صيغةُ مساحةِ سطحِ المخروطِ 

   75.4+28.3 =                   بتعويض الابعاد نجد الناتج

    $=103.7 {\mathrm{m}}^2$

 

أَجِدُ المساحةَ الكلّيةَ لِسطحِ كلِّ مجسَّمٍ ممّا يأتي: 

5) هَرَمٌ رباعيٌّ منتظَمٌ طولُ قاعدتِهِ 5m وَارتفاعُهُ الجانبيُّ 6m

الْخُطْوَةُ 1: أَجِدُ محيطَ القاعدةِ وَمساحتَها: 

P = 4 × 5 = 20                القاعدة مربعة p = 4 × s

B = 5² = 25                     مساحةُ القاعدةِ B=s²

الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ الهَرَمِ :

             $\mathrm{L}.\mathrm{A}=\frac{1}{2}\mathrm{Pl}$          صيغةُ المساحةِ الجانبيةِ لِسطحِ الهَرَمِ

    $$\begin{gathered} =\frac{1}{2}\left(20\right)\left(6\right) \\ =60{\mathrm{m}}^2 \end{gathered}$$            بتعويض الأبعاد نجد الناتج

الْخُطْوَةُ 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ الهَرَمِ :

S.A = L.A + B                  صيغةُ المساحةِ الكلّيةِ لِسطحِ الهَرَمِ

60+25 =                        بتعويض الأبعاد نجد الناتج 

$=85{\mathrm{m}}^2$

 

6) مخروطٌ طولُ نصفِ قُطرِ قاعدتِهِ 16m وَارتفاعُهُ الجانبيُّ 28m 

الْخُطْوَةُ 1: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المخروطِ: 

      $\mathrm{L}.\mathrm{A}=\mathrm{\pi r\ell }$                صيغةُ المساحةِ الجانبيةِ لِسطحِ المخروطِ

$$\begin{gathered} =\mathrm{\pi }\left(16\right)\left(28\right) \\ \approx 1407.4 \end{gathered}$$                 بتعويض الأبعاد نجد الناتج 

الْخُطْوَةُ 2 : أَجِدُ مساحةَ القاعدةِ:      

     B = πr²                     صيغةُ مساحةِ الدائرةِ 

  π(16²)=                       بتعويض نصف القطر نجد الناتج 

≈ 804.25

الْخُطْوَةُ 3: أَجِدُ المساحةَ الكلّيةَ لِسطحِ المخروطِ:

           S.A = L.A + B    صيغةُ مساحةِ سطحِ المخروطِ 

1407.4+804.3 =           بتعويض الابعاد نجد الناتج

       $=2211.7{\mathrm{m}}^2$

 

7) مصباحُ طاولةٍ: قاعدةُ غطاءِ مصباحِ الطاولةِ المجاورِ على شكلِ هَرَمٍ سُداسيٍّ منتظَمٍ طولُ ضِلعِهِ 8in ،أقدّرُ مساحةَ الزجاجِ اللازمةَ لِصنعِ الغطاءِ.

مساحة الزجاج = المساحة الجانبية للهرم السداسي 

الْخُطْوَةُ 1: أَجِدُ محيطَ القاعدةِ : 

P = 6 × 8 = 48                القاعدة سداسية p = 6 × s

الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ الهَرَمِ :

          $\mathrm{L}.\mathrm{A}=\frac{1}{2}\mathrm{Pl}$          صيغةُ المساحةِ الجانبيةِ لِسطحِ الهَرَمِ

$$\begin{gathered} =\frac{1}{2}\left(48\right)\left(10\right) \\ =240{\mathrm{in}}^2 \end{gathered}$$          بتعويض الابعاد نجد الناتج

 

أَجِدُ المساحةَ الكلّيةَ لِسطحِ كلِّ مجسَّمٍ ممّا يأتي:

8) 

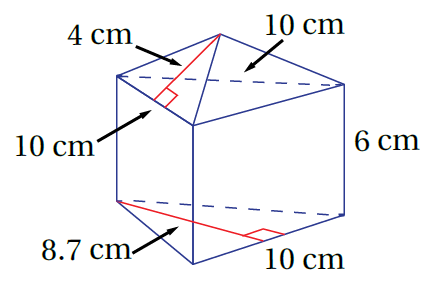
لاحظ بأن الشكل يتكون من هرم مفتوح على منشور ثلاثي 

المساحة الكلية للمجسم = مساحة الهرم الجانبية +(مساحة المنشور الثلاثي الجانبية+ مساحة القاعدة) 

$$\begin{gathered} \mathrm{S}.\mathrm{A}=\mathrm{L}.{\mathrm{A}}_{\mathrm{الهرم}}+\mathrm{L}.{\mathrm{A}}_{\mathrm{المنشور} }+{\mathrm{A}}_{ △\mathrm{القاعدة} } \\ =\frac{1}{2}\mathrm{PL} + \mathrm{Ph} +{\mathrm{A}}_{\mathrm{المثلث}} \end{gathered}$$

محيط قاعدة الهرم = محيط قاعدة المنشور :

$$\begin{gathered} \mathrm{P}=10+10+10 \\ =30 \end{gathered}$$

مساحة القاعدة _المثلثA:

$$\begin{gathered} \mathrm{A}=\frac{1}{2}\left(10\right)\left(8.7\right) \\ =43.5 \end{gathered}$$

بالتعويض في الصيغة الرئيسية للمساحة الكلية للمجسم : 

$$\begin{gathered} \mathrm{S}.\mathrm{A}=\frac{1}{2}\mathrm{PL} + \mathrm{Ph} +{\mathrm{A}}_{\mathrm{المثلث}} \\ =\frac{1}{2}\left(30\right)\left(4\right)+\left(30\right)\left(6\right)+43.5 \\ =283.5 {\mathrm{cm}}^2 \end{gathered}$$

 

9)

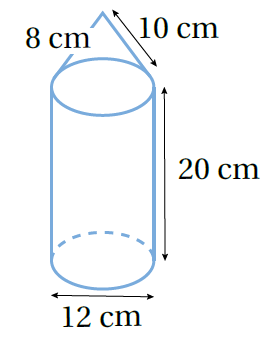
لاحظ بأن الشكل يتكون من مخروط مفتوح على أسطوانة 

المساحة الكلية للمجسم = مساحة الأسطوانة الجانبية + مساحة المخروط الجانبية + مساحة القاعدة 

$$\begin{gathered} \mathrm{S}.\mathrm{A}=\mathrm{L}.{\mathrm{A}}_{\mathrm{المخروط}}+\mathrm{L}.{\mathrm{A}}_{\mathrm{الأسطوانة}}+{\mathrm{A}}_{\mathrm{القاعدة} ○} \\ =\mathrm{\pi r\ell } +2\mathrm{\pi rh} +{\mathrm{\pi r}}^2 \\ =\mathrm{\pi r}\left(\mathrm{\ell }+2\mathrm{h}+\mathrm{r}\right) \end{gathered}$$           بأخذ $\mathbf{\pi r}$ كعامل مشترك 

بتعويض الأبعاد ،أجد الناتج :

$$\begin{gathered} =6\mathrm{\pi }\left(10+2\left(20\right)+6\right) \\ =6\mathrm{\pi }\left(56\right) \\ \approx 1055.6{\mathrm{cm}}^2 \end{gathered}$$

 

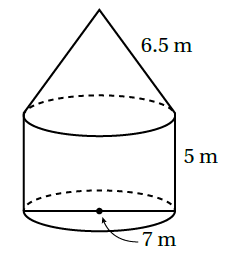
10) أقماعٌ: صُنِّعَ القُمعانِ المجاورانِ مِنَ البلاستيكِ، أَجِدُ الفرقَ بينَ مساحتَيِ البلاستيكِ المستخدَمةِ في صُنعِ القمعَينِ. أقرّبُ إجابتي لِأقربِ جزءٍ مِنْ عشرةٍ.

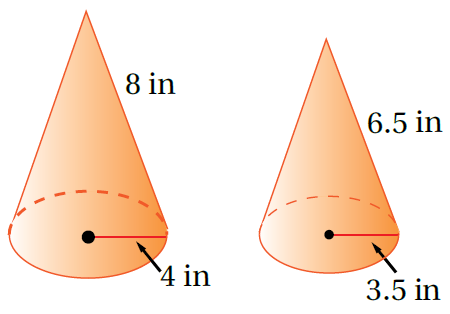
لاحظ بأن القمع سيكون مفتوح من الأسفل لذلك أجد المساحة الجانبية 

الفرقَ بينَ مساحتَيِ البلاستيكِ المستخدَمةِ في صُنعِ القمعَينِ = المساحة الجانبية للقمع الكبير - المساحة الجانبية للقمع الصغير 

$$\begin{gathered} ∆\mathrm{L}.\mathrm{A}=\mathrm{L}.{\mathrm{A}}_{\mathrm{الكبير}}-\mathrm{L}.{\mathrm{A}}_{\mathrm{الصغير} } \\ = {\mathrm{\pi r\ell }}_{\mathrm{الكبير}} -\mathrm{\pi r\ell }{ }_{\mathrm{الصغير} } \end{gathered}$$

بتعويض الأبعاد ، أجد الناتج :

$$\begin{gathered} ∆\mathrm{L}.\mathrm{A}= \mathrm{\pi }\left(4\times 8\right) -\mathrm{\pi }\left(3.5\times 6.5\right) \\ =29.1 \mathrm{in} \end{gathered}$$

 

11) وحداتُ إنارةٍ: أعودُ إلى فقرةِ(أستكشفُ)بدايةَ الدرسِ، وَأحلُّ المسألةَ.

مساحة المعدن المستخم في تصنيع الوحدة = المساحة الجانبية للمخروط 

$$\begin{gathered} \mathrm{L}.\mathrm{A}= \mathrm{\pi r\ell } \\ =\mathrm{\pi }\times 20\times 30 \\ \approx 1885 {\mathrm{cm}}^2 \end{gathered}$$

 

12) أكتشفُ الخطأَ: أوجدَ جمالٌ المساحةَ الكلّيةَ لِسطحِ  الهَرَمِ المجاورِ، وَكانَ حلُّهُ كَالآتي:

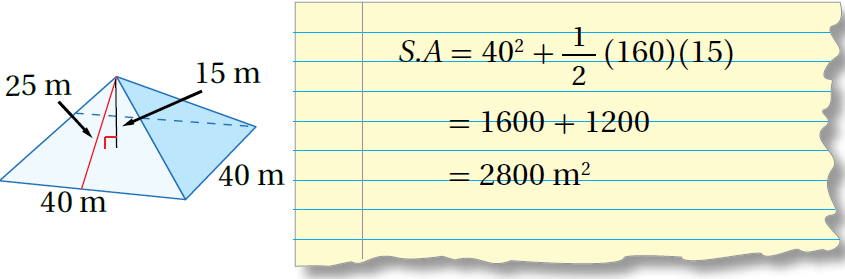
أبيّنُ الخطأَ الّذي وقعَ فيهِ جمالٌ، وَأصحّحُهُ.

الخطأ : استخدام ارتفاع الهرم 15m بدلا من 25m

التصحيح : 

 $$\begin{gathered} \mathrm{S}.\mathrm{A}=1600+\frac{1}{2}\left(160\right)\left(25\right) \\ =3600 {\mathrm{m}}^2 \end{gathered}$$

13)  تبريرٌ: أَيُّهما أطولُ؛ ارتفاعُ الهَرَمِ المنتظَمِ، أَمِ ارتفاعُهُ الجانبيُّ؟ أبرّرُ إجابتي.

الارتفاع الجانبي أطول ، لأنه يمثل الوتر في المثلث القائم الزاوية ويكون ارتفاع الهرم أحد أضلاعه 

 

14)تبريرٌ: إذا تقلّصَ نصفُ قُطرِ قاعدةِ مخروطٍ إلى النصفِ وَبقيَ الارتفاعُ نفسُهُ. ما تأثيرُ  ذلكَ في المساحةِ الجانبيةِ لِسطحِ المخروطِ؟ أبرّرُ إجابتي.

$$\begin{gathered} \mathrm{L}.{\mathrm{A}}_1=\mathrm{\pi r\ell }\underset{}{\to }\mathrm{L}.{\mathrm{A}}_2=\mathrm{\pi }\left(\frac{1}{2}{\mathrm{r}}_1\right)\mathrm{\ell } \\ \mathrm{L}.{\mathrm{A}}_2=\frac{1}{2}{\mathrm{\pi r\ell }}_1 \\ \mathrm{L}.{\mathrm{A}}_2=\frac{1}{2}\mathrm{L}.{\mathrm{A}}_1 \end{gathered}$$             تنقص المساحة إلى النصف.

 

15) أكتبُُ كيفَ أَجِدُ المساحةَ الكلّيةَ لِسطحِ المخروطِ؟

مجموع مساحته الجانبية ومساحة قاعدته 

---

---

حلول أسئلة كتاب التمارين

أَجِدُ المساحةَ الكلّيةَ لِسطحِ كلِّ مجسَّمٍ ممّا يأتي:

1)

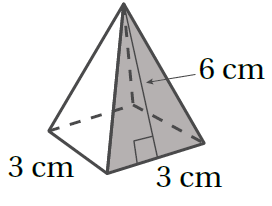
$$\begin{gathered} \mathrm{S}.\mathrm{A}=\mathrm{L}.\mathrm{A}+\mathrm{B} \\ =\left(\frac{1}{2}\mathrm{Pl}\right)+\left(\mathrm{L}\times \mathrm{W}\right) \\ =\left(\frac{\left(3\times 4\right)\times 6}{2}\right)+3^2 \\ =45 {\mathrm{cm}}^2 \end{gathered}$$              القاعدة مربعة - انتبه لتعويض المساحة والمحيط-

 

2)

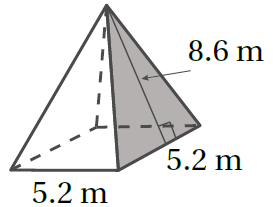
$$\begin{gathered} \mathrm{S}.\mathrm{A}=\mathrm{L}.\mathrm{A}+\mathrm{B} \\ =\left(\frac{1}{2}\mathrm{Pl}\right)+\left(\mathrm{L}\times \mathrm{W}\right) \\ =\left(\frac{\left(5.2\times 4\right)\times 8.6}{2}\right)+5.2^2 \\ =116.48 {\mathrm{m}}^2 \end{gathered}$$              القاعدة مربعة - انتبه لتعويض المساحة والمحيط-

 

3)

$$\begin{gathered} \mathrm{SA}=\mathrm{LA}+\mathrm{B} \\ =\mathrm{\pi r\ell }+{\mathrm{\pi r}}^2 \\ =\mathrm{\pi r}\left(\mathrm{\ell }+\mathrm{r}\right) \\ =3.14\times 3.2\left(5.2+3.2\right) \\ =84.4{\mathrm{mm}}^2 \end{gathered}$$

 

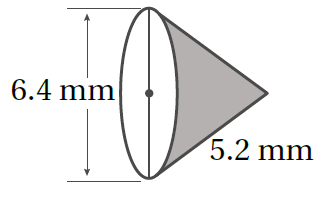
أَجِدُ المساحةَ الكلّيةَ لِسطحِ كلِّ مجسَّمٍ ممّا يأتي: 

4) منشورٌ رباعيٌّ منتظمٌ طولُ قاعدتِهِ 8cm وَارتفاعُهُ الجانِبيُّ 10cm 

$$\begin{gathered} \mathrm{S}.\mathrm{A}=\mathrm{L}.\mathrm{A}+\mathrm{B} \\ =\left(\frac{1}{2}\mathrm{Pl}\right)+\left(\mathrm{L}\times \mathrm{W}\right) \\ =\left(\frac{\left(8\times 4\right)\times 10}{2}\right)+8^2 \\ =224 {\mathrm{cm}}^2 \end{gathered}$$

 

5) مَخروطٌ ارتفاعُهُ الجانبيُّ 9dm وَطولُ نصفِ قُطرِ قاعدتِهِ 4m

$$\begin{gathered} \mathrm{SA}=\mathrm{LA}+\mathrm{B} \\ =\mathrm{\pi r\ell }+{\mathrm{\pi r}}^2 \\ =\mathrm{\pi r}\left(\mathrm{\ell }+\mathrm{r}\right) \\ =3.14\times 4\left(9+4\right) \\ =163.4 {\mathrm{dm}}^2 \end{gathered}$$

 

6) أهرامٌ: يبيّنُ الشكلُ المجاورُ أبعادَ هَرَمٍ أثريٍّ، أَجِدُ المساحةَ الجانبيةَ لَهُ. 

  

$$\begin{gathered} \mathrm{S}.\mathrm{A}=\mathrm{L}.\mathrm{A}+\mathrm{B} \\ =\left(\frac{1}{2}\mathrm{Pl}\right) \\ =\left(\frac{\left(166\times 4\right)\times 128}{2}\right) \\ =42496 {\mathrm{m}}^2 \end{gathered}$$

 

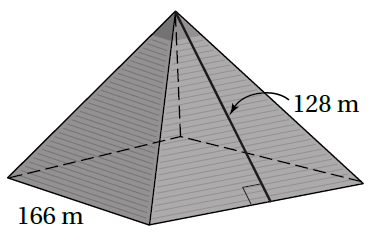
7) مَخروطٌ مساحتُهُ الجانبيةُ $\mathbf{4}\mathbf{.}\mathbf{8}\mathbf{\pi }\mathbf{ }{\mathbf{cm}}^{\mathbf{2}}$ وَطولُ نصفِ قُطْرِ قاعدتِهِ 1.2cm ، أَجِدُ الارتفاعَ الجانبيَّ لَهُ. 

$$\begin{gathered} \mathrm{LA}=\mathrm{\pi r\ell } \\ \mathrm{\ell }=\frac{\mathrm{LA}}{\mathrm{\pi r}} \\ =\frac{4.8\mathrm{\pi }}{1.2\mathrm{\pi }} \\ =4\mathrm{cm} \end{gathered}$$

 

8) أَجِدُ المساحةَ الكليةَ لِسطحِ المجسَّمِ المجاورِ.

$$\begin{gathered} \mathrm{S}.\mathrm{A}=\mathrm{L}.{\mathrm{A}}_{\mathrm{المخروط}}+\mathrm{L}.{\mathrm{A}}_{\mathrm{الأسطوانة}}+{\mathrm{A}}_{\mathrm{القاعدة} ○} \\ =\mathrm{\pi r\ell } +2\mathrm{\pi rh} +{\mathrm{\pi r}}^2 \\ =\mathrm{\pi r}\left(\mathrm{\ell }+2\mathrm{h}+\mathrm{r}\right) \\ =3.14\times 3.5\left(6.5+2\times 5+3.5\right) \\ =219.9 {\mathrm{m}}^2 \end{gathered}$$

 

9) ديكورٌ: يتكوّنُ مَنوَرُ منزلٍ مِنْ 12 قطعةَ زجاجٍ مثلثةَ الشكلِ كما في الشكلِ المجاورِ الارتفاعُ الجانبيُّ لِلمَنوَرِ  92cm وَطولُ قاعدةِ كلِّ مثلّثٍ 30cm أَجِدُ مساحةَ الزجاجِ المستخدَمةَ في تغطيةِ المَنوَرِ.

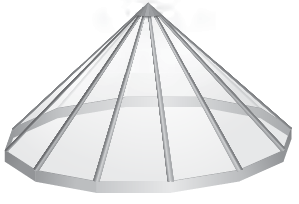
مساحة الزجاج = المساحة الجانبية 

$$\begin{gathered} \mathrm{L}.\mathrm{A}=\frac{1}{2}\mathrm{P\ell } \\ =\frac{\left(12\times 30\right)\times 92}{2} \\ =16560 {\mathrm{cm}}^2 \end{gathered}$$