حلول أسئلة أتحقق من فهمي
المساحةُ الجانبيةُ وَالمساحةُ الكلّيةُ لِسطحِ المنشورِ:
2)
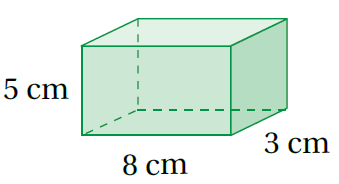
الْخُطْوَةُ 1:أَجِدُ محيطَ القاعدةِ:
P = 2l + 2w محيط القاعدة المستطيلة
P = 2(8) + 2(3) تعويض الأبعاد
22 = P أَجِدُ الناتجَ
إذنْ، محيطُ القاعدةِ 22cm
الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المنشورِ:
L.A = Ph صيغة المساحة الجانبية لسطح المنشور
22 × 5 = تعويض الأبعاد
110 = أَجِدُ الناتجَ
إذنْ، المساحةُ الجانبيةُ لِسطحِ المنشورِ 110cm2
الْخُطْوَةُ 3: أَجِدُ مساحةَ القاعدةِ:
B = l × w مساحة القاعدة
3 × 8 = تعويض الأبعاد
24 = أَجِدُ الناتجَ
إذنْ، مساحةُ قاعدةِ المنشورِ 24cm2
الْخُطْوَةُ 4:أَجِدُ المساحةَ الكلّيةَ لِسطحِ المنشورِ:
S.A = L.A + 2B صيغة المساحة الكلية لسطح المنشور
(24)110+2= تعويض الأبعاد
158 = أَجِدُ الناتجَ
إذنْ، المساحةُ الكلّيةُ لِسطحِ المنشورِ تساوي 158cm2
3)
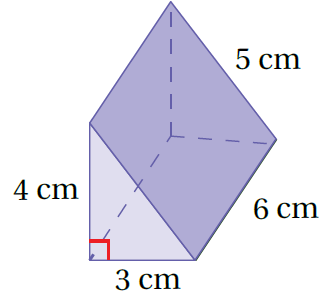
الْخُطْوَةُ 1:أَجِدُ محيطَ القاعدةِ:
P = l+w+h محيط القاعدة (مثلث)
P = 5+3+4 تعويض الابعاد
12 = أَجِدُ الناتجَ
إذنْ، محيطُ القاعدةِ 12cm
الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المنشورِ:
L.A = Ph صيغة المساحة الجانبية لسطح المنشور
6 × 12 = تعويض الابعاد
72 = أَجِدُ الناتجَ
إذنْ، المساحةُ الجانبيةُ لِسطحِ المنشورِ 72cm2
الْخُطْوَةُ 3: أَجِدُ مساحةَ القاعدةِ:
= B مساحة القاعدة (مثلث)
= تعويض الابعاد
6 = أَجِدُ الناتجَ
إذنْ، مساحةُ قاعدةِ المنشورِ 6cm2
الْخُطْوَةُ 4:أَجِدُ المساحةَ الكلّيةَ لِسطحِ المنشورِ:
S.A = L.A + 2B صيغة المساحة الكلية لسطح المنشور
(6)72+2 = تعويض الابعاد
84 = أَجِدُ الناتجَ
إذنْ، المساحةُ الكلّيةُ لِسطحِ المنشورِ تساوي 84cm2
من مثال 2: أَجِدُ المساحةَ الكلّيةَ لِسطحِ المبنى إذا علمْتُ أنَّ مساحةَ قاعدتِهِ 39200m2
S.A = L.A + 2B صيغة المساحة الكلية لسطح المنشور
تعويض الأبعاد
103820 = أَجِدُ الناتجَ
إذنْ، المساحةُ الكلّيةُ لِسطحِ المبنى تساوي 103820cm2
المساحةُ الجانبيةُ وَالمساحةُ الكلّيةُ لِسطحِ الأسطوانة :
2)
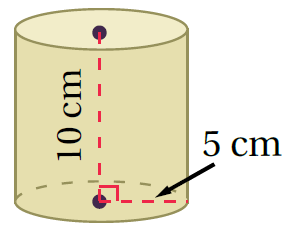
المساحة الجانبية :
صيغة المساحة الجانبية لسطح الأسطوانة
بتعويض الأبعاد أجد الناتج
المساحة الكلية:
صيغة المساحة الكلية لسطح الأسطوانة
إذنْ، المساحةُ الجانبيةُ لِسطحِ الأُسطوانةِ تساوي 314.16cm2 تقريبًا، وَالمساحةُ الكلّيةُ لَهُ تساوي 471.24cm2 تقريبًا
3)
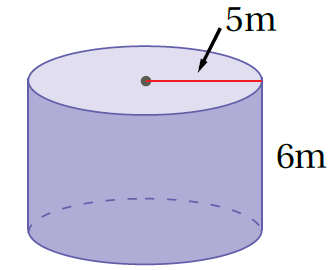
المساحة الجانبية :
صيغة المساحة الجانبية لسطح الأسطوانة
بتعويض الأبعاد ، أجد الناتج
المساحة الكلية:
صيغة المساحة الكلية لسطح الأسطوانة
إذنْ، المساحةُ الجانبيةُ لِسطحِ الأُسطوانةِ تساوي 188.5m2 تقريبًا، وَالمساحةُ الكلّيةُ لَهُ تساوي 345.58m2 تقريبًا
علبٌ: يُنتجُ مصنعٌ علبًا أُسطوانيةَ الشكلِ، ارتفاعُ الواحدةِ منها 7cm وَطولُ قُطرِها 5cm أَجِدُ المساحةَ الكلّيةَ لِسطحِ العُلبةِ أقرّبُ إجابتي لِقربِ جزءٍ مِنْ عشرةٍ.
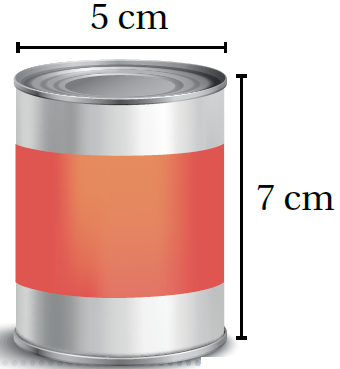
صيغة المساحة الكلية لسطح الأسطوانة - بأخذ عامل مشترك-
بتعويض الأبعاد ، أجد الناتج
حلول أسئلة أتدرب وأحل المسائل
أَجِدُ المساحةَ الجانبيةَ لِسطحِ كلِّ مجسَّمٍ ممّا يأتي:
1)
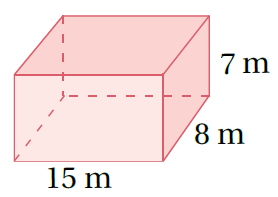
L.A = Ph صيغة المساحة الجانبية لسطح المنشور
L.A = (2l+2w)h تعويض محيط المستطيل P
بتعويض الأبعاد ، أجد الناتج
2)
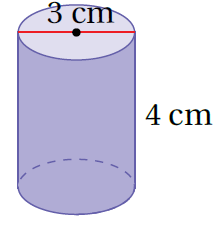
صيغة المساحة الجانبية لسطح الأسطوانة
بتعويض الأبعاد ، أجد الناتج
3)
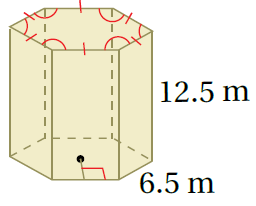
L.A = Ph صيغة المساحة الجانبية لسطح المنشور
تعويض محيط القاعدة السداسية
بتعويض الأبعاد ، أجد الناتج
أَجِدُ المساحةَ الكلية لِسطحِ كلِّ مجسَّمٍ ممّا يأتي:
4)
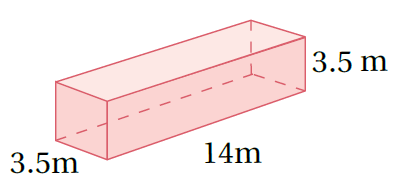
الْخُطْوَةُ 1:أَجِدُ محيطَ القاعدةِ:
P = 2l + 2w محيط القاعدة المستطيلة
P = 2(14) + 2(3.5) تعويض الأبعاد
35 = P أَجِدُ الناتجَ
الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المنشورِ:
L.A = Ph صيغة المساحة الجانبية لسطح المنشور
3.5×35 = تعويض الأبعاد
122.5 = أَجِدُ الناتجَ
الْخُطْوَةُ 3: أَجِدُ مساحةَ القاعدةِ:
B = l × w مساحة القاعدة
3.5 ×14 = تعويض الأبعاد
49 = أَجِدُ الناتجَ
الْخُطْوَةُ 4:أَجِدُ المساحةَ الكلّيةَ لِسطحِ المنشورِ:
S.A = L.A + 2B صيغة المساحة الكلية لسطح المنشور
(49)122.5+2 = تعويض الأبعاد
220.5 = أَجِدُ الناتجَ
إذنْ، المساحةُ الكلّيةُ لِسطحِ المنشورِ تساوي 220.5cm2
5)
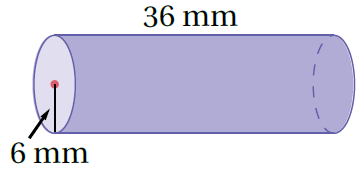
صيغة المساحة الكلية لسطح الأسطوانة - بأخذ كعامل مشترك -
بتعويض الأبعاد ، أجد الناتج
6)
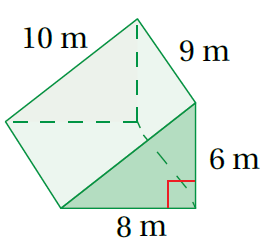
الْخُطْوَةُ 1:أَجِدُ محيطَ القاعدةِ:
P = l+w+h محيط القاعدة (مثلث)
P = 6+10+8 تعويض الابعاد
24 = أَجِدُ الناتجَ
الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المنشورِ:
L.A = Ph صيغة المساحة الجانبية لسطح المنشور
9 × 24 = تعويض الابعاد
216 = أَجِدُ الناتجَ
الْخُطْوَةُ 3: أَجِدُ مساحةَ القاعدةِ:
=B مساحة القاعدة (مثلث)
بتعويض الأبعاد ، أجد الناتج
الْخُطْوَةُ 4:أَجِدُ المساحةَ الكلّيةَ لِسطحِ المنشورِ:
S.A = L.A + 2B صيغة المساحة الكلية لسطح المنشور
(24)216+2 = تعويض الابعاد
264 = أَجِدُ الناتجَ
إذنْ، المساحةُ الكلّيةُ لِسطحِ المنشورِ تساوي 264m2
أَجِدُ المساحةَ الكلية لِسطحِ كلِّ مجسَّمٍ ممّا يأتي:
7) منشورٌ قاعدتُهُ مستطيلةُ الشكلِ، طولُها 6.2cm وَعرضُها 4cm وَارتفاعُهُ 8.5cm
الْخُطْوَةُ 1:أَجِدُ محيطَ القاعدةِ:
P = 2l + 2w محيط القاعدة المستطيلة
P = 2(6.2) + 2(4) تعويض الأبعاد
20.4 = P أَجِدُ الناتجَ
الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المنشورِ:
L.A = Ph صيغة المساحة الجانبية لسطح المنشور
8.5×20.4 = تعويض الأبعاد
173.4 = أَجِدُ الناتجَ
الْخُطْوَةُ 3: أَجِدُ مساحةَ القاعدةِ:
B = l × w مساحة القاعدة
4 × 6.2 = تعويض الأبعاد
24.8 = أَجِدُ الناتجَ
الْخُطْوَةُ 4:أَجِدُ المساحةَ الكلّيةَ لِسطحِ المنشورِ:
S.A = L.A + 2B صيغة المساحة الكلية لسطح المنشور
(24.8)173.4+2 = تعويض الأبعاد
223 = أَجِدُ الناتجَ
إذنْ، المساحةُ الكلّيةُ لِسطحِ المنشورِ تساوي 223cm2
8)أُسطوانةٌ طولُ نصفِ قُطرِها 5mm وَارتفاعُهُا 15mm
صيغة المساحة الكلية لسطح الأسطوانة - بأخذ كعامل مشترك-
بتعويض الأبعاد ، أجد الناتج
9) أُسطوانةٌ طولُ قُطرِها 4m وَارتفاعُها 20m
صيغة المساحة الكلية لسطح الأسطوانة - بأخذ كعامل مشترك-
بتعويض الأبعاد ، أجد الناتج
10) أقلامٌ: قلمُ تلوينٍ على شكلِ منشورٍ سُداسيٍّ، طولُ ضِلعِ قاعدتِهِ 4mm وَارتفاعُهُ 170mm أَجِدُ المساحةَ الجانبيةَ للقلم
L.A = Ph صيغة المساحة الجانبية لسطح المنشور
تعويض محيط القاعدة السداسية
بتعويض الأبعاد ، أجد الناتج
11) ناطحاتُ سحابٍ: ناطحةُ سحابٍ على شكلِ منشورٍ قاعدتُهُ مربعةُ الشكلِ طولُ ضِلعِها 64m وَارتفاعُهُ 414m أَجِدُ المساحةَ الجانبيةَ لِسطحِ ناطحةِ السحابِ.
L.A = Ph صيغة المساحة الجانبية لسطح المنشور
بتعويض محيط القاعدة المربعة = 4× طول الضلع
بتعويض الأبعاد ، أجد الناتج
12) أبراجٌ: يبلغُ ارتفاعُ بُرجِ الساعةِ في مكّةَ المكرَّمةِ 250m وَهُوَ على شكلِ منشورٍ قاعدتُهُ مربعةُ الشكلِ طولُ ضِلعِها 43m أَجِدُ المساحةَ الجانبيةَ لِسطحِ البُرجِ.
L.A = Ph صيغة المساحة الجانبية لسطح المنشور
بتعويض محيط القاعدة المربعة = 4× طول الضلع
بتعويض الأبعاد ، أجد الناتج
13) أَجِدُ مساحةَ الكرتونِ اللازمةَ لِصُنعِ الأنبوبِ الآتي:
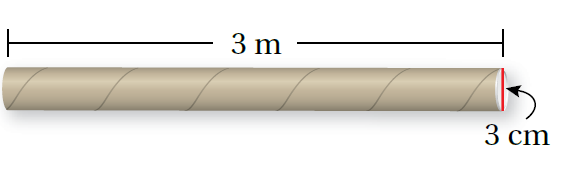
مساحة الكرتون اللازمة لصنع الأنبوب = المساحة الجانبية للأنبوب - أنتبه لتحويل الوحدات قبل الحل -
صيغة المساحة الجانبية لسطح الأسطوانة
بتعويض الأبعاد ، أجد الناتج
14) عُلَبٌ: غَلّفَتْ منارُ جوانبَ عُلبةِ الأقلامِ المجاورةِ وَقاعدتَها بِورقٍ للتزيينِ. أَجِدُ مساحةَ ورقِ التغليفِ الّذي استعملَتْهُ منارُ.
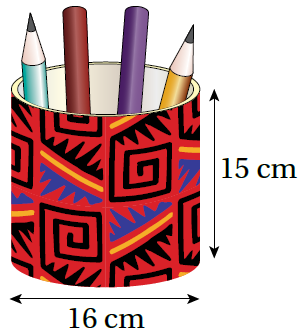
مساحة ورق التغليف = المساحة الكلية للأسطوانة - مساحة الغطاء العلوي
صيغة المساحة الكلية لسطح الأسطوانة - مساحة الغطاء العلوي (لاحظ تعويض B وليس 2B)
بتعويض الأبعاد ، أجد الناتج
15) بيوتٌ زجاجيةٌ: يبيّنُ الشكلُ المجاورُ بيتًا زجاجيًّا لِلنباتاتِ، أَجِدُ مساحةَ الزجاجِ الّتي استُعمِلَتْ في بناءِ البيتِ.
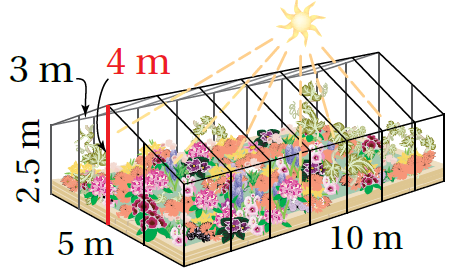
مساحة الزجاج = المساحة الكلية للمنشور الخماسي - مساحة الأرض السفلية
أجد محيط الشكل الخماسي :
محيط المنشور يساوي مجموع أطوال أضلاعه
أجد مساحة الشكل الخماسي :
مساحة الشكل الخماسي = مساحة المستطيل + مساحة المثلث (ارتفاع المثلث = 2.5-4)
أجد مساحة الزجاج :
صيغة المساحة الكلية لسطح المنشور - مساحة الأرض السفلية
16) راصفةُ طُرُقٍ: أعودُ إلى فقرةِ (أستكشفُ) بِدايةَ الدرسِ، وَأحلُّ المسألةَ.
المساحة المرصوفة من الطريق = مساحة الأسطوانة الجانبية
صيغة المساحة الجانبية لسطح الأسطوانة
تحدٍّ: أَجِدُ المساحةَ الكلّيةَ لِسطحِ كلِّ مجسَّمٍ ممّا يأتي:
17)
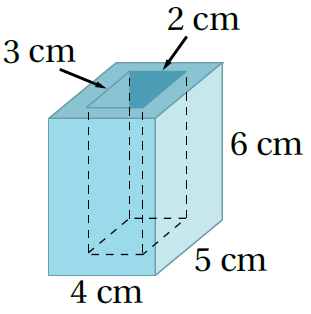
الْخُطْوَةُ1: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المنشورِ:
L.A = Ph صيغة المساحة الجانبية لسطح المنشور
بتعويض محيط المستطيل وارتفاع المنشور ، أجد الناتج
الْخُطْوَةُ 2: أَجِدُ مساحةَ القاعدةِ:
مساحة القاعدة
بتعويض أبعاد المستطيلين ، أجد الناتج
الْخُطْوَةُ 3:أَجِدُ المساحةَ الكلّيةَ لِسطحِ المنشورِ:
S.A = L.A + 2B صيغة المساحة الكلية لسطح المنشور
(14)108+2= تعويض الأبعاد
136 = أَجِدُ الناتجَ
إذنْ، المساحةُ الكلّيةُ لِسطحِ المنشورِ تساوي 136cm2
18)
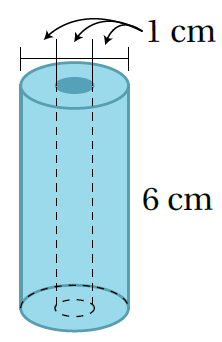
الْخُطْوَةُ1: أَجِدُ المساحةَ الجانبيةَ لِسطحِ الأسطوانة :
صيغة المساحة الجانبية لسطح الأسطوانة
بتعويض الأبعاد ، أجد الناتج
الْخُطْوَةُ 2: أَجِدُ مساحةَ القاعدةِ:
مساحة القاعدة
بتعويض الأبعاد ، أجد الناتج
الْخُطْوَةُ 3:أَجِدُ المساحةَ الكلّيةَ لِسطحِ الأسطوانة:
S.A = L.A + 2B صيغة المساحة الكلية لسطح الأسطوانة
(6.3)56.5+2 تعويض الأبعاد
أَجِدُ الناتجَ
إذنْ، المساحةُ الكلّيةُ لِسطحِ المنشورِ تساوي 69.1cm2
19) تبريرٌ: إذا أصبحَتْ أطوالُ أضلاعِ مكعَّبٍ مِثْلَيْ طولِها الأصليِّ، فَما تأثيرُ ذلكَ في المساحةِ الكلّيةِ لِسطحِهِ؟ أبرّرُ إجابتي.
المساحة الجديدة 4 أمثال المساحة الأصلية.
20) أكتشفُ الخطأَ: يقولُ سيفٌ: إذا تساوى حجما أُسطوانتَينِ، فإنَّهُ يكون لَهُما المساحةُ الجانبيةُ نفسُها. هلْ ما يقولُهُ سيفٌ صحيحٌ؟ أبرّرُ إجابتي.
غير صحيح ، لأن تساوي الحجمين لا يعني تساوي أبعاد الأسطوانتين ، فمن الممكن أن يتساوى حجما الأسطوانيتين مع اختلافهما في القطر والارتفاع مما يعني اختلاف مساحتهما الجانبية
21) تحدٍّ: يبيّنُ الشكلُ المجاورُ 4 كراتِ تِنسٍ موضوعةً في عُلبةٍ أُسطوانيةِ الشكلِ. إذا كانَ قُطرُ كلِّ كرةٍ مِنْها 7cm فَأَجِدُ المساحَةَ الجانبيةَ لِسطحِ العُلبةِ، وَأبرّرُ إجابتي.

المساحةَ الجانبيةَ لِسطحِ الأسطوانة :
ارتفاع الأسطوانة = 4 × قطر الكرة الواحدة و قطر الأسطوانة = قطر الكرة تقريباً
22) أكتبُُ كيفَ أَجِدُ المساحةَ الجانبيةَ وَالمساحةَ الكلّيةَ لِسطحِ المنشورِ؟
المساحةَ الجانبيةَ: ناتج ضرب ارتفاع المنشور في محيط قاعدته
المساحةَ الكلّيةَ : مجموع مساحته الجانبية ومثلي مساحة قاعدته
حلول أسئلة كتاب التمارين
أَجِدُ المساحةَ الكليةَ لسطحِ كلِّ مجسَّمٍ ممّا يأتي:
1)
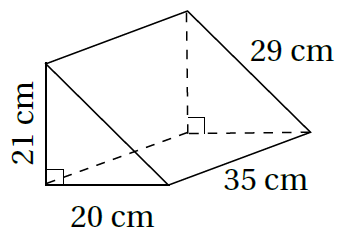
2)
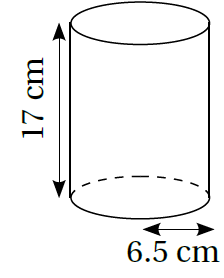
3)
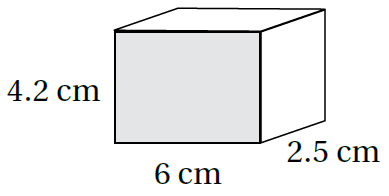
أَجِدُ المساحةَ الكلّيةَ لِسطحِ كلِّ مجسَّمٍ ممّا يأتي:
4) أُسطُوانةٌ ارتفاعُها 9.4m ، وَطولُ قُطرِ قاعدتِها 8m
5) منشورٌ رباعيٌّ قاعدتُهُ مستطيلةُ الشكلِ طولُهُا 3cm وعَرضُهُا 5cm وَارتفاعُهُ 4cm
6) يبيّنُ الشكلُ المجاورُ منشورًا خماسيًّا قاعدتُهُ منتظمةٌ مساحتُها 43cm2 طولُ ضلعِها 5cm .إذا كانَتِ المساحةُ الكليةُ لسطحِ المنشورِ 236cm2، فَأَجِدُ قيمةَ a
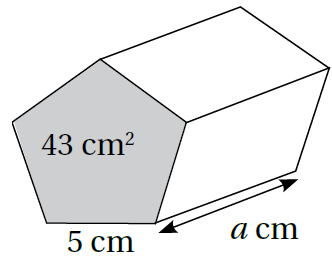
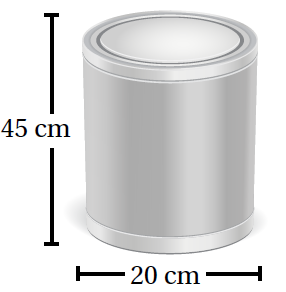
7) عبوّةُ طلاءٍ: يبيّنُ الشكلُ المجاورُ عبوّةَ طلاءٍ على شكلِ أُسطُوانةٍ.أَجِدُ المساحةَ الكليةَ لسطحِ العبوّةِ.
8) منشورٌ ثلاثيٌّ، أبعادُ قاعدتِهِ 4cm,5cm,6cm وَمساحتُهُ الجانبيةُ 300cm2، أَجِدُ ارتفاعَهُ.
9) أكتشفُ الخطأَ: أوجدَ عاصمٌ المساحةَ الكليةَ لسطحِ الأُسطُوانةِ المجاورةِ كما يأتي: أحدّدُ الخطأَ الّذي وقعَ فيهِ عاصمٌ، ثمَّ أصحّحُهُ.
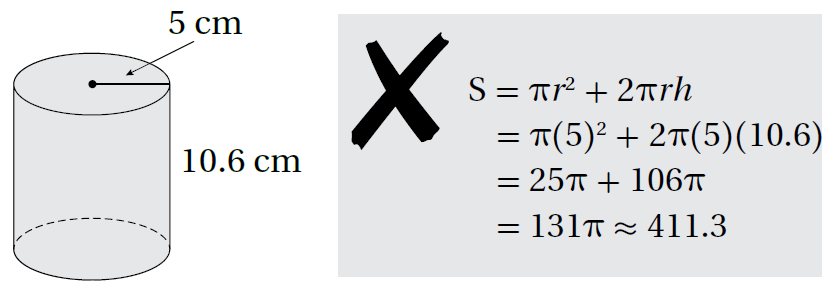
الخطأ أنه حسب مساحة قاعدة واحدة، عند حساب مساحة القاعدتين تكون الإجابة الصحيحة 490cm2 تقريبا