رياضيات أدبي فصل أول

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 37

أجد باستعمال كلٍّ من الطرائق الآتية عدد الطرائق المُمكِنة لتكوين رقم سري من منزلتين باستعمال الأرقام: 3 , 5 , 7 , 9، علمًا بأنَّه يجوز تكرار الرقم في المنزلتين:

a) المُخطَّط الشجري.
b) الجدول.
c) القائمة المنظمة.

الحل : 

a) المُخطَّط الشجري. 

 

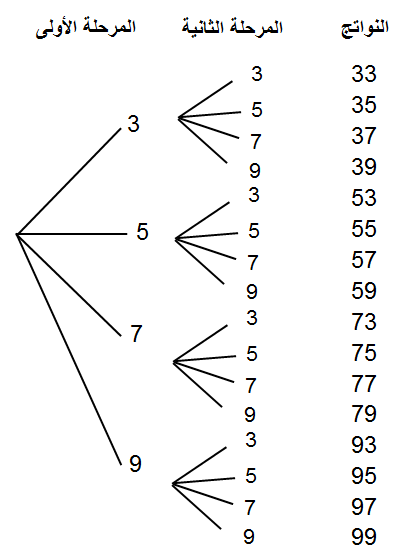
عدد النواتج  = 16 

---

b) الجدول.

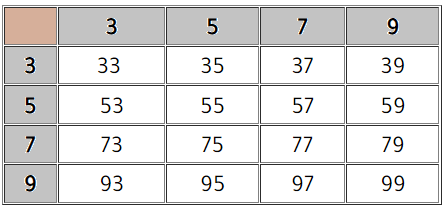
عدد النواتج  = 16 

---

c) القائمة المنظمة.

عدد النواتج  = 16 

---

 

أتحقق من فهمي صفحة 38

طعام : بكم طريقة مختلفة يُمكِن لشخص اختيار وجبة غدائه المُكوَّنة من طبق رئيس واحد، وطبق مقبلات واحد، وطبق حساء واحد، من قائمة وجبة اليوم التي يُقدِّمها أحد المطاعم؟ الحل :  باستخدام مبدأ العد الأساسي  :        عدد طرائق اختيار طبق مقبلات             عدد طرائق اختيار طبق حساء           عدد طرائق اختيار طبق رئيس                                       5                         $\times$                           4                           $\times$                       3  إذن توجد 60 طريقة مختلفة لاختيار الوجبة .

   

 

 

 

 

 

 

 

 

---

 

أتحقق من فهمي صفحة 40

أجد في كلٍّ من الحالات الآتية عدد الطرائق المُمكِنة لتكوين رقم مركبة مُكوَّن من 5 منازل ، مُستعمِلًا الأرقام : 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 :

a) إذا سُمِح بالتكرار.
b) إذا لم يُسمح بالتكرار.
c) إذا سُمِح بالتكرار ؛ شرط وضع الرقم 9 في أول منزلة من اليسار.

الحل : 

a) إذا سُمِح بالتكرار.    

 $9 \times 9 \times 9 \times 9 \times 9 = 59049$

b) إذا لم يُسمح بالتكرار. 

 $9 \times 8 \times 7 \times 6 \times 5 = 15120$

c) إذا سُمِح بالتكرار ؛ شرط وضع الرقم 9 في أول منزلة من اليسار.

 $1 \times 9 \times 9 \times 9 \times 9 = 6561$

---

 

أسئلة أتدرب وأحل المسائل

شراء : ترغب حنين في شراء هاتف محمول، فذهبت إلى أحد محالِّ بيع الهواتف ، ووجدت فيه 4 أنواع مختلفة من الهواتف: H , I , S , N ، لكل نوع منها ثلاثة ألوان : أحمر : R ، وأسود : B ، وأبيض :  W
أجد عدد الطرائق المُمكِنة لشراء حنين هاتفًا محمولًا باستعمال : 

1 المُخطَّط الشجري.                                   2 الجدول.                                                    3 القائمة المنظمة.

الحل : 

1 المُخطَّط الشجري. 

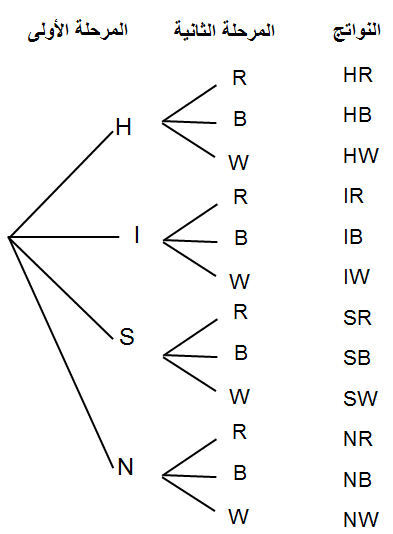
عدد النواتج  = 12 

 

---

 2 الجدول.   

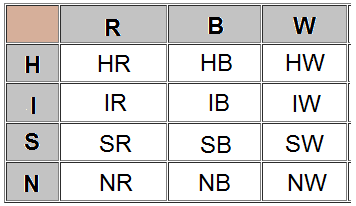
عدد النواتج  = 12 

---

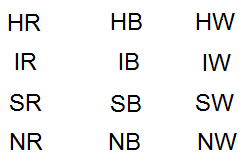
عدد النواتج  = 12 

---

4) طعام : يُعِدُّ مطعمٌ البيتزا باستعمال نوعين من العجين ، و 8 خلطات مختلفة. إذا كان لهذه البيتزا 3 حجوم ، فكم عدد الخيارات المُمكِنة لشراء بيتزا واحدة منها؟

الحل : 

باستخدام مبدأ العد الأساسي  : 

      عدد طرائق اختيار الحجم             عدد طرائق اختيار نوع الخلطة          عدد طرائق اختيار نوع العجين

                                                                                        2                        $\times$                           8                             $\times$                         3

إذن : عدد الخيارات المُمكِنة لشراء بيتزا واحدة = 48    

---

 

5) يشترط موقع تعليمي في شبكة الإنترنت إنشاء المُستخدِم حسابًا محميًّا بكلمة مرور تحوي 4 أحرف إنجليزية (من دون اهتمام بحجم الخط) متبوعة بعدد مُكوَّن من رقم واحد. ما عدد كلمات المرور المختلفة التي يُمكِن إنشاؤها؟

الحل : 

عدد أحرف اللغة الانجليزية  =  26    ،   عدد الأرقام = 10 

باستخدام مبدأ العد الأساسي  :  $26 \times 26 \times 26 \times 26 \times 10 = 4569760$

---

 

كرات : يحتوي صندوق على كرة حمراء، وكرة خضراء، وكرة بيضاء. أجد عدد الطرائق المُمكِنة لسحب كرتين على التوالي في الحالتين الآتيتين:

6) إذا سُمِح بإعادة الكرة المسحوبة الأولى.

7) إذا لم يُسمَح بإعادة الكرة المسحوبة الأولى.

الحل : 

6) باستخدام مبدأ العد الأساسي  :  $3 \times 3 = 9$

7) باستخدام مبدأ العد الأساسي  :   $3 \times 2 = 6$

---

 

8) مختبر: تريد شيماء اختيار زميلتين لتكوين مجموعة ثلاثية تُنفِّذ تجربة في مختبر العلوم. بكم طريقة مختلفة يُمكِنها تكوين مجموعتها، علمًا بأنَّ عدد طالبات الصف 21 طالبة؟

الحل : 

باستخدام مبدأ العد الأساسي  :

            عدد طرائق اختيار الزميلة الثانية          عدد طرائق اختيار الزميلة الأولى   

                                                                                                                                                                     21                   $\times$                      20

يوجد  420 طريقة أمام شيماء لتكوين مجموعتها . 

---

 

9) لدى حاتم ثلاثة قمصان مختلفة الألوان ، وبنطالان مختلفا اللون. أجد عدد الطرائق المُمكِنة لاختيار حاتم قميصًا وبنطالًا؟

الحل : 

باستخدام مبدأ العد الأساسي  : 

                       عدد طرائق اختيار البنطال          عدد طرائق اختيار القميص   

                                                                                                                                                  3             $\times$                     2    

يوجد  6 طرق أمام حاتم للاختيار . 

---

 

10) أحُلُّ المسألة الواردة في بند (مسألة اليوم).

مسألة اليوم :  بكم طريقة يُمكِن لرولا اختيار قطعة شوكولاتة من بين 3 أنواع، وقطعة بسكويت من بين 6 أنواع؟

الحل : 

  عدد طرائق اختيار البسكويت          عدد طرائق اختيار  الشوكولاتة

                                                                                                                                  3                        $\times$                     6

يوجد  18 طريقة أمام رولا للاختيار . 

---

 

11) تحدٍّ: يستطيع بشير استعمال 480 طريقة مختلفة لاختيار وجبة غدائه من بين المقبلات، والطبق الرئيس، والحلويات. إذا كان للمقبلات 6 خيارات، وللطبق الرئيس 10 خيارات، فما عدد الخيارات المُمكِنة للحلويات، علمًا بأنَّه اختار طبقًا واحدًا من كل صنف؟

الحل : 

أفرض عدد الخيارات الممكنة للحلويات  = y 

باستخدام مبدأ العد الأساسي  :

 $$\begin{gathered} 10 \times 6 \times y = 480 \\ 60 y = 480 \\ y = \frac{480}{60} = 8 \end{gathered}$$

عدد الخيارات الممكنة للحلويات = 8

---

12)  تبرير: كم عددًا من 4 منازل يقبل القسمة على 5 ، ويُمكِن تكوينه باستعمال الأرقام : 1 , 2 , 3 , 4 , 5، إذا سُمِح بالتكرار ، مُبرِّرًا إجابتي؟

الحل : 

العدد الذي يقبل القسمة على  5 يجب أن يكون آحاده الرقم  5 ، إذن لمنزلة الآحاد طريقة واحدة فقط للاختيار ، وباقي المنازل لكل منها 5 طرق للسماح بالتكرار .

 عدد طرائق اختيار منزلة الآحاد         عدد طرائق اختيار منزلة العشرات             عدد طرائق اختيار منزلة المئات           عدد طرائق اختيار الألوف

                                5             $\times$                             5                        $\times$                               5                            $\times$                       1

إذن عدد الطرق  = 125 طريقة .

---

13) تحدٍّ: كم عددًا فرديًّا من 3 منازل يُمكِن تكوينه باستعمال الأرقام ( 0 - 9)، علمًا بأنَّه لا يُسمَح بالتكرار؟

الحل : 

 عدد طرائق اختيار منزلة الآحاد         عدد طرائق اختيار منزلة العشرات             عدد طرائق اختيار منزلة المئات 

                                                                                                                                                 9                        $\times$                              10                      $\times$                        5

إذن عدد الطرق  = 450 طريقة .

---

14) أكتب: كيف يستفاد من مبدأ العَدِّ الأساسي في إيجاد عدد الطرائق المختلفة لإجراء تجربة عشوائية مُتعدّدة المراحل؟

الاجابة : بضرب عدد الطرق الممكنة في كل مرحلة بعضها في بعض . 

---

 

 

أسئلة كتاب التمارين

أجد عدد الطرائق المُمكِنة لظهور شخص بزي مُكوَّن من بنطال يتوافر منه 3 ألوان (أسود، وأزرق، وبني)، و 3 قمصان يتوافر
منها 3 ألوان (أبيض، وأخضر، ورمادي)، مُستعمِلًا :
1 الرسم الشجري.
2 الجدول.
3 القائمة المنظمة.

الحل :

1 الرسم الشجري.

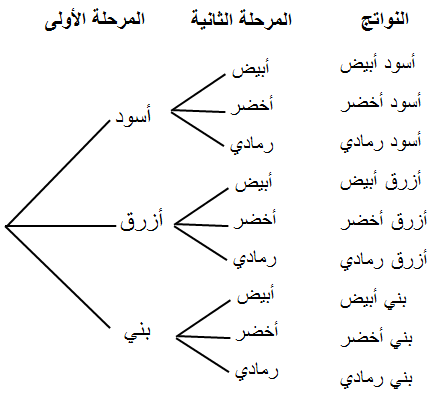
2 الجدول.

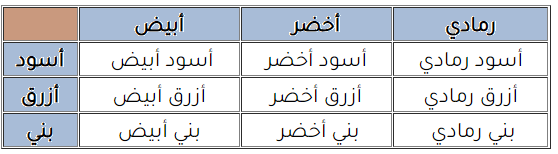
3 القائمة المنظمة.

---

 

4) في محل لبيع القرطاسية 8 أنواع مختلفة من الأقلام ، و 6 أنواع مختلفة من الدفاتر المدرسية. أجد عدد الطرائق المُمكِنة لاختيار قلم واحد ودفتر واحد.
الحل :

باستخدام مبدأ العد الأساسي  : $8 \times 6 = 48$

 

---

بكم طريقة يُمكِن اختيار نوعين من الحلويات من بين 7 أنواع مختلفة ، ونوعين من المشروبات الساخنة من بين 5 أنواع مختلفة :

5) إذا سُمِح بالتكرار؟
6) إذا لم يُسمَح بالتكرار؟
7) إذا سُمِح بتكرار أنواع الحلويات فقط؟

الحل :

5) إذا سُمِح بالتكرار؟

$7\times 7 \times 5 \times 5 = 1225$

6) إذا لم يُسمَح بالتكرار؟

$7\times 6 \times 5 \times 4 = 840$

7) إذا سُمِح بتكرار أنواع الحلويات فقط؟

$7\times 7 \times 5 \times 4 = 980$

---

أجد عدد الطرائق المُمكِنة لتكوين رمز دخول للبريد الإلكتروني، يتألَّف من حرفين من حروف الإنجليزية (عددها 26 حرفًا) من دون الاهتمام بحجم الحرف، ورقمين من الأرقام : 9 , 8 , 7 , 6 , 5 , 4 , 3 , 2 , 1 :

8) إذا سُمِح بالتكرار.
9) إذا لم يُسمَح بالتكرار.
10) إذا كان الحرف الأول B، ولا يُسمَح بالتكرار.

الحل :

8) إذا سُمِح بالتكرار.

$26\times 26 \times 9 \times 9 = 54756$

9) إذا لم يُسمَح بالتكرار.

$26\times 25 \times 9 \times 8 = 46800$

10) إذا كان الحرف الأول B، ولا يُسمَح بالتكرار.

$1\times 25 \times 9 \times 8 =1800$

---

11) جامعات : ترغب فاطمة في اختيار تخصُّص من بين سبعة تخصُّصات جامعية ، وكذلك اختيار جامعة من بين أربع جامعات قريبة من منزلها. بكم طريقة يُمكِنها اختيار التخصُّص والجامعة؟

الحل :

$7 \times 4 = 28$

---