رياضيات فصل أول

حلول أسئلة أتحقق من فهمي 

3) $\mathbf{m}\mathbf{\angle }\mathbf{5}$

$$\begin{gathered} \mathrm{m}\angle 5=180°-\left(\mathrm{m}\angle 2+25°\right) \\ =180°-\left(125°+25°\right) \\ =30° \end{gathered}$$                                         مجموع زوايا المثلث الداخلية

4) $\mathbf{m}\mathbf{\angle }\mathbf{3}$

$$\begin{gathered} \mathrm{m}\angle 3+\mathrm{m}\angle 2=180° \\ =180°-125° \\ =55° \end{gathered}$$                                                    زاويتان متجاورتان على مستقيمٍ 

5)$\mathbf{m}\mathbf{\angle }\mathbf{1}$

$$\begin{gathered} \mathrm{m}\angle 1=180°-\left(\mathrm{m}\angle 3+60°\right) \\ =180°-\left(55°+60°\right) \\ =65° \end{gathered}$$                                        مجموع زوايا المثلث الداخلية

 

3) $\mathbf{m}\mathbf{\angle }\mathbf{3}$

$$\begin{gathered} \mathrm{m}\angle 3=\mathrm{m}\angle 1+60° \\ =70°+60° \\ =130° \end{gathered}$$                                                      زاويةٌ خارجيةٌ للمثلثِ

4) $\mathbf{m}\mathbf{\angle }\mathbf{4}$

$\mathrm{m}\angle 4=110°$                                                                بالتناظر 

5) $\mathbf{m}\mathbf{\angle }\mathbf{5}$

$$\begin{gathered} \mathrm{m}\angle 5=\mathrm{m}\angle 2 \\ =50° \end{gathered}$$                                                               بالتناظر 

---

---

حلول أسئلة أتدرب وأحل المسائل 

أجدُ قياساتِ الزوايا المرقَّمةِ في كلٍّ منَ الأشكالِ الآتيةِ:

1)

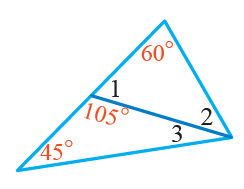
قياس الزاوية 1:

$$\begin{gathered} \mathrm{m}\angle 1=180°-105° \\ =75° \end{gathered}$$                                                     زاويتان متجاورتان على مستقيمٍ 

قياس الزاوية 2:

$$\begin{gathered} \mathrm{m}\angle 2=180°-\left(75°+60°\right) \\ =45° \end{gathered}$$                                           مجموع زوايا المثلث الداخلية

قياس الزاوية 3:

$$\begin{gathered} \mathrm{m}\angle 3=180°-\left(105°+45°\right) \\ =30° \end{gathered}$$                                         مجموع زوايا المثلث الداخلية

2)

$$\begin{gathered} =180°-\left(70+47\right)° \\ =63° \end{gathered}$$                                                      مجموع زوايا المثلث الصغير الداخلية

قياس الزاوية 1 : 

$$\begin{gathered} \mathrm{m}\angle 1=180°-\left(63+32\right)° \\ =85° \end{gathered}$$                                             قياس الزاوية الثالثة في المثلث الأكبر  °63 بالتقابل بالرأس ، ومجموع زوايا المثلث الداخلية 180 درجة

3)

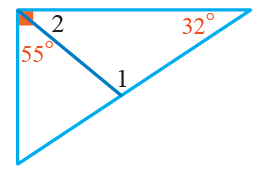
قياس الزاوية 2: 

$$\begin{gathered} \mathrm{m}\angle 2=90°-55° \\ =35° \end{gathered}$$                                                         مجموع قياس الزاويتيين 90 درجة 

قياس الزاوية1: 1

$$\begin{gathered} \mathrm{m}\angle 1=180°-\left(35+32\right)° \\ =113° \end{gathered}$$                                              مجموع زوايا المثلث الداخلية

4)

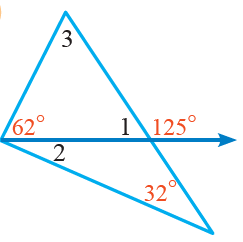
قياس الزاوية 1:

$$\begin{gathered} \mathrm{m}\angle 1=180°-125° \\ =55° \end{gathered}$$                                                     زاويتان متجاورتان على مستقيمٍ 

قياس الزاوية 2:

$$\begin{gathered} \mathrm{m}\angle 2=\mathrm{m}\angle 1-32° \\ =55°-32° \\ =23° \end{gathered}$$                                                      الزاوية 1 ، زاوية خارجية للمثلث السفلي ، ويساوي مجموع قياس الزاويتيين البعيدتين 

قياس الزاوية 3:

$$\begin{gathered} \mathrm{m}\angle 3=180°-\left(55+62\right)° \\ =63° \end{gathered}$$                                            مجموع زوايا المثلث الداخلية

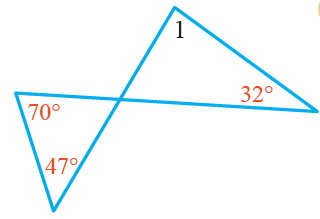
5)

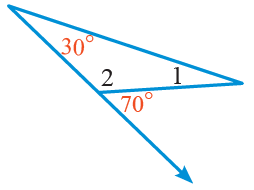
قياس الزاوية 1:

$$\begin{gathered} \mathrm{m}\angle 1=70°-30° \\ =40° \end{gathered}$$                                                         الزاوية °70 ، زاوية خارجية للمثلث ، ويساوي مجموع قياس الزاويتيين البعيدتين 

قياس الزاوية 2: 

$$\begin{gathered} \mathrm{m}\angle 3=180°-70° \\ =110° \end{gathered}$$                                                      زاويتان متجاورتان على مستقيمٍ 

6)

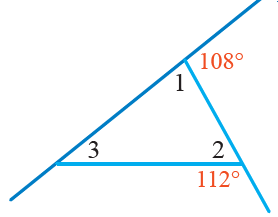
قياس الزاوية 1:

$$\begin{gathered} \mathrm{m}\angle 1=180°-108° \\ =72° \end{gathered}$$                                                    زاويتان متجاورتان على مستقيمٍ 

قياس الزاوية 2:

$$\begin{gathered} \mathrm{m}\angle 2=180°-112° \\ =68° \end{gathered}$$                                                    زاويتان متجاورتان على مستقيمٍ 

قياس الزاوية 3:

$$\begin{gathered} \mathrm{m}\angle 3=180°-\left(68+72\right)° \\ =40° \end{gathered}$$                                            مجموع زوايا المثلث الداخلية

 

7) جَبْرٌ: أصنِّفُ $\mathbf{△}\mathbf{QHD}$الى حاد الزوايا، أوْ قائمِ الزاويةِ، أوْ منفرِجِ الزاويةِ. 

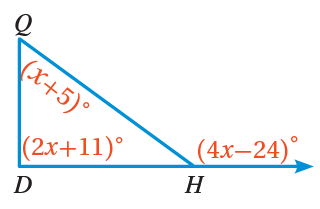
$\left(4\mathrm{x}-24\right)°=\left(\mathrm{x}+5\right)°+\left(2\mathrm{x}+11\right)°$                                  زاويةٌ خارجيةٌ للمثلثِ = مجموع الزاويتين الداخليتين البعيدتين 

$$\begin{gathered} \left(4\mathrm{x}-24\right)°=3\mathrm{x}+16° \\ \mathrm{x}=40° \end{gathered}$$                                  نجد قيمة x

نعوض x في المعادلات لإيجاد قيم الزاويا 

$$\begin{gathered} \mathrm{m}\angle \mathrm{Q}=45° \\ \mathrm{m}\angle \mathrm{D}=91° \\ \mathrm{m}\angle \mathrm{H}=180-\left(45+91\right)° \\ =44° \end{gathered}$$                                             الزاويتان H,Q حادتان ، والزاوية D منفرجة 

المثلث QHD مثلث منفرجة الزاوية 

 

8) إنشاءاتٌ: يمثلُ الشكلُ المجاورُ سِقالَةً تُستخدَمُ في أعمالِ البناءِ. أستعينُ بهِ لِيجادِ $\mathbf{m}\mathbf{\angle }\mathbf{1}$

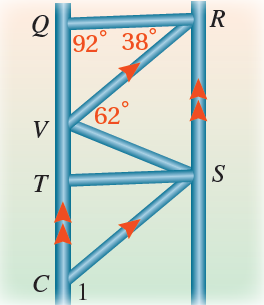
بما أن المستقيمات متوازية ويقطعهما مستقيم فإن الزاوية 1 تناظر الزاوية $\angle \mathrm{RVT}$ وهي زاوية خارجية للمثلث

$$\begin{gathered} \mathrm{m}\angle 1=92°+38° \\ =130° \end{gathered}$$                                                      زاويةٌ خارجيةٌ للمثلثِ = مجموع الزاويتين الداخليتين البعيدتين 

 

9) تبريرٌ: قالَتْ فاطمةُ: ان $\mathbf{m}\mathbf{\angle }\mathbf{BCD}\mathbf{=}\mathbf{20}\mathbf{°}$ لأن لها نفسَ قياسِ الزاويةِ المجاورةِ لها. لكنَّ ما قالتْهُ غيرُ صحيحٍ، أوضِّحُ لها كيفيَّةَ إيجادِ $\mathbf{m}\mathbf{\angle }\mathbf{BCD}$ مُبرِّرًا إجابتي

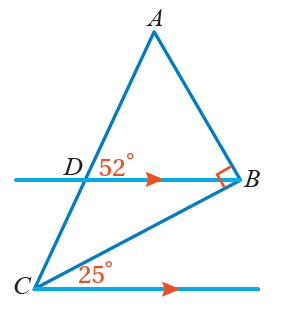
بما أن المستقيمات متوازية ويقطعها مستقيم فإن الزاوية $\angle \mathrm{ADB}$ تناظر الزاوية الخارجية $\angle \mathrm{BCD}+25°$ ومنه : 

$$\begin{gathered} \angle \mathrm{BCD}+25°=52° \\ \mathrm{m}\angle \mathrm{BCD}=27 \end{gathered}$$                                                   زاويةٌ خارجيةٌ للمثلثِ = مجموع الزاويتين الداخليتين البعيدتين 

 

 تبريرٌ: أعتمدُ على الشكلِ المجاورِ لإيجادِالزاويةِ التي تحقِّقُ الشرطَ المُعْطى، مُبرِّرًا إجابتي:

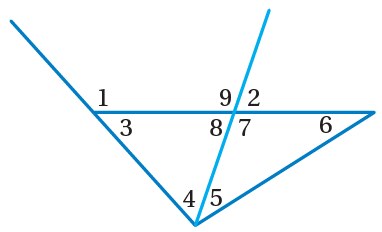
10) قياسُها أصغرُ منْ $\mathbf{m}\mathbf{\angle }\mathbf{2}$

الزاوية 5و6 ،التبرير: الزاوية 2 هي زاوية خارجية للمثلث الذي زاوياه 5,6,7 ، لذلك $\mathrm{m}\angle 2=\mathrm{m}\angle 6+\mathrm{m}\angle 5$

11) قياسُها أكبر منْ $\mathbf{m}\mathbf{\angle }\mathbf{4}$

الزاوية 9 ، التبرير: الزاوية 9 هي زاوية خارجية للمثلث الذي زاوياه 3,4,8 لذلك $\mathrm{m}\angle 9=\mathrm{m}\angle 3+\mathrm{m}\angle 4$

الزاوية 1 ، التبرير: الزاوية 1 هي زاوية خارجية للمثلث الذي زاوياه 3,4,8 لذلك $\mathrm{m}\angle 1=\mathrm{m}\angle 8+\mathrm{m}\angle 4$

الزاوية 7، التبرير: متقابلة بالرأس مع الزاوية 9

 

12) تبريرٌ: أحدِّدُ إذا كانَتِ العبارةُ المجاورةُ صحيحةً دائمًا، أوْ أحيانًا، أوْ غيرَ صحيحٍة أبدًا، مُبرِّرًا إجابتي. "مجموع قياسات الزوايا الخارجية عن المثلث °360""

صحيحة دائما لأن مجموع قياسات الزوايا الخارجة عن المثلث تساوي مجموع قياسات زوايا المثلث مرتين.

 

13) أكتبُُ أوضِّحُ مستعينًا بالرسمِ العلاقةَ بينَ أيِّ زاويةٍ خارجيةٍ للمثلثِ والزاويتينِ الداخليّتينِ غيرِ المجاورتينِ لها.

$$\begin{gathered} \mathrm{m}\angle 1=\mathrm{m}\angle \mathrm{B}+\mathrm{m}\angle \mathrm{C} \\ \mathrm{m}\angle 2=\mathrm{m}\angle \mathrm{A}+\mathrm{m}\angle \mathrm{C} \\ \mathrm{m}\angle 3=\mathrm{m}\angle \mathrm{A}+\mathrm{m}\angle \mathrm{B} \end{gathered}$$

---

---

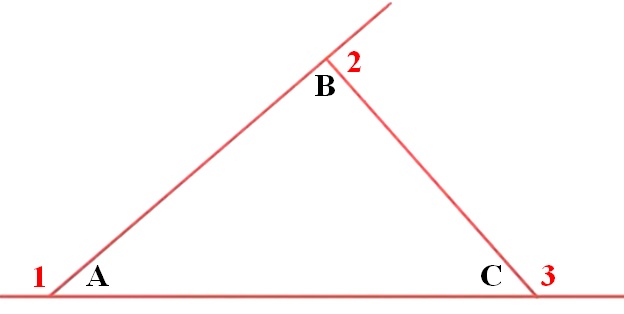
حلول أسئلة كتاب التمارين 

أجِدُ m∠1 في كُلٍّ منَ الأشْكالِ الآتِيةِ

1) 

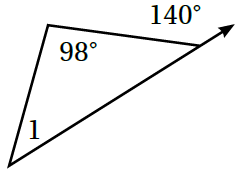
$$\begin{gathered} 140°=98+\mathrm{m}\angle 1 \\ \mathrm{m}\angle 1=42° \end{gathered}$$                                                      زاويةٌ خارجيةٌ للمثلثِ = مجموع الزاويتين الداخليتين البعيدتين 

2)

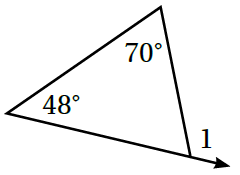
$$\begin{gathered} \mathrm{m}\angle 1=48°+70° \\ \mathrm{m}\angle 1=118° \end{gathered}$$                                                       زاويةٌ خارجيةٌ للمثلثِ = مجموع الزاويتين الداخليتين البعيدتين 

3)

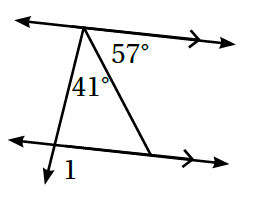
$$\begin{gathered} \mathrm{m}\angle 1=\left(57+41\right)° \\ =98° \end{gathered}$$                                                    بالتناظر مع مجموع الزاويتين   

4)

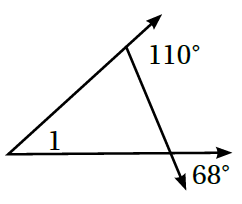
$$\begin{gathered} 110°=\mathrm{m}\angle 1+68° \\ \mathrm{m}\angle 1=42° \end{gathered}$$                                                       الزاوية 68 درجة متقابلة بالراس مع الزاوية الداخلية للمثلث ،

5)

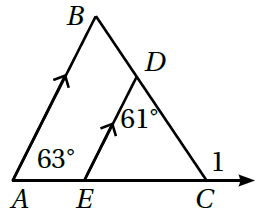
$\mathrm{m}\angle \mathrm{A}=\mathrm{m}\angle \mathrm{E}=63°$                                                     بالتناظر

$$\begin{gathered} \mathrm{m}\angle 1=\mathrm{m}\angle \mathrm{E}+\mathrm{m}\angle \mathrm{D} \\ =61°+63° \\ =124° \end{gathered}$$                                                  زاويةٌ خارجيةٌ للمثلثِ = مجموع الزاويتين الداخليتين البعيدتين 

6)

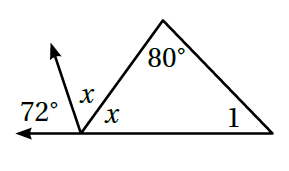
$$\begin{gathered} 180°=\mathrm{m}\angle \mathrm{x}+\mathrm{m}\angle \mathrm{x}+72° \\ \mathrm{m}\angle \mathrm{x}=54° \end{gathered}$$                                        الزاويتين x لهما نفس القياس ، وهما متكاملتين مع الزاوية 72 درجة          

$$\begin{gathered} \mathrm{m}\angle 1=180°-\left(80+54\right)° \\ =46° \end{gathered}$$                                         مجموع قياسات زوايا المثلث 

 

7)معتمدًا على الشّكلِ المُجاوِرِ، أجِدُ كُلًّ مِمّا يأْتي. وأبَرِّرُ إجابتِي.

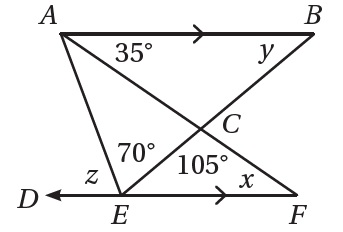
$$\begin{gathered} \mathbf{m}\mathbf{\angle }\mathbf{x} \\ \mathbf{x}\mathbf{=}35° \end{gathered}$$                                                                    التبرير:متبادلة داخليا مع $\angle \mathrm{BAF}$   

$\mathbf{m}\mathbf{\angle }\mathbf{y}$                                               

 $$\begin{gathered} \mathrm{m}\angle \mathrm{C}=180°-105° \\ \mathrm{m}\angle \mathrm{C}=75° \end{gathered}$$                                             التبرير: الزاوية C ، زاوية خارجية للمثلث ABC

$$\begin{gathered} \mathrm{m}\angle \mathrm{C}=\mathrm{y}+35° \\ \mathrm{y}=40° \end{gathered}$$

$\mathbf{m}\mathbf{\angle }\mathbf{z}$

$$\begin{gathered} \mathrm{z}+70°=105°+\mathrm{x} \\ \mathrm{m}\angle \mathrm{z}=70° \end{gathered}$$                                                  التبرير: الزاوية °70+z هي زاوية خارجية للمثلث ECF                                    

 

8) أتحَقّقُ منْ صِحّةِ خاصِّيّةِ الزّاويةِ الخارجيّةِ للمُثلَّثِ؛ مُعتمدًا على الشّكلِ المُجاورِ :

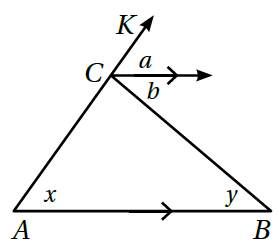
التبرير: بالتناظر                                 a=x

التبرير: متبادلتين داخلياً                    b=y

التبرير: الزاوية KCB تتكون $\mathrm{a},\mathrm{b}$          m∠KCB = a + b

أعوض: $\mathbf{b}\mathbf{=}\mathbf{y}\mathbf{,}\mathbf{x}\mathbf{=}\mathbf{a}$                         m∠KCB =x+y

 

9)أتحقّقُ منْ صِحّةِ خاصِّيّةِ مَجموعِ زَوايا المُثلَّثِ؛ مُعتمدًا عَلى الشّكلِ المُجاوِرِ:

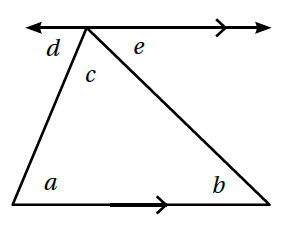
التبرير: متبادلتين داخلياً                                          a=d

التبرير: متبادلتين داخلياً                                         b=e

S هِي مَجموعُ زَوايا المُثلَّثِ الدّاخليّةِ              S=a+b+c

أعوِّضُ a = d , b = e                              $\mathbf{ }\mathbf{S}\mathbf{=}\mathbf{d}\mathbf{+}\mathbf{e}\mathbf{+}\mathbf{ }\mathbf{c}$

التبريرُ: زاويتان متجاورتان على مستقيمٍ        ° S =180