رياضيات فصل ثاني

حل المتباينات بالضرب والقسمة

حل أسئلة أتحقق من فهمي : 

أتحقق من فهمي : 

أحل كل متباينة مما يأتي وأمثل الحل على خط الأعداد ، ثم أتحقق من صحته : 

 3)  $\frac{\mathbf{y}}{\mathbf{3}}\mathbf{>}\mathbf{-}\mathbf{1}$       المتباينة الأصلية 

 

        $\mathbf{3}\mathbf{\left(}\frac{\mathbf{y}}{\mathbf{3}}\mathbf{\right)}\mathbf{>}\mathbf{3}\mathbf{(}\mathbf{-}\mathbf{1}\mathbf{)}$

          y > -3      حل المتباينة

 

التمثيل على خط الأعداد: 

أتحقق من صحة الحل : 

بما أن الحل  y > -3    أختار عدد أكبر من 3- 

مثلاً (  y = 1  )  وأعوضه في المتباينة الأصلية

$\frac{\mathrm{y}}{3}>-1\mathbf{ }$

$\frac{1}{3}>-1$

..............................................................................................................................................................................................................

4) $\frac{-4}{7}m<8$             المتباينة الأصلية

 

    $\left(\frac{-7}{4}\right)\left(\frac{-4}{7}\right)m<8\left(\frac{-7}{4}\right)$

 

       m > -14         حل المتباينة

 

التمثيل على خط الأعداد: 

أتحقق من صحة الحل : 

بما أن الحل  m > - 14  أختار عدد أكبر من  14-

مثلاً ( m = 1 )  وأعوضه في المتباينة الأصلية

$- \frac{4}{7}\mathrm{m}<8\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }$

$-\frac{4}{7}\left(1\right)<8$

$-\frac{4}{7}<8$       المتباينة صحيحة

..............................................................................................................................................................................................................

أتحقق من فهمي : 

أحل كل متباينة مما يأتي وأمثل الحل على خط الأعداد ، ثم أتحقق من صحة الحل: 

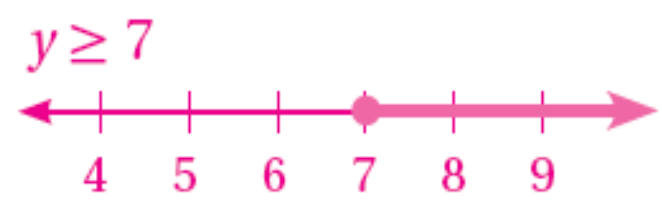
3)  4d < 8          المتباينة الأصلية

    $\frac{4\mathrm{d}}{4}<\frac{8}{4}$

     d < 2       حل المتباينة

التمثيل على خط الأعداد: 

أتحقق من صحة الحل : 

بما أن الحل  d < 2  أختار عدد أصغر من  2

مثلاً (  d = 1 )  وأعوضه في المتباينة الأصلية

4d < 8

4 ( 1 ) < 8

4 < 8           المتباينة صحيحة

.....................................................................................................................................................................................................................................

$\mathbf{4}\mathbf{)}\mathbf{ }-2y\le -14$

..............................................................................................................................................................................................................

أتحقق من فهمي : 

يتقاضى أحمد  2.5   عن كل ساعة عمل ،

أكتب متباينة وأحلها لايجاد عدد الساعات التي يجب أن يعمل فيها حتى يتقاضى  1100   على الأقل.

الحل: 

المعطيات: - يتقاضى أحمد في الساعة  2.5 JD

المطلوب:  كتابة متباينة وحلها حتى يتقاضى أحمد  400 JD على الأقل.

المتغير : أفرض  x  عدد ساعات العمل ، فيكون مقدار ما يتقاضى أحمد  2.5x

المتباينة: 

   $\mathbf{2}\mathbf{.}\mathbf{5}\mathbf{ }\mathbf{x}\mathbf{\ge }\mathbf{400}$

 

  $\frac{\mathbf{2}\mathbf{.}\mathbf{5}}{\mathbf{2}\mathbf{.}\mathbf{5}}\mathbf{x}\mathbf{\ge }\frac{\mathbf{400}}{\mathbf{2}\mathbf{.}\mathbf{5}}$

 

   $\mathbf{x}\mathbf{\ge }\mathbf{160}$

إذن يجب على أحمد أن يعمل  160  ساعة على الأقل.

..............................................................................................................................................................................................................

أتدرب وأحل المسائل : 

أحل كل متباينة مما يأتي ، وأمثل الحل على خط الأعداد ، ثم أتحقق من صحته : 

1) $\frac{\mathbf{u}}{\mathbf{3}}\mathbf{>}\mathbf{-}\mathbf{2}$               المتباينة الاصلية

 

$\mathbf{3}\mathbf{\left(}\frac{\mathbf{u}}{\mathbf{3}}\mathbf{\right)}\mathbf{>}\mathbf{3}\mathbf{ }\mathbf{(}\mathbf{-}\mathbf{2}\mathbf{)}\mathbf{ }$

 

u > - 6          حل المتباينة

 

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( u > -6)  أختار عدد أكبر من  6 -

مثلاً (u = -3 ) وأعوضه في المتباينة الأصلية 

$\frac{\mathbf{u}}{\mathbf{3}}\mathbf{>}\mathbf{-}\mathbf{2}$

 

$\frac{\mathbf{-}\mathbf{3}}{\mathbf{3}}\mathbf{>}\mathbf{-}\mathbf{2}$

 

$\mathbf{-}\mathbf{1}\mathbf{>}\mathbf{-}\mathbf{2}\mathbf{ }\mathbf{ }$              المتباينة صحيحة

...............................................................................................................................................................................................................

2)     $\mathbf{-}\mathbf{4}\mathit{x}\mathbf{\le }\mathbf{12}$                المتباينة الأصلية

 

       $\frac{\mathbf{-}\mathbf{4}\mathbf{x}}{\mathbf{-}\mathbf{4}}\mathbf{\ge }\frac{\mathbf{12}}{\mathbf{-}\mathbf{4}\mathbf{ }}$

         $\mathbf{x}\mathbf{\ge }\mathbf{-}\mathbf{3}\mathbf{ }$          حل المتباينة

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( $\mathbf{x}\mathbf{\ge }\mathbf{-}\mathbf{3}$)  أختار عدد أكبر من أو يساوي   3 -

مثلاً (x = -1 ) وأعوضه في المتباينة الأصلية 

$\mathbf{-}\mathbf{4}\mathit{x}\mathbf{\le }\mathbf{12}$                       المتباينة الأصلية

$\mathbf{-}\mathbf{4}\mathbf{(}\mathbf{-}\mathbf{1}\mathbf{)}\mathbf{\le }\mathbf{12}$

 $\mathbf{4}\mathbf{\le }\mathbf{12}$                    المتباينة صحيحة

..............................................................................................................................................................................................................

3)  $\mathbf{ }\frac{\mathbf{1}}{\mathbf{6}}\mathbf{t}\mathbf{ }\mathbf{<}\mathbf{-}\frac{\mathbf{1}}{\mathbf{3}}$              المتباينة الأصلية

 

       $\mathbf{6}\mathbf{\left(}\frac{\mathbf{1}}{\mathbf{6}}\mathbf{\right)}\mathbf{ }\mathbf{t}\mathbf{<}\mathbf{6}\mathbf{(}\mathbf{-}\frac{\mathbf{1}}{\mathbf{3}}\mathbf{)}$

 

        t < -2     حل المتباتينة

 

تمثيل المتباينة على خط الأعداد: 

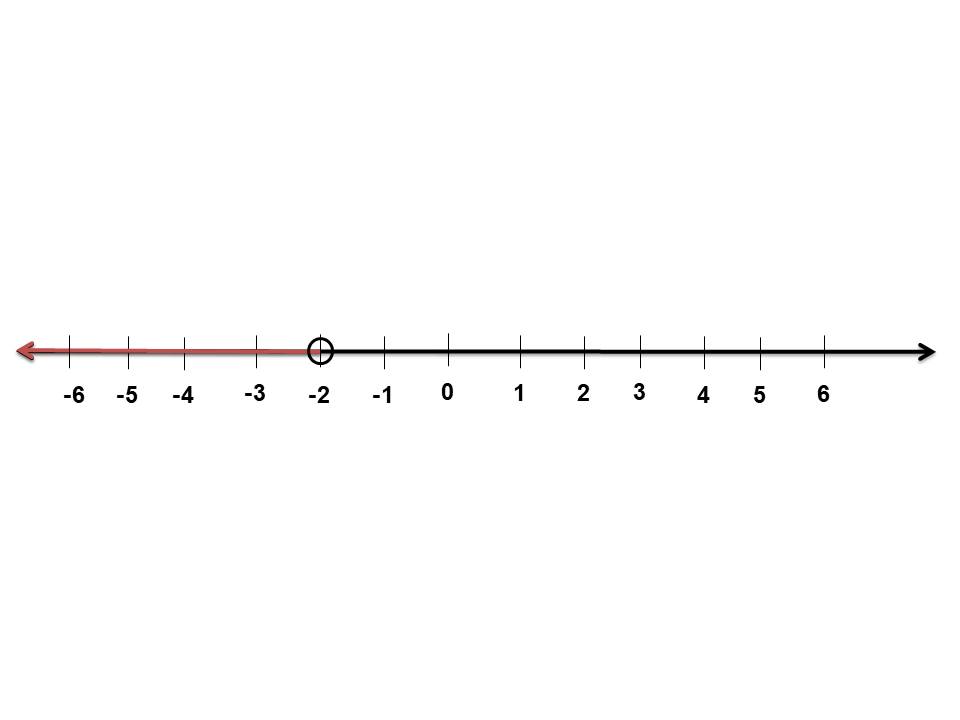
أتحقق من صحة المتباينة: 

بما أن الحل  ( t < -2)  أختار عدد أقل من  2 -

مثلاً (t = -8 ) أعوضه في المتباينة الأصلية 

$\frac{\mathbf{1}}{\mathbf{6}}\mathbf{t}\mathbf{<}\mathbf{-}\frac{\mathbf{1}}{\mathbf{3}}$            المتباينة الأصلية

$\frac{\mathbf{1}}{\mathbf{6}}\mathbf{(}\mathbf{-}\mathbf{8}\mathbf{)}\mathbf{<}\mathbf{-}\frac{\mathbf{1}}{\mathbf{3}}$

$\mathbf{-}\frac{\mathbf{8}}{\mathbf{6}}\mathbf{<}\mathbf{-}\frac{\mathbf{1}}{\mathbf{3}}$

 

$\mathbf{-}\frac{\mathbf{4}}{\mathbf{3}}\mathbf{<}\mathbf{-}\frac{\mathbf{1}}{\mathbf{3}}\mathbf{ }$   المتباينة صحيحة

..............................................................................................................................................................................................................

4) $\mathbf{ }\mathbf{-}\frac{\mathbf{2}}{\mathbf{5}}\mathbf{w}\mathbf{\ge }\mathbf{4}\mathbf{ }\mathbf{ }$    المتباينة الأصلية

 

   $\mathbf{-}\frac{\mathbf{5}}{\mathbf{2}}\mathbf{(}\mathbf{-}\frac{\mathbf{2}}{\mathbf{5}}\mathbf{w}\mathbf{)}\mathbf{\le }\mathbf{-}\frac{\mathbf{5}}{\mathbf{2}}\mathbf{\times }\mathbf{4}$

    $\mathbf{w}\mathbf{\le }\mathbf{-}\mathbf{10}\mathbf{ }$    حل المتباينة

تمثيل المتباينة على خط الأعداد: 

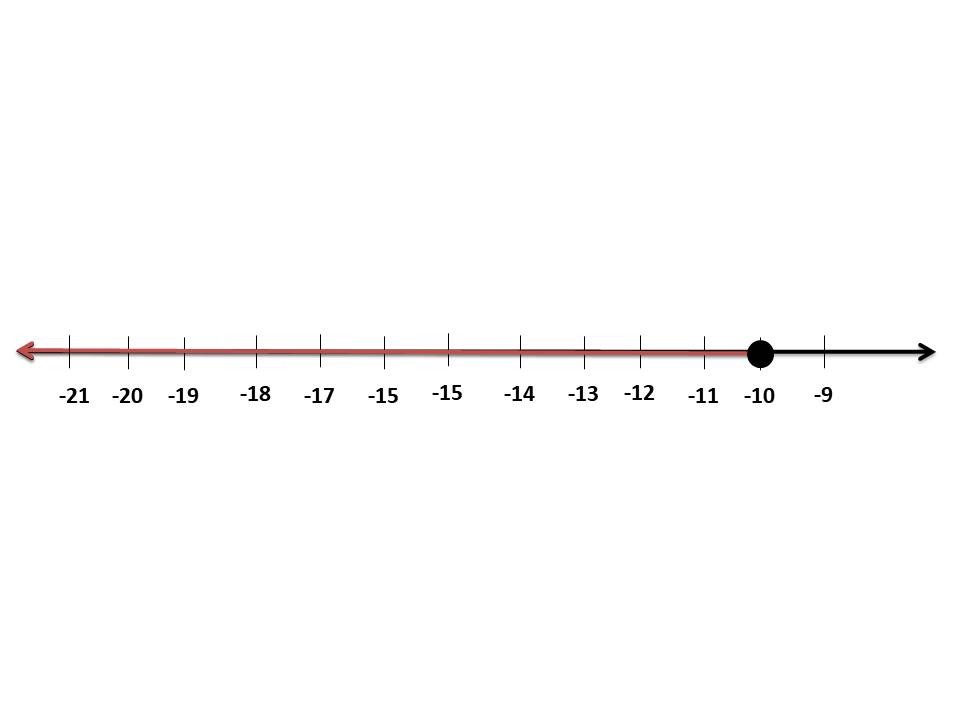
أتحقق من صحة المتباينة: 

بما أن الحل  ( $\mathbf{w}\mathbf{\le }\mathbf{-}\mathbf{10}$)  أختار عدد أقل من أو يساوي  10 -

مثلاً (w = -15 ) وأعوضه في المتباينة الأصلية 

$\mathbf{-}\frac{\mathbf{2}}{\mathbf{5}}\mathbf{w}\mathbf{\ge }\mathbf{4}$

$\mathbf{-}\frac{\mathbf{2}}{\mathbf{5}}\mathbf{(}\mathbf{-}\mathbf{15}\mathbf{)}\mathbf{\ge }\mathbf{4}$

$\mathbf{6}\mathbf{\ge }\mathbf{4}\mathbf{ }$       المتباينة صحيحة

 

..............................................................................................................................................................................................................

5) $\mathbf{ }\frac{\mathbf{n}}{\mathbf{5}}\mathbf{\le }\mathbf{0}\mathbf{.}\mathbf{8}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }$المتباينة الأصلية

 

$\mathbf{5}\mathbf{\left(}\frac{\mathbf{n}}{\mathbf{5}}\mathbf{\right)}\mathbf{\le }\mathbf{5}\mathbf{(}\mathbf{0}\mathbf{.}\mathbf{8}\mathbf{)}$

 

$\mathbf{n}\mathbf{\le }\mathbf{4}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }$  حل المتباينة

 

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( $\mathbf{n}\mathbf{\le }\mathbf{4}$)  أختار عدد أقل من أو يساوي  4

مثلاً (n = 1) وأعوضه في المتباينة الأصلية 

$\frac{\mathbf{n}}{\mathbf{5}}\mathbf{\le }\mathbf{0}\mathbf{.}\mathbf{8}\mathbf{ }\mathbf{ }\mathbf{ }$المتباينة الأصلية

$\frac{\mathbf{1}}{\mathbf{5}}\mathbf{\le }\mathbf{0}\mathbf{.}\mathbf{8}$

$\mathbf{0}\mathbf{.}\mathbf{2}\mathbf{\le }\mathbf{0}\mathbf{.}\mathbf{8}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }$المتباينة صحيحة

..............................................................................................................................................................................................................

6) $\mathbf{ }\mathbf{-}\mathbf{5}\mathbf{>}\frac{\mathbf{c}}{\mathbf{-}\mathbf{4}\mathbf{.}\mathbf{5}}\mathbf{ }\mathbf{ }\mathbf{ }$  المتباينة الأصلية

 

$\mathbf{-}\mathbf{4}\mathbf{.}\mathbf{5}\mathbf{ }\mathbf{(}\mathbf{-}\mathbf{5}\mathbf{)}\mathbf{<}\mathbf{-}\mathbf{4}\mathbf{.}\mathbf{5}\mathbf{\left(}\frac{\mathbf{ }\mathbf{c}}{\mathbf{-}\mathbf{4}\mathbf{.}\mathbf{5}}\mathbf{\right)}$

 

 22.5 < c   حل المتباينة

 

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( c > 22.5)  أختار عدد أكبر من  22.5

مثلاً ( c = 25) وأعوضه في المتباينة الأصلية 

$\mathbf{-}\mathbf{5}\mathbf{>}\frac{\mathbf{c}}{\mathbf{-}\mathbf{4}\mathbf{.}\mathbf{5}}\mathbf{ }\mathbf{ }$ المتباينة الأصلية

 

$\mathbf{-}\mathbf{5}\mathbf{>}\frac{\mathbf{25}}{\mathbf{-}\mathbf{4}\mathbf{.}\mathbf{5}\mathbf{ }}$

 

$\mathbf{-}\mathbf{5}\mathbf{>}\mathbf{-}\mathbf{5}\mathbf{.}\mathbf{5}\mathbf{ }$     المتباينة صحيحة

..............................................................................................................................................................................................................

أحل كل متباينة مما يأتي ، وأمثل الحل على خط الأعداد ، ثم أتحقق من صحته:

7)  $\mathbf{ }\mathbf{-}\mathbf{13}\mathbf{x}\mathbf{\ge }\mathbf{26}\mathbf{ }$    المتباينة الأصلية

 

        $\frac{\mathbf{-}\mathbf{13}\mathbf{x}}{\mathbf{-}\mathbf{13}}\mathbf{\le }\frac{\mathbf{26}}{\mathbf{-}\mathbf{13}}$

 

         $\mathbf{x}\mathbf{\le }\mathbf{-}\mathbf{2}\mathbf{ }\mathbf{ }$      حل المتباينة 

 

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( $\mathbf{x}\mathbf{\le }\mathbf{-}\mathbf{2}$)  أختار عدد أقل من أو يساوي   2-

مثلاً ( x = -3 ) وأعوضه في المتباينة الأصلية 

   $\mathbf{-}\mathbf{13}\mathit{x}\mathbf{\ge }\mathbf{26}\mathbf{ }$      المتباينة الأصلية

 

   $\mathbf{-}\mathbf{13}\mathbf{(}\mathbf{-}\mathbf{3}\mathbf{)}\mathbf{\ge }\mathbf{26}$

 

    $\mathbf{39}\mathbf{\ge }\mathbf{26}\mathbf{ }$         المتباينة صحيحة

..............................................................................................................................................................................................................

8)    $\mathbf{-}\mathbf{20}\mathbf{\le }\mathbf{10}\mathit{n}$                       المتباينة الأصلية  

   $\frac{\mathbf{-}\mathbf{20}}{\mathbf{10}}\mathbf{\le }\frac{\mathbf{10}\mathbf{n}}{\mathbf{10}}$

  $\mathbf{-}\mathbf{2}\mathbf{\le }\mathbf{n}$

   n $\mathbf{\ge }$-2                                   حل  المتباينة 

 

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( $\mathbf{n}\mathbf{\ge }\mathbf{-}\mathbf{2}$)  أختار عدد أكبر من أو يساوي  2 -

مثلاً ( n = 1 ) أعوضه في المتباينة الأصلية .

  $\mathbf{-}\mathbf{20}\mathbf{\le }\mathbf{10}\mathit{n}$              المتباينة الاصلية

 $\mathbf{-}\mathbf{20}\mathbf{\le }\mathbf{10}\mathbf{\left(}\mathbf{1}\mathbf{\right)}$

$\mathbf{-}\mathbf{20}\mathbf{\le }\mathbf{10}$                  المتباينة صحيحة 

..............................................................................................................................................................................................................

9 )  5b > - 15                   المتباينة الأصلية

    $\frac{\mathbf{5}\mathbf{b}}{\mathbf{5}}\mathbf{>}\frac{\mathbf{-}\mathbf{15}}{\mathbf{5}}$

      b > -3                         حل المتباينة

 

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( b > - 3)  أختار عدد أكبر من  3 -

مثلاً (b = -1 ) وأعوضه في المتباينة الأصلية

5b > -15         المتباينة الاصلية

$5(-1)>-15$

$-5>-15$              المتباينة صحيحة

..............................................................................................................................................................................................................

10)  144 < 12d               المتباينة الاصلية

 

$\frac{\mathbf{144}}{\mathbf{12}}\mathbf{<}\frac{\mathbf{12}\mathbf{d}}{\mathbf{12}}$

 

12 < d                             حل المتباينة

 

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( d > 12)  أختار عدد أكبر من  12

مثلاً (u = 14 ) وأعوضه في المتباينة الأصلية

144 < 12 d                  المتباينة الاصلية

144 < 12 ( 14 ) 

144 < 168                  المتباينة صحيحة

..............................................................................................................................................................................................................

11)  $-3m>-33$            المتباينة الأصلية

 

   $\frac{\mathbf{-}\mathbf{3}\mathbf{m}\mathbf{ }}{\mathbf{-}\mathbf{3}}\mathbf{<}\frac{\mathbf{-}\mathbf{33}}{\mathbf{-}\mathbf{3}}$

      m < 11                       حل المتباينة

 

تمثيل المتباينة على خط الأعداد: 

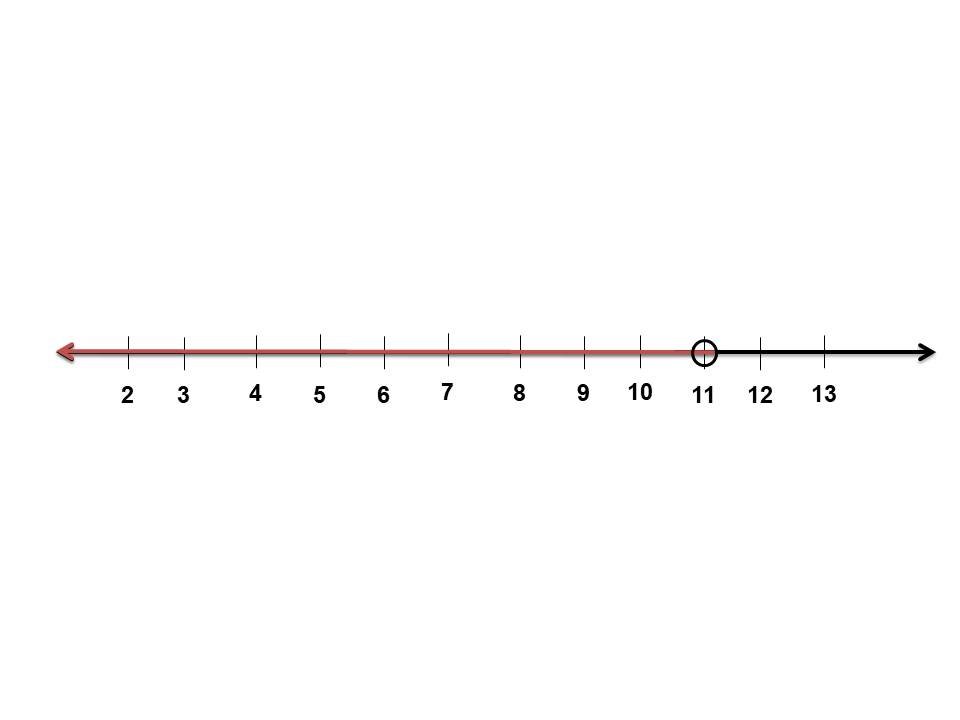
أتحقق من صحة المتباينة: 

بما أن الحل  ( m <  11 )  أختار عدد أقل من  11 

مثلاً (m = - 8 ) وأعوضه في المتباينة الأصلية

$-3m>-33$      المتباينة الأصلية

  $-3(-8)>-33$

     $24>-33$          المتباينة صحيحة

..............................................................................................................................................................................................................

12) $\mathbf{-}\mathbf{3}\mathbf{.}\mathbf{9}\mathit{c}\mathbf{\le }\mathbf{43}\mathbf{.}\mathbf{68}$ 

  

$\frac{\mathbf{-}\mathbf{ }\mathbf{3}\mathbf{.}\mathbf{9}\mathbf{ }\mathbf{c}}{\mathbf{-}\mathbf{ }\mathbf{3}\mathbf{.}\mathbf{9}}\mathbf{\ge }\frac{\mathbf{43}\mathbf{.}\mathbf{68}}{\mathbf{-}\mathbf{3}\mathbf{.}\mathbf{9}}$

 

$\mathbf{c}\mathbf{\ge }\mathbf{-}\mathbf{ }\mathbf{11}\mathbf{.}\mathbf{2}$         حل المتباينة

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( $\mathbf{c}\mathbf{\ge }\mathbf{-}\mathbf{11}\mathbf{.}\mathbf{2}$ )  أختار عدد أكبر من أو يساوي  11.2 -

مثلاً (m = -11 ) وأعوضه في المتباينة الأصلية

$\mathbf{-}\mathbf{ }\mathbf{3}\mathbf{.}\mathbf{9}\mathbf{c}\mathbf{\le }\mathbf{43}\mathbf{.}\mathbf{68}$

$\mathbf{-}\mathbf{3}\mathbf{.}\mathbf{9}\mathbf{(}\mathbf{-}\mathbf{11}\mathbf{)}\mathbf{\le }\mathbf{43}\mathbf{.}\mathbf{68}$

$\mathbf{42}\mathbf{.}\mathbf{9}\mathbf{\le }\mathbf{43}\mathbf{.}\mathbf{68}\mathbf{ }$             المتباينة صحيحة

........................................................................................................................................................................................................................................................................

اكتب متباينة تمثل كل جملة مما يأتي ثم أحلها: 

13) خمسة أمثال عدد أقل من 45

المتباينة :                     5x < 45

الحل: 

5x < 45         المتباينة الاصلية

$\frac{\mathbf{5}\mathbf{x}}{\mathbf{5}}\mathbf{ }\mathbf{<}\mathbf{ }\frac{\mathbf{45}}{\mathbf{5}}$

x < 9                حل المتباينة

........................................................................................................................................................................................................................................................................

14) عدد مقسوم على  4  لا يزيد على  8

المتباينة :                          $\frac{\mathbf{y}}{\mathbf{4}}\mathbf{ }\mathbf{\le }\mathbf{ }\mathbf{8}$

الحل: 

$\frac{\mathbf{y}}{\mathbf{4}}\mathbf{\le }\mathbf{8}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{الاصلية}\mathbf{ }\mathbf{المبتاينة}$

$\mathbf{4}\mathbf{\left(}\frac{\mathbf{y}}{\mathbf{4}}\mathbf{\right)}\mathbf{\le }\mathbf{4}\mathbf{\left(}\mathbf{8}\mathbf{\right)}$

 

$\mathbf{y}\mathbf{\le }\mathbf{32}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{المتباينة}\mathbf{ }\mathbf{حل}$

........................................................................................................................................................................................................................................................................

15) ثلاثة أمثال عدد أكبر من  18-

المتباينة:                         3a > - 18

الحل:

3a > - 18                المتباينة الأصلية

 

$\frac{\mathbf{3}\mathbf{a}}{\mathbf{3}}\mathbf{>}\frac{\mathbf{-}\mathbf{18}}{\mathbf{3}}$

  a > - 6                        حل المتباينة

........................................................................................................................................................................................................................................................................

16) عدد مقسوم على  2  لا يقل عن 5: 

المتباينة:                                  $\frac{\mathbf{m}}{\mathbf{2}}\mathbf{ }\mathbf{\ge }\mathbf{ }\mathbf{5}$

الحل:

$$\begin{gathered} \frac{\mathbf{m}}{\mathbf{2}}\mathbf{ }\mathbf{\ge }\mathbf{ }\mathbf{5}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{الاصلية}\mathbf{ }\mathbf{المتباينة} \\ \mathbf{2}\mathbf{ }\mathbf{(}\mathbf{ }\frac{\mathbf{m}}{\mathbf{2}}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{\ge }\mathbf{ }\mathbf{2}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{5}\mathbf{ }\mathbf{)} \end{gathered}$$

m   $\mathbf{\ge }$  10                          حل المتباينة     

........................................................................................................................................................................................................................................................................

17) مدارس :  مدرسة أساسية فيها  275  طالباً ، ثلاثة أخماسهم على الأقل في الصفوف الاساسية الدنيا.

اكتب متباينة وأحلها لأجد أقل عدد ممكن من الطلبة في الصفوف الاساسية الدنيا في المدرسة .

الحل:

المعطيات: - عدد طلاب المدرسة  275 طالباً 

                    - ثلاثة أخماس الطلاب على الاقل من الصفوف الاساسية الدنيا

المطلوب: كتابة متباينة وحلها لأجد أقل عدد ممكن من الطلبة في الصفوف الاساسية الدنيا.

المتغير : أفرض  x  عدد الطلاب في الصفوف الاساسية الدنيا

المتباينة: 

$\frac{3}{5}\mathrm{x}\ge 165$

$\mathrm{x}\ge 165\times \frac{5}{3}$

$x\ge 275$

 

إذن أقل عدد ممكن من الطلبة في الصفوف الاساسية الدنيا هو 275 طالباً .

........................................................................................................................................................................................................................................................................

18) حديقة : يريد طارق تبليط منطقة مستطيلة الشكل في حديقة منزله مساحتها   m² 15 ، ويملك فقط  75 JD

اكتب متباينة وأحلها ، لتمثل ثمن المتر المربع الواحد من البلاط الذي يمكن لطارق أن يشتريه. 

الحل: 

المعطيات: - حديقة مستطيلة الشكل 

                    - مساحة الحديقة 15m² 

                  - يملك  طارق   75   JD 

المطلوب : كتابة متباينة تمثل ثمن المتر المربع الواحد من البلاط الذي يمكن لطارق أن يشتريه وحلها.

المتغير : أفرض  y ثمن المتر المربع الواحد 

المتباينة :

$\mathbf{15}\mathbf{y}\mathbf{\le }\mathbf{75}$

 

$\frac{\mathbf{15}\mathbf{ }\mathbf{y}}{\mathbf{15}}\mathbf{\le }\frac{\mathbf{75}}{\mathbf{15}}$

 

$\mathbf{y}\mathbf{\le }\mathbf{5}\mathbf{ }$

إذن يمكن لطارق دفع مبلع لا يزيد عن 5 دنانير  ثمن المتر المربع الواحد من البلاط

........................................................................................................................................................................................................................................................................

19) أعود الى فقرة ( استكشف ) بداية الدرس ، وأحل المسألة.

الحل:

المعطيات: علامتي كمال في الاختبار الاول والثاني   93 ، 90

المطلوب : الحد الادنى للعلامة التي يجب أن يحصل عليها في الاختبار الثالث ليكون معدل علاماته  90  على الاقل

المتغير : أفرض m  علامة الاختبار الثالث.

المتباينة: 

$$\begin{gathered} \frac{\mathbf{90}\mathbf{+}\mathbf{93}\mathbf{ }\mathbf{m}}{\mathbf{3}}\mathbf{\ge }\mathbf{90} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \end{gathered}$$

$\mathbf{3}\mathbf{\left(}\frac{\mathbf{90}\mathbf{+}\mathbf{93}\mathbf{m}}{\mathbf{3}}\mathbf{\right)}\mathbf{\ge }\mathbf{3}\mathbf{(}\mathbf{90}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }$

 

$\mathbf{90}\mathbf{+}\mathbf{93}\mathbf{+}\mathbf{m}\mathbf{\ge }\mathbf{270}\mathbf{ }\mathbf{ }$

 

$\mathbf{183}\mathbf{+}\mathbf{m}\mathbf{\ge }\mathbf{270}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }$

 

$\mathbf{183}\mathbf{+}\mathbf{m}\mathbf{-}\mathbf{183}\mathbf{\ge }\mathbf{270}\mathbf{-}\mathbf{183}$

 

$\mathbf{m}\mathbf{\ge }\mathbf{87}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{المبتاينة}\mathbf{ }\mathbf{حل}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }$

إذن أقل علامة على كمال أن يحصل عليها هي  87 

........................................................................................................................................................................................................................................................................

20) مسألة مفتوحة : أكتب متباينة يمكن حلها بالقسمة على عدد سالب وحلها   $\mathbf{x}\mathbf{ }\mathbf{\ge }\mathbf{ }\frac{\mathbf{1}}{\mathbf{4}}$

الحل: 

$\mathbf{x}\mathbf{\ge }\frac{\mathbf{1}}{\mathbf{4}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{الاصلية}\mathbf{ }\mathbf{المتباينة}$

$\mathbf{-}\mathbf{2}\mathbf{x}\mathbf{\le }\mathbf{(}\mathbf{-}\mathbf{2}\mathbf{)}\mathbf{ }\mathbf{\left(}\frac{\mathbf{1}}{\mathbf{4}}\mathbf{\right)}\mathbf{ }$                  -2 نضرب طرفي المتباينة بعدد سالب مثلا

$\mathbf{-}\mathbf{2}\mathbf{x}\mathbf{\le }\mathbf{-}\frac{\mathbf{1}}{\mathbf{2}}$                      المتباينة المطلوبة 

........................................................................................................................................................................................................................................................................

21)  تبرير : اكتب متباينة وأحلها لتمثل المحيط الممكن للدائرة المجاورة ، وأبرر اجابتي.

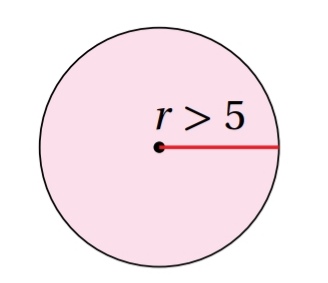
الحل:

المعطيات: - نصف القطر     ( r > 5 ) 

المطلوب : كتابة متباينة وحلها لتمثل المحيط الممكن للدائرة .

أعلم أن محيط الدائرة يعطى بالعلاقة  $\mathit{c}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{2}\mathit{\pi }\mathit{r}$   

بما أن: 

r > 5

$\mathbf{2}\mathbf{\pi r}\mathbf{>}\mathbf{(}\mathbf{ }\mathbf{2}\mathbf{\pi }\mathbf{)}\mathbf{\left(}\mathbf{5}\mathbf{\right)}\mathbf{ }$

$\mathbf{c}\mathbf{>}\mathbf{10}\mathbf{\pi }$

 

........................................................................................................................................................................................................................................................................

22) اكتشف الخطأ : انظر الحل الاتي ، واكتشف الخطأ الوارد فيه ، ثم أصححه .

الحل: 

الخطأ : عند ضرب طرفي المتباينة بعدد موجب لا نغير رمز المتباينة 

المتباينة الأصلية : 

$\mathbf{-}\mathbf{6}\mathbf{>}\frac{\mathbf{2}}{\mathbf{3}}\mathbf{x}$

$\frac{\mathbf{3}}{\mathbf{2}}\mathbf{(}\mathbf{-}\mathbf{6}\mathbf{)}\mathbf{>}\frac{\mathbf{3}}{\mathbf{2}}\mathbf{\left(}\frac{\mathbf{2}}{\mathbf{3}}\mathit{x}\mathbf{\right)}$

$\frac{\mathbf{-}\mathbf{18}}{\mathbf{2}}\mathbf{>}\mathit{x}$

$\mathbf{-}\mathbf{9}\mathbf{>}\mathbf{x}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{المتباينة}\mathbf{ }\mathbf{حل}$

........................................................................................................................................................................................................................................................................

23) اكتب:  كيف استعمل خاصيتي الضرب والقسمة للمتباينات في حل متباينة؟ 

الحل : 

استعمل خاصيتي الضرب والقسمة للمتباينة لعزل المتغير في طرف لوحده :

1- عند الضرب بعدد موجب أو القسمة عليه نحافظ على رمز المتباينة كما هو .

2- عند الضرب بعدد سالب أو القسمة عليه نغير اتجاه رمز المتباينة .

........................................................................................................................................................................................................................................................

حل مسائل كتاب التمارين : 

اكتب <  أو  >  أو  $\mathbf{\ge }$ أو $\mathbf{\le }$ في الفراغ  لأكون عبارة صحيحة في ما يأتي: 

1)  إذا كان    b > 7      فإن :     3b  $\mathbf{>}$ 21

2) إذا كان     u < 0      فإن:       u  $\mathbf{<}$  0-

3) إذا كان    $\frac{\mathbf{1}}{\mathbf{2}}\mathbf{y}\mathbf{ }\mathbf{\ge }\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{5}$       فإن:         y  $\mathbf{\ge }$  -10

4) إذا كان        3t   $\mathbf{\le }$  18-     فإن:         t   $\mathbf{\ge }$   -6

........................................................................................................................................................................................................................................................

أحل المتباينات الآتية ، وأمثلها بيانياً ، وأتحقق من صحة الحل: 

 $\mathbf{5}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{5}\mathbf{ }\mathbf{\le }\frac{\mathbf{1}}{\mathbf{4}}\mathit{y}$

$\mathbf{4}\mathbf{(}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{5}\mathbf{ }\mathbf{)}\mathbf{\le }\mathbf{4}\mathbf{\left(}\frac{\mathbf{1}}{\mathbf{4}}\mathit{y}\mathbf{\right)}$

$\mathbf{2}\mathbf{\le }\mathit{y}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{المتباينة}\mathbf{ }\mathbf{حل}\mathbf{ }$

 

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( $\mathbf{y}\mathbf{ }\mathbf{\ge }\mathbf{ }\mathbf{2}$)  أختار عدد أكبر من أو يساوي  2

مثلاً ( y = 4  ) وأعوضه في المتباينة الأصلية

$\mathbf{0}\mathbf{.}\mathbf{5}\mathbf{\le }\frac{\mathbf{1}}{\mathbf{4}}\mathbf{y}$

$\mathbf{0}\mathbf{.}\mathbf{5}\mathbf{\le }\frac{\mathbf{1}}{\mathbf{4}}\mathbf{\left(}\mathbf{4}\mathbf{\right)}\mathbf{ }$

$\mathbf{0}\mathbf{.}\mathbf{5}\mathbf{\le }\mathbf{1}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{صحيحة}\mathbf{ }\mathbf{المتباينة}$

........................................................................................................................................................................................................................................................................

6)    $-12>3x$            المتباينة الأصلية

     $\frac{\mathbf{-}\mathbf{12}}{\mathbf{3}}\mathbf{>}\frac{\mathbf{3}\mathbf{x}}{\mathbf{3}}$

   $-4>x$                    حل المتباينة

 

تمثيل المتباينة على خط الأعداد: 

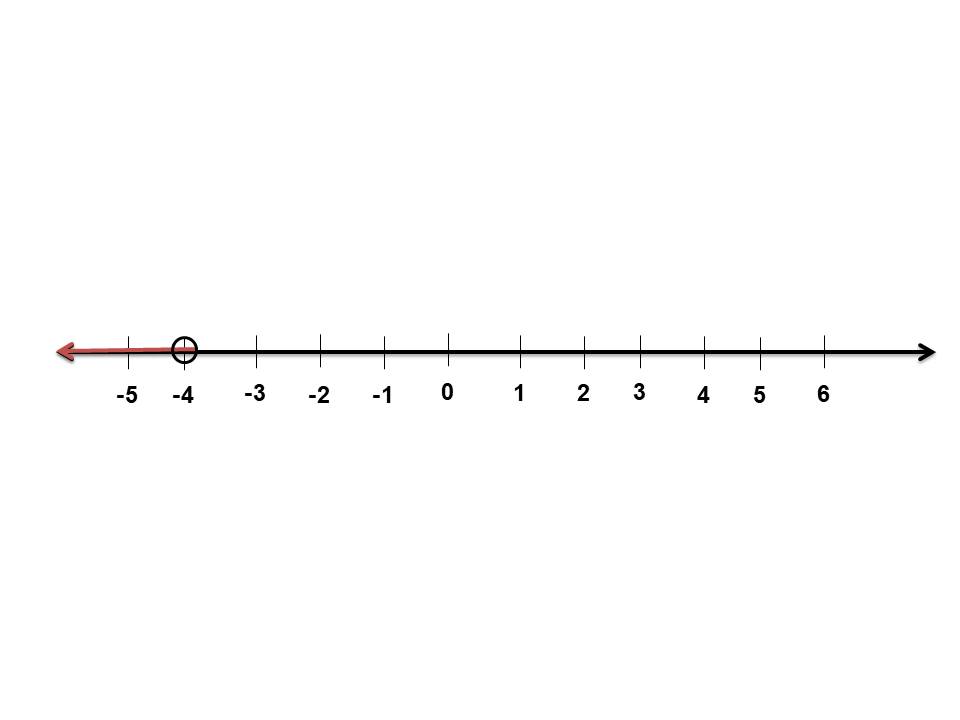
أتحقق من صحة المتباينة: 

بما أن الحل  ( x < -4)  أختار عدد أقل من  4 -

مثلاً (x = -5 ) وأعوضه في المتباينة الأصلية

$-12>3x$             المتباينة الاصلية

$-12>3(-5)$

$-12>-15$             المتباينة صحيحة

........................................................................................................................................................................................................................................................................

$\mathbf{7}\mathbf{)}\mathbf{ }\mathbf{ }\frac{\mathbf{2}}{\mathbf{5}}\mathbf{h}\mathbf{<}\mathbf{10}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{الاصلية}\mathbf{ }\mathbf{المتباينة}$

    $\frac{\mathbf{5}}{\mathbf{2}}\mathbf{\left(}\frac{\mathbf{2}}{\mathbf{5}}\mathbf{\right)}\mathbf{ }\mathbf{h}\mathbf{<}\frac{\mathbf{5}}{\mathbf{2}}\mathbf{\left(}\mathbf{10}\mathbf{\right)}$

     h < 25                              حل المتباينة

 

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( h < 25)  أختار عدد أقل من  25

مثلاً ( h = 20  ) وأعوضه في المتباينة الأصلية

$\frac{\mathbf{2}}{\mathbf{5}}\mathbf{ }\mathbf{h}\mathbf{<}\mathbf{10}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }$

$\frac{\mathbf{2}}{\mathbf{5}}\mathbf{\left(}\mathbf{20}\mathbf{\right)}\mathbf{<}\mathbf{10}$

8 < 10                           المتباينة صحيحة

........................................................................................................................................................................................................................................................................

8)  $\mathbf{-}\mathbf{3}\mathbf{.}\mathbf{5}\mathbf{>}\mathbf{7}\mathit{b}$               المتباينة الاصلية

$\frac{\mathbf{ }\mathbf{-}\mathbf{3}\mathbf{.}\mathbf{5}\mathbf{ }}{\mathbf{7}}\mathbf{>}\frac{\mathbf{7}\mathbf{ }\mathbf{b}}{\mathbf{7}}$

$\frac{\mathbf{-}\mathbf{ }\mathbf{1}}{\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{2}\mathbf{ }}\mathbf{>}\mathbf{b}$

$\mathbf{-}\mathbf{0}\mathbf{.}\mathbf{5}\mathbf{>}\mathbf{b}$                          حل المتباينة

 

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( b > - 0.5)  أختار عدد أقل من  0.5 -

مثلاً (b = -1 ) وأعوضه في المتباينة الأصلية

$-3.5>7b$

$-3.5>7(-1)$

$-3.5>-7$                   المتباينة صحيحة

.......................................................................................................................................................................................................................................................................

.$\mathbf{9}\mathbf{)}\mathbf{ }\mathbf{-}\frac{\mathbf{3}}{\mathbf{5}}\mathbf{\ge }\frac{\mathbf{w}}{\mathbf{5}}\mathbf{ }\mathbf{ }$

$\mathbf{5}\mathbf{(}\mathbf{-}\frac{\mathbf{3}}{\mathbf{5}}\mathbf{)}\mathbf{\ge }\mathbf{5}\mathbf{\left(}\frac{\mathbf{w}}{\mathbf{5}}\mathbf{\right)}$

$\mathbf{-}\mathbf{3}\mathbf{\ge }\mathbf{w}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{المتباينة}\mathbf{ }\mathbf{حل}$

تمثيل المتباينة على خط الأعداد: 

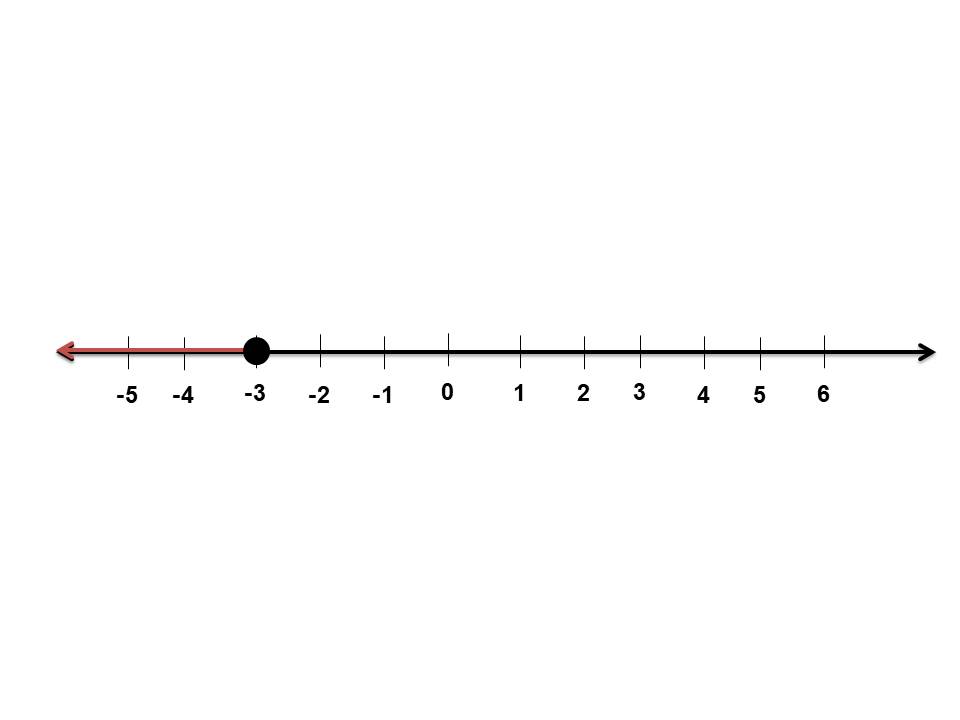
أتحقق من صحة المتباينة: 

بما أن الحل  ( $\mathbf{w}\mathbf{ }\mathbf{\le }\mathbf{ }\mathbf{-}\mathbf{3}$)  أختار عدد أصغر من أو يساوي  3 -

مثلاً (b = --5 ) وأعوضه في المتباينة الأصلية

$\mathbf{-}\frac{\mathbf{3}}{\mathbf{5}}\mathbf{\ge }\frac{\mathbf{w}}{\mathbf{5}}$

$\mathbf{-}\frac{\mathbf{3}}{\mathbf{5}}\mathbf{\ge }\frac{\mathbf{-}\mathbf{5}}{\mathbf{5}}$

$\mathbf{-}\mathbf{0}\mathbf{.}\mathbf{6}\mathbf{ }\mathbf{\ge }\mathbf{-}\mathbf{1}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{صحيحة}\mathbf{ }\mathbf{المتباينة}$

........................................................................................................................................................................................................................................................................

$\mathbf{10}\mathbf{)}\mathbf{ }\mathbf{-}\frac{\mathbf{9}}{\mathbf{4}}\mathbf{<}\mathbf{-}\frac{\mathbf{3}}{\mathbf{8}}\mathbf{b}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{الاصلية}\mathbf{ }\mathbf{المتباينة}$

$\mathbf{-}\frac{\mathbf{8}}{\mathbf{3}}\mathbf{(}\mathbf{-}\frac{\mathbf{9}}{\mathbf{4}}\mathbf{)}\mathbf{>}\mathbf{-}\frac{\mathbf{8}}{\mathbf{3}}\mathbf{ }\mathbf{(}\mathbf{-}\mathbf{ }\frac{\mathbf{3}}{\mathbf{8}}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{b}$

$\frac{\mathbf{72}}{\mathbf{12}}\mathbf{>}\mathbf{b}$

6 >  b                       حل المتباينة

 

تمثيل المتباينة على خط الأعداد: 

أتحقق من صحة المتباينة: 

بما أن الحل  ( b < 6 )  أختار عدد أقل من  6

مثلاً (b = 2 ) وأعوضه في المتباينة الأصلية

$\mathbf{-}\frac{\mathbf{9}}{\mathbf{4}}\mathbf{<}\mathbf{-}\frac{\mathbf{3}}{\mathbf{8}}\mathbf{b}$

$\mathbf{-}\frac{\mathbf{9}}{\mathbf{4}}\mathbf{<}\mathbf{-}\frac{\mathbf{3}}{\mathbf{8}}\mathbf{(}\mathbf{ }\mathbf{2}\mathbf{)}$

$\mathbf{-}\mathbf{2}\mathbf{.}\mathbf{25}\mathbf{<}\mathbf{-}\frac{\mathbf{6}}{\mathbf{8}}$

$\mathbf{-}\mathbf{2}\mathbf{.}\mathbf{25}\mathbf{<}\mathbf{-}\mathbf{0}\mathbf{.}\mathbf{75}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{صحيحة}\mathbf{ }\mathbf{المتباينة}$

........................................................................................................................................................................................................................................................................

11 ) صناعات غذائية : يبلغ معدل إنتاج مصنع من الألبان  120  علبة في الساعة ، ويخطط قسم الانتاج في المصنع 

لانتاج مالا يقل عن  600  علبة يومياً ، 

اكتب متباينة وأحلها لأجد الحد الأدنى من الساعات اليومية التي يجب أن يعمل بها المصنع لإنتاج الكمية المطلوبة.

الحل: 

المعطيات : - معدل الانتاج  120  علبة في الساعة 

المطلوب : كتابة متباينة وحلها لايجاد الحد الادنى من عدد ساعات العمل لانتاج مالا يقل عن  600  علبة يومياً 

المتغير : أفرض  x  عدد ساعات العمل 

المتباينة : 

120x $\mathbf{\ge }$   600

$\frac{\mathbf{120}\mathbf{x}}{\mathbf{120}}\mathbf{\ge }\frac{\mathbf{600}}{\mathbf{120}}$

$\mathbf{x}\mathbf{\ge }\mathbf{5}$

إذن الحد الادنى لعدد ساعات العمل 5  ساعات يومياً .

........................................................................................................................................................................................................................................................................

12) هندسة: مستطيل مساحته أقل من  85cm²   وطوله  20cm    . أكتب متباينة تمثل العرض الممكن للمستطيل ثم أحلها.

الحل : 

المعطيات : - مساحة المستطيل أقل من  85cm²

                     - طول المستطيل    20cm

المطلوب : كتابة متباينة تمثل العرض الممكن للمستطيل ثم أحلها.

المتغير : أفرض ان n  عرض المستطيل.

المتباينة: 

$\mathbf{20}\mathbf{ }\mathbf{n}\mathbf{<}\mathbf{85}$

$\frac{\mathbf{20}\mathbf{ }\mathbf{n}}{\mathbf{20}}\mathbf{<}\frac{\mathbf{85}}{\mathbf{20}}$

$\mathbf{n}\mathbf{<}\mathbf{4}\mathbf{.}\mathbf{25}$

أي أن العرض الممكن أقل من  4.25 cm

 

........................................................................................................................................................................................................................................................................

أبين ما إذا كانت كل من العبارات الآتية صحيحة دائماً أحياناً أم غير صحيحة أبداً ، موضحاً ذلك بأمثلة مناسبة: 

13 )  إذا كان $\mathbf{a}\mathbf{ }\mathbf{<}\mathbf{ }\mathbf{1}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{x}\mathbf{ }\mathbf{>}\mathbf{ }\mathbf{4}$  فإن ax > 0

صحيحة أحياناً :

مثال ( 1 ) : 

أختار مثلاً  (x = 5)  ،  ($\frac{\mathbf{1}}{\mathbf{2}}$ = a)   وأعوض في المتباينة الأصلية

ax > 0                  المتباينة الأصلية

$\frac{\mathbf{1}}{\mathbf{2}}\mathbf{\left(}\mathbf{4}\mathbf{\right)}\mathbf{>}\mathbf{0}$

$\mathbf{2}\mathbf{>}\mathbf{0}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{صحيحة}\mathbf{ }\mathbf{المتباينة}$

مثال ( 2 ) : 

أختار مثلاً ( x = 6 ) ،  ( a = -1 )  

ax > 0                 المتباينة الأصلية

$(-1)\left(6\right)>0$

$-6>0$               المتباينة خاطئة

........................................................................................................................................................................................................................................................................

14 ) إذا كان $\mathbf{b}\mathbf{<}\mathbf{0}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{x}\mathbf{<}\mathbf{0}$، فإن  bx > 0

صحيحة دائماً ، لأن حاصل ضرب العددين السالبين موجب دوماً 

مثال: 

أختار  مثلاً ( x ´= -1  )  ، (  b = -2 )   وأعوض في المتباينة 

bx > 0                  المتباينة الاصلية

( -2) ( -1 ) > 0

2 > 0

........................................................................................................................................................................................................................................

 

 

 

 

 

 

15 ) إذا كان $\mathbf{c}\mathbf{>}\mathbf{1}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{x}\mathbf{\ge }\mathbf{0}$   ، فإن  cx > 0

صحيحة أحياناً : 

مثال ( 1 ) :  أختار مثلاً  ( $\mathbf{x}\mathbf{=}\frac{\mathbf{1}}{\mathbf{2}}$ ) ، ( c = 1  ) وأعوض في المتباينة

cx > 0             المتباينة الاصلية

$2\left(1\right)>0$

2 > 0              المتباينة صحيحة

مثال ( 2 ) : أختار مثلاً ( x = 0 ) ، ( c = 3 )  وأعوض في المتباينة الأصلية

cx > 0 

( 3 ) ( 0 ) > 0

0 > 0          المتباينة خاطئة

..............................................................................................................................................................................................................

16) إذا كان $\mathbf{d}\mathbf{\ge }\mathbf{1}\mathbf{ }\mathbf{,}\mathbf{x}\mathbf{>}\mathbf{0}$  ، فإن  dx > 0

صحيحة دوماً 

لأن حاصل ضرب عددين موجبين هو عدد موجب دوماً 

مثال: أختار مثلاً ( x = 1 )   ، (  d = 2 )  وأعوض في المتباينة الاصلية 

dx > 0 

$2\left(1\right)>0$

$2>0$          المتباينة صحيحة

..............................................................................................................................................................................................................