رياضيات فصل أول

حل المعادلات التربيعية بيانيًا 

المُعادلةُ التربيعيَّةُ : مُعادلةٌ يمكنُ كتابتُها على الصورةِ : $a{x}^2+bx+c =0$  ، حيث a ≠ 0 ، والتي تُسَمّى الصورةَ القياسيَّةَ للمُعادلةِ التربيعيَّةِ، ولكلِّ

مُعادلةٍ تربيعيَّةٍ اقترانٌ تربيعيٌّ مُرتبطٌ بها يمكنُ الحصولُ عليهِ باستبدالِ (f(x بالعددِ 0.

يُمكن حلُّ المُعادلة التربيعيَّة بتحديد قِيَم x التي يقطعُ عندها منحنى الاقتران التربيعيِّ المُرتبط بالمُعادلة المحور x ، وَتُسَمّى تلك القِيَم جذور

المُعادلة أو أصفار الاقتران.  

•• يمكنُ حلُّ المُعادلة التربيعيَّة بيانيًّا باتِّباع الخُطوات الآتية :

مفهوم أساسيّ (حلّ المُعادلة التربيعيَّة بيانيًّا)

الخطوة 1 : أكتبُ المُعادلة بالصورة القياسيَّة  $a{x}^2+bx+c =0$

الخطوة 2 : أُمَثِّل بيانيًّا الاقتران التربيعيَّ المُرتبط بالمُعادلة وهو :  $f\left(x\right) = a{x}^2+bx+c$

الخطوة 3 : أجد قِيم x التي يقطع عندها منحنى الاقتران المُرتبط المحور x، إن وُجدت، وهي أصفار

الاقتران المُرتبط ، التي تُعَدُّ حلولَ المُعادلة.

حلُّ المُعادلةِ التربيعيَّةِ بيانِيًّا

يوجد جذران للمعادلة	يوجد جذر واحد	لا يوجد حل للمعادلة
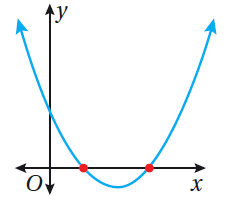
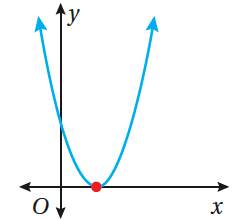