رياضيات فصل أول

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 135

أَحُلّ كُلًّ من المُعادلات الآتية بالقانونِ العامِّ، مُقَرِّبًا إجابتي لأقرب جُزءٍ من عشرة (إن لَزِم) :

a) 3x² + 16x = -5                                                          b) x² - 2x = 4

الحل : 

الخُطوة 1 : أكتبُ المُعادلةَ بالصورةِ القياسيَّةِ.

المُعادلةُ المُعطاةُ	3x2 + 16x = -5
بجمع 5 إلى طَرَفَيِ المُعادلة	3x2 + 16x + 5 = 0

الخُطوةُ 2 : أُطَبِّقُ القانونَ العامَّ.

صيغةُ القانونِ العامِّ	$x=\frac{-b\pm \sqrt[]{b^2-4ac}}{2a}$
بتعويضِ $a=3,b=16,c=5$	$x=\frac{-16\pm \sqrt[]{{16}^2-4\left(3\right)\left(5\right)}}{2\left(3\right)}$
بالتبسيطِ	$x=\frac{-16\pm \sqrt[]{256-60} }{6}$
بالجمعِ، ثمَّ إيجادِ الجذرِ التربيعيِّ	$x=\frac{-16\pm \sqrt[]{196}}{6}=\frac{-16\pm 14}{6}$
بفصلِ الحلَّيْنِ	$x=\frac{-16+14}{6} or x=\frac{-16-14}{6}$
بالتبسيط	$x=-\frac{1}{3} or x=-5$

إذن جذرا المعادلة هما :  $-\frac{1}{3} , -5$

---

b) x² - 2x = 4 

الخُطوة 1 : أكتبُ المُعادلةَ بالصورةِ القياسيَّةِ.

المُعادلةُ المُعطاةُ	x2 - 2x = 4
بطرح 4 من طَرَفَيِ المُعادلة	x2 - 2x - 4 = 0

الخُطوةُ 2 : أُطَبِّقُ القانونَ العامَّ.

صيغةُ القانونِ العامِّ	$x=\frac{-b\pm \sqrt[]{b^2-4ac}}{2a}$
بتعويضِ $a = 1 , b = -2 , c = -4$	$x=\frac{-(-2)\pm \sqrt[]{{(-2)}^2-4\left(1\right)(-4)}}{2\left(1\right)}$
بالتبسيطِ	$x=\frac{2\pm \sqrt[]{4+16} }{2}$
بالجمعِ	$x=\frac{2\pm \sqrt[]{20}}{2}$
بفصلِ الحلَّيْنِ	$x=\frac{2+\sqrt[]{20} }{2} or x=\frac{2-\sqrt[]{20}}{2}$
باستخدام الآلة الحاسبة	$x\approx 3.25 or x\approx -1.25$

إذن جذرا المعادلة التقريبيين هما : $3.25 , - 1.25$

---

أتحقق من فهمي صفحة 137

أُحَدِّدُ عددَ الحُلولِ الحقيقيَّةِ لكلِّ مُعادلةٍ تربيعيَّةٍ ممّا يأتي باستعمالِ المُمَيِّز :

a) - x² + 4x - 4 = 0                                          b) 2x² + 8x - 3 = 0                              c) x² - 6x + 11 = 0

الحل : 

صيغةُ المُمَيِّزِ	Δ = b2 - 4ac
بتعويضِ a = - 1 , b = 4  , c = - 4	Δ = (4)2 - 4(-1)(-4)
بالتبسيطِ	Δ = 0

بما أنَّ Δ = 0 ، إذنْ للمُعادلةِ حلٌّ حقيقيٌّ واحدٌ.

---

  b) 2x² + 8x - 3 = 0 

صيغةُ المُمَيِّزِ	Δ = b2 - 4ac
بتعويضِ a = 2 , b = 8  , c = - 3	Δ = (8)2 - 4(2)(-3)
بالتبسيطِ	Δ = 86

بما أنَّ Δ > 0 ، إذنْ للمُعادلةِ حلّانِ حقيقيّانِ مختلفانِ.

---

c) x² - 6x + 11 = 0

صيغةُ المُمَيِّزِ	Δ = b2 - 4ac
بتعويضِ a = 1 , b = -6  , c = 11	Δ = (-6 )2 - 4(1)(11)
بالتبسيطِ	Δ = - 8

بما أنَّ Δ < 0 ، إذنْ ليسَ للمُعادلةِ أيُّ حلٍّ حقيقيٍّ.

---

أتحقق من فهمي صفحة 140

أَحُلُّ كلَّ مُعادلةٍ ممّا يأتي باستعمالِ أيِّ طريقةٍ، مُبَرِّرًا سببَ اختيارِ الطريقةِ :

a) x² + 3x - 28 = 0                                            b) –x² - 10x = 11                                  c) 3x² - 13x = 5

الحل : 

a) x² + 3x - 28 = 0 

يمكنُ تحليلُ الطرفِ الأيسرِ مِنَ المُعادلةِ بسهولةٍ؛ لِذا أَحُلُّها باستعمالِ التحليلِ إلى العواملِ

$x^2+3x-28=0$

$(x-4)(x+7)=0$

$x-4=0 or x+7=0$

$x=4 or x=-7$

إذن جذرا المعادلة  : 4 ، 7 -

---

  b) –x² - 10x = 11     

بما أنَّ معاملَ x² يُساوي 1- ، ومعاملَ x عددٌ زوجيٌّ، فَمِنَ الأفضلِ استعمالُ طريقةِ إكمالِ المُرَبَّعِ.

$-x^2-10x=11$

$x^2+10x+25=-11+25$

${(x+5)}^2=14$

$x+5=\pm \sqrt[]{14}$

$x=-5\pm \sqrt[]{14}$

$x=-5+\sqrt[]{14} or x=-5-\sqrt[]{14}$

$x\approx -1.3 or x\approx -8.7$

إذن جذرا المعادلة  : 8.7 - ، 1.3 -

---

c) 3x² - 13x = 5

بما أنَّهُ لا يمكن تحليل المُعادلة والأعداد فيها كبيرة، فأستعمل القانون العامَّ.

• أستعمل المُمَيّز لتحديد عدد الحُلول الحقيقيَّة للمُعادلة.

$\Delta =b^2-4ac={(-13)}^2-4\left(3\right)(-5)=169+60=229$

بما أنَّ Δ > 0 ، إذنْ للمُعادلةِ حلّانِ حقيقيّانِ مختلفانِ.

• أُطبّقُ القانون العامّ.

صيغة القانون العامّ	$x=\frac{-b\pm \sqrt[]{b^2-4ac}}{2a}$
بتعويض  $a = 3 , b = -13 , c = -5$	$x=\frac{-(-13)\pm \sqrt[]{{(-13)}^2-4\left(3\right)(-5)}}{2\left(3\right)}$
بالتبسيطِ	$x=\frac{13\pm \sqrt[]{229}}{6}$
بفصل الحلين	$x=\frac{13+\sqrt[]{229}}{6} or x=\frac{13-\sqrt[]{229}}{6}$
باستخدام الآلة الحاسبة	$x\approx 4.7 or x\approx 0.4$

أتحقق من فهمي صفحة 143

في مناورة تدريبية للقوات المسلحة الأردنية - الجيش العربي، أٌطلقت قذيفة من ارتفاع 2m ، فمثّل الاقتران $h\left(x\right)=-0.001x^2+0.9x+2$ ارتقفاعها بالمتر عن سطح الأرض؛ حيثُ x المسافة الأفقية بين القذيفة وموقع إطلاقها. أجد المسافة الأفقية بين موقع إطلاق القذيفة وموقع سقوطها.

الحل:

$909.2m$

---

أسئلة أتدرب وأحل المسائل

أَحُلُّ كُلًّ مِنَ المُعادلاتِ الآتيةِ بالقانونِ العامِّ، مُقَرِّبًا إجابتي لأقربِ جُزءٍ مِنْ عشرَةٍ (إنْ لَزِمَ) :

1) 2x² + x - 8 = 0                                                2) 3x² + 5x + 1 = 0                                        3) x² - x - 10 = 0

4) 4x² + 3 = -9x                                                 5) 6x² + 22x + 19 = 0                                   6) x² + 3x = 6

7) 3x² + 1 = 7x                                                   8) 2x² + 11x + 4 = 0                                      9) 4x² + 5x = 3

10) 4x² = 9x - 4                                                11) 7x² = 2 - 3x                                            12) 5x² - 10x + 1 = 0

الحل :

صيغة القانون العام  $x=\frac{-b\pm \sqrt[]{b^2-4ac}}{2a}$ 

1) 2x² + x - 8 = 0   

$x=\frac{-\left(1\right)\pm \sqrt[]{{\left(1\right)}^2-4\left(2\right)(-8)}}{2\left(2\right)}=\frac{ -1\pm \sqrt[]{65}}{4}$

$x=\frac{ -1+\sqrt[]{65}}{4} or x=\frac{ -1-\sqrt[]{65}}{4}$

$x\approx 1.8 or x\approx -2.3$

---

2) 3x² + 5x + 1 = 0 

$x=\frac{-\left(5\right)\pm \sqrt[]{{\left(5\right)}^2-4\left(3\right)\left(1\right)}}{2\left(3\right)}=\frac{ -5\pm \sqrt[]{13}}{6}$

$x=\frac{ -5+\sqrt[]{13}}{6} or x=\frac{ -5-\sqrt[]{13}}{6}$

$x\approx -1.4 or x\approx -0.2$

---

  3) x² - x - 10 = 0 

$x=\frac{-(-1)\pm \sqrt[]{{(-1)}^2-4\left(1\right)(-10)}}{2\left(1\right)}=\frac{1\pm \sqrt[]{41}}{2}$

$x=\frac{ 1+\sqrt[]{41}}{2} or x=\frac{1-\sqrt[]{41}}{2}$

$x\approx 3.7 or x\approx -2.7$

---

4) 4x² + 3 = -9x    $\Rightarrow$ 4x² +9x + 3 = 0  

$x=\frac{-\left(9\right)\pm \sqrt[]{{\left(9\right)}^2-4\left(4\right)\left(3\right)}}{2\left(4\right)}=\frac{-9\pm \sqrt[]{33}}{8}$

$x=\frac{-9+\sqrt[]{33}}{8} or x=\frac{-9-\sqrt[]{33}}{8}$

$x\approx -0.4 or x\approx -1.8$

---

 5) 6x² + 22x + 19 = 0   

$x=\frac{-\left(22\right)\pm \sqrt[]{{\left(22\right)}^2-4\left(6\right)\left(19\right)}}{2\left(6\right)}=\frac{-22\pm \sqrt[]{28}}{12}$

$x=\frac{-22+\sqrt[]{28}}{12} or x=\frac{-22-\sqrt[]{28}}{12}$

$x\approx -1.4 or x\approx -2.3$

---

6) x² + 3x = 6  $\Rightarrow$ x² + 3x - 6 = 0 

$x=\frac{-\left(3\right)\pm \sqrt[]{{\left(3\right)}^2-4\left(1\right)(-6)}}{2\left(1\right)}=\frac{-3\pm \sqrt[]{33}}{2}$

$x=\frac{-3+\sqrt[]{33}}{2} or x=\frac{-3-\sqrt[]{33}}{2}$

$x\approx 1.4 or x\approx -4.4$

---

7) 3x² + 1 = 7x   $\Rightarrow$3x² - 7x + 1 = 0

$x=\frac{-(-7)\pm \sqrt[]{{(-7)}^2-4\left(3\right)\left(1\right)}}{2\left(3\right)}=\frac{ 7\pm \sqrt[]{37}}{6}$

$x=\frac{7+\sqrt[]{37}}{6} or x=\frac{ 7-\sqrt[]{37}}{6}$

$x\approx 2.2 or x\approx 0.2$

---

8) 2x² + 11x + 4 = 0   

$x=\frac{-\left(11\right)\pm \sqrt[]{{\left(11\right)}^2-4\left(2\right)\left(4\right)}}{2\left(2\right)}=\frac{-11\pm \sqrt[]{89}}{4}$

$x=\frac{-11+\sqrt[]{89}}{4} or x=\frac{-11-\sqrt[]{89}}{4}$

$x\approx -0.4 or x\approx -5.1$

---

9) 4x² + 5x = 3  $\Rightarrow$ 4x² + 5x -3 = 0

$x=\frac{-\left(5\right)\pm \sqrt[]{{\left(5\right)}^2-4\left(4\right)(-3)}}{2\left(4\right)}=\frac{-5\pm \sqrt[]{73}}{8}$

$x=\frac{-5+\sqrt[]{73}}{8} or x=\frac{-5-\sqrt[]{73}}{8}$

$x\approx 0.4 or x\approx -1.7$

---

10) 4x² = 9x - 4  $\Rightarrow$ 4x²- 9x + 4 = 0

$x=\frac{-(-9)\pm \sqrt[]{{(-9)}^2-4\left(4\right)\left(4\right)}}{2\left(4\right)}=\frac{9\pm \sqrt[]{17}}{8}$

$x=\frac{ 9+\sqrt[]{17}}{8} or x=\frac{9-\sqrt[]{17}}{8}$

$x\approx 1.6 or x\approx 0.6$

---

11) 7x² = 2 - 3x   $\Rightarrow$  7x² + 3x - 2 = 0  

$x=\frac{-\left(3\right)\pm \sqrt[]{{\left(3\right)}^2-4\left(7\right)(-2)}}{2\left(7\right)}=\frac{-3\pm \sqrt[]{65}}{14}$

$x=\frac{- 3+\sqrt[]{65}}{14} or x=\frac{-3-\sqrt[]{65}}{14}$

$x \approx 0.4 or x\approx -0.8$

---

  12) 5x² - 10x + 1 = 0

$x=\frac{-(-10)\pm \sqrt[]{{(-10)}^2-4\left(5\right)\left(1\right)}}{2\left(5\right)}=\frac{10\pm \sqrt[]{55}}{10}$

$x=\frac{10+\sqrt[]{55}}{10} or x=\frac{10-\sqrt[]{55}}{10}$

$x\approx 1.8 or x\approx 0.1$

---

 

أُحَدِّدُ عددَ الحُلولِ الحقيقيَّةِ لكلِّ مُعادلةٍ تربيعيَّةٍ ممّا يأتي باستعمالِ المُمَيِّز :

13) x² - 6x + 10 = 0                                       14) 2x² - 12x = -18                                15) -5x² + 8x + 9 = 0

الحل : 

13) x² - 6x + 10 = 0 

صيغةُ المُمَيِّزِ	Δ = b2 - 4ac
بتعويضِ a = 1 , b = -6  , c = 10	Δ = (-6)2 - 4(1)(10)
بالتبسيطِ	Δ = - 4

بما أنَّ Δ < 0 ، ، إذنْ ليسَ للمُعادلةِ أيُّ حلٍّ حقيقيٍّ. 

---

14) 2x² - 12x = -18   $\Rightarrow$ 2x² - 12x + 18 = 0

صيغةُ المُمَيِّزِ	Δ = b2 - 4ac
بتعويضِ a = 2 , b = -12  , c = 18	Δ = (-12)2 - 4(2)(18)
بالتبسيطِ	Δ = 0

بما أنَّ Δ = 0 ، إذنْ للمُعادلةِ حلٌّ حقيقيٌّ واحدٌ.

---

  15) -5x² + 8x + 9 = 0 

صيغةُ المُمَيِّزِ	Δ = b2 - 4ac
بتعويضِ a = -5 , b = 8  , c = 9	Δ = (8)2 - 4(-5)(9)
بالتبسيطِ	Δ = 244

بما أنَّ Δ > 0 ، إذنْ للمُعادلةِ حلّانِ حقيقيّانِ مختلفانِ.

---

أَحُلُّ كلَّ مُعادلةٍ ممّا يأتي باستعمالِ أيِّ طريقةٍ، مُبَرِّرًا سببَ اختيارِ الطريقةِ :

16) x² + 4x = 15                                         17) 9x² - 49 = 0                                     18) x² + 4x - 60 = 0

الحل : 

 

16) x² + 4x = 15      

بما أنَّ معاملَ x² يُساوي 1 ، ومعاملَ x عددٌ زوجيٌّ، فَمِنَ الأفضلِ استعمالُ طريقةِ إكمالِ المُرَبَّعِ.

$x^2+4x=15$

$x^2+4x+4=15+4$

${(x+2)}^2=19$

$x+2=\pm \sqrt[]{19}$

$x=-2\pm \sqrt[]{19}$

$x=-2+\sqrt[]{19 }or x=-2-\sqrt[]{19}$

---

 17) 9x² - 49 = 0   

يمكنُ تحليلُ الطرفِ الأيسرِ مِنَ المُعادلةِ بسهولةٍ؛ لِذا أَحُلُّها باستعمالِ التحليلِ إلى العواملِ

$9x^2-49=0$

$(3x-7)(3x+7)=0$

$3x-7=0 or 3x+7=0$

$x=\frac{7}{3} or x=-\frac{7}{3}$

---

18) $x^2 + 4x - 60 = 0$

يمكنُ تحليلُ الطرفِ الأيسرِ مِنَ المُعادلةِ بسهولةٍ؛ لِذا أَحُلُّها باستعمالِ التحليلِ إلى العواملِ 

 $x^2+4x-60=0$

$(x+10)(x-6)=0$

$x+10=0 or x-6=0$

$x=-10 or x=6$

 

19) صناعةٌ : تجري صناعةُ صندوقٍ معدنيٍّ مِنْ صفيحةٍ مُرَبَّعَةِ الشَّكلِ بقطعِ 4 مُرَبَّعاتٍ متطابقةٍ مِنْ زوايا الصَّفيحةِ، طولُ ضلعِ كلِّ مُرَبَّعٍ منها $2 m$ ، ثمَّ تُطوى الجوانبُ لتشكيلِ الصُّندوقِ. إذا كانَ حجمُ الصُّندوقِ $144 m^3$ ، فَأَجِدُ أبعادَ الصفيحةِ الأصليَّةِ التي صُنِعَ منها الصّندوقُ، مُقَرِّبًا إجابتي لأقربِ جُزءٍ مِنْ عشرَةٍ.

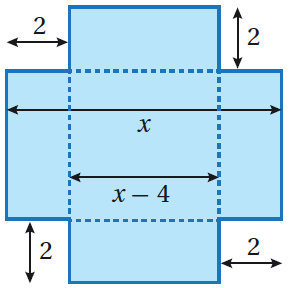الحل : 

حجم الصندوق = الطول $\times$ العرض $\times$ الارتفاع 

$(x-4)(x-4)\left(2\right)=144$

$x^2-8x+16=72$

$x^2-8x-56=0$

أحل المعادلة باستخدام القانون العام 

$x=\frac{-(-8)\pm \sqrt[]{{(-8)}^2-4\left(1\right)(-56)}}{2\left(1\right)}=\frac{8\pm \sqrt[]{324}}{2}$

$x=\frac{8+\sqrt[]{324}}{2} or x=\frac{8-\sqrt[]{324}}{2}$

$x\approx 12.5 or x\approx -4.5$

يُهمل الحل السالب ، إذن  $x \approx 12.5 m$

أبعاد الصفيحة $8.5m , 8.5m , 2m$ مُقربًا كل من الطول والعرض لأقرب جزء من العشرة. 

---

20) حديقةٌ : حديقةٌ مستطيلةُ الشكلِ يزيدُ طولُها على عرضِها بمقدارِ  $5 m$ . إذا كانَتْ مساحتُها  $60 m^2$ ، فَأَجِدُ أبعادَها، مُقَرِّبًا إجابتي لأقربِ جُزءٍ مِنْ مِئَةٍ.

الحل : 

أفرض عرض المستطيل x ، إذن طولها x + 5

مساحة المستطيل = الطول $\times$العرض 

$x(x+5)=60\Rightarrow x^2+5x-60=0$

أحل المعادلة باستخدام القانون العام 

$x=\frac{-\left(5\right)\pm \sqrt[]{{\left(5\right)}^2-4\left(1\right)(-60)}}{2\left(1\right)}=\frac{-5\pm \sqrt[]{265}}{2}$

$x=\frac{-5+\sqrt[]{265}}{2} or x=\frac{-5-\sqrt[]{265}}{2}$

$x\approx 5.64 or x\approx -10.64$

يُهمل الحل السالب ، إذن $x \approx 5.64 m$  

أبعاد الحديقة : العرض $x \approx 5.64 m$ ، الطول $x + 5 \approx 10.64 m$

---

21) هندسةٌ : يُبَيِّنُ الشكلُ الآتي مُثَلَّثًا مساحتُهُ $10 c{m}^2$ . أَجِدُ قيمةَ x ، مُقَرِّبًا إجابتي لأقربِ جُزءٍ مِنْ عشرَةٍ.

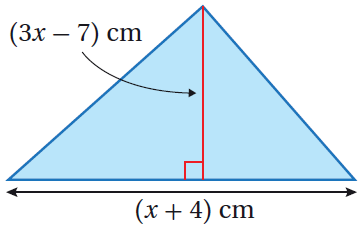
الحل : 

$\frac{1}{2}(x+4)(3x-7)=10$

$(x+4)(3x-7)=20$

$3x^2+5x-28=20$

$3x^2+5x-48=0$

أحل المعادلة باستخدام القانون العام 

$x=\frac{-\left(5\right)\pm \sqrt[]{{\left(5\right)}^2-4\left(3\right)(-48)}}{2\left(3\right)}=\frac{-5\pm \sqrt[]{601}}{6}$

$x=\frac{-5+\sqrt[]{601}}{6} or x=\frac{-5-\sqrt[]{601}}{6}$

$x\approx 3.3 or x\approx -4.9$

يُهمل الحل السالب ، إذن x = 3.3 

---

22) أَحُلُّ المسألةَ الواردةَ في بدايةِ الدرسِ.

مسألةُ اليومِ : في لعبةِ رميِ القرص، رمى لاعب القرص فَمَثَّل الاقتران f(x) = -0.04x2 + 0.84x + 2 ارتفاع القرص بالمتر عن سطح الأرض، حيث x المسافة الأُفقيّة بالمتر بين اللاعب والقرص. أَجدُ المسافة الأُفقيّة بين اللاعب والقرص عندما يصلُ القرصُ إلى سطح الأرض.

الحل : 

أستعملُ القانونَ العامَّ لحلِّ المُعادلةِ:

المُعادلةُ المُرتبطةُ بالاقترانِ	-0.04x2 + 0.84x + 2 =0
صيغةُ القانونِ العامِّ	$x=\frac{-b\pm \sqrt[]{b^2-4ac}}{2a}$
بتعويضِ $a=-0.04,b=0.84,c=2$	$x=\frac{-0.48 \pm \sqrt[]{{(0.48)}^2-4(-0.04)\left(2\right)}}{2(-0.04)}$
بالتبسيط	$x=\frac{-0.48 \pm \sqrt[]{0.2304 +0.32}}{-0.08}$
بفصل الحلين	$x=\frac{-0.48+\sqrt[]{0.5504}}{-0.08} or x=\frac{-0.48 -\sqrt[]{0.5504}}{-0.08}$
باستخدام الآلة الحاسبة	$x\approx -3.25 or x\approx 15.25$

مهاراتُ التفكيرِ العُليا

 

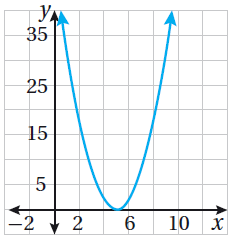
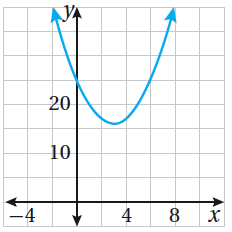
تبريرٌ : أَصِلُ كلَّ مُعادلةٍ في ما يأتي بالتمثيلِ البيانِيِّ للاقترانِ المُرتبطِ بها، مُبَرِّرًا إجابتي :

                                                                 

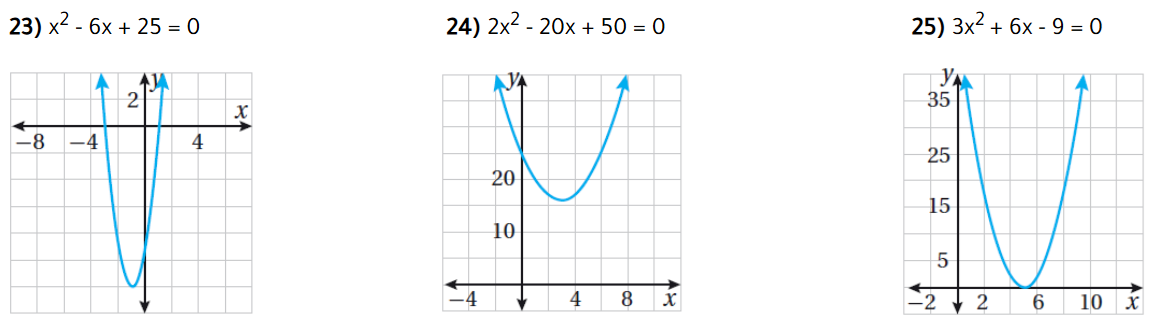
الحل : 

25) 3x2 + 6x - 9 = 0	24) 2x2 - 20x + 50 = 0	23) x2 - 6x + 25 = 0

 

 

 

 

 

 

 

---

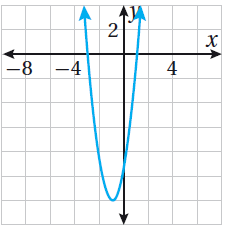26) تَحَدٍّ : حَلَّتْ رنيمُ مُعادلةً تربيعيَّةً باستعمالِ القانونِ العامِّ فكانَتْ إجابتُها $x=\frac{3\pm \sqrt[]{37}}{2}$ . أَجِدُ المُعادلةَ التربيعيَّةَ التي حلَّتها رنيمُ.  
الحل :  

بالمقارنة مع القانون العام لحل المعادلة التربيعية    $x=\frac{-b\pm \sqrt[]{b^2-4ac}}{2a}$

أجد أنّ   b = - 3  ،  a = 1 

أجد c من المميز   Δ = b² - 4ac

$b^2-4ac=37$

${(-3)}^2- 4\times 1\times c=37$

$9-4c=37$

$-4c=28\to c=-7$

إذن المعادلة هي : $x^2-3x-7=0$

---

27) أكتشِفُ الخطأَ : يقولُ نورٌ إنَّ مُمَيِّزَ المُعادلةِ 0 = 2x² + 5x - 1 هُوَ 17 . أكتشِفُ الخطأَ الذي وقعَ فيهِ نورٌ وَأُصَحِّحُهُ.

الحل :  

أخطأ نور بالعمليات الحسابية ؛ إذ حاصل ضرب عدد سالب بعدد سالب ينتج عدد موجب 

والحل الصحيح : 

$\Delta =b^2-4ac=5^2-4\left(2\right)(-1)=25+8=33$

---

أسئلة كتاب التمارين 

أَحُلُّ المُعادلات الآتية بالقانون العامّ، مُقَرِّبًا إجابتي لأقرب جُزء من عشرة (إن لَزِم) :

1) x² + 3x - 3 = 0                                               2) x² - 43x = -6                                             3) 4x² - 20x = -25

4) 5x + 6 - x² = 0                                             5) -6x - x² = 9                                                6) -2x² + 3x = - 4

7) 3x² - 5 + 14x = 0                                          8) 2x² - 5x = 11                                               9) 7 - 4x² = 16x

الحل :  

1) x² + 3x - 3 = 0   

$x=\frac{-\left(3\right)\pm \sqrt[]{{\left(3\right)}^2-4\left(1\right)(-3)}}{2\left(1\right)}=\frac{-3\pm \sqrt[]{21}}{2}$

$x=\frac{-3+\sqrt[]{21}}{2} or x=\frac{-3-\sqrt[]{21}}{2}$

$x\approx 0.8 or x\approx -3.8$

---

    2) x² - 43x = -6  $\Rightarrow$ x² - 43x + 6 = 0

$x=\frac{-(-43)\pm \sqrt[]{{(-43)}^2-4\left(1\right)\left(6\right)}}{2\left(1\right)}=\frac{43\pm \sqrt[]{1825}}{2}$

$x=\frac{43+\sqrt[]{1825}}{2} or x=\frac{43-\sqrt[]{1825}}{2}$

$x\approx 42.9 or x\approx 0.1$

---

 3) 4x² - 20x = -25  $\Rightarrow$  4x² - 20x +25 = 0 

$x=\frac{-(-20)\pm \sqrt[]{{(-20)}^2-4\left(4\right)\left(25\right)}}{2\left(4\right)}=\frac{20\pm \sqrt[]{0}}{8}$

$x=\frac{20}{8}=2.5$

---

4) 5x + 6 - x² = 0     $\Rightarrow$ $-x^2 +5x + 6 = 0$  

$x=\frac{-\left(5\right)\pm \sqrt[]{{\left(5\right)}^2-4(-1)\left(6\right)}}{2(-1)}=\frac{-5\pm \sqrt[]{49}}{-2}=\frac{-5\pm 7}{-2}$

$x=\frac{-5+7}{-2} or x=\frac{-5-7}{-2}$

$x=-1 or x=6$

---

 5) -6x - x² = 9   $\Rightarrow$ $-x^2-6x-9 = 0$

$x=\frac{-(-6)\pm \sqrt[]{{(-6)}^2-4(-1)(-9)}}{2(-1)}$

$x=\frac{6\pm \sqrt[]{0}}{-2}=\frac{6}{-2}=-3$

---

  6) -2x² + 3x = - 4  $\Rightarrow$ $-2x^2 + 3x + 4 = 0$

$x=\frac{-\left(3\right)\pm \sqrt[]{{\left(3\right)}^2-4(-2)\left(4\right)}}{2(-2)}=\frac{-3\pm \sqrt[]{41}}{-4}$

$x=\frac{-3+\sqrt[]{41}}{-4} or x=\frac{-3-\sqrt[]{41}}{-4}$

$x\approx -0.85 or x\approx 2.35$

---

7) 3x² - 5 + 14x = 0   $\Rightarrow$  $3x^2 + 14x - 5 = 0$

$x=\frac{-\left(14\right)\pm \sqrt[]{{\left(14\right)}^2-4\left(3\right)(-5)}}{2\left(3\right)}=\frac{-14\pm \sqrt[]{256}}{6}$

$x=\frac{-14+16}{6} or x=\frac{-14-16}{6}$

$x=\frac{1}{3} or x=-5$

---

8) 2x² - 5x = 11   $\Rightarrow$ $2x^2 - 5x -11= 0$

$x=\frac{-(-5)\pm \sqrt[]{{(-5)}^2-4\left(2\right)(-11)}}{2\left(2\right)}=\frac{5\pm \sqrt[]{113}}{4}$

$x=\frac{5+\sqrt[]{113} }{4} or x=\frac{5-\sqrt[]{113}}{4}$

$x\approx 3.9 or x\approx -1.4$

---

9) 7 - 4x² = 16x  $\Rightarrow$ $-4x^2-16x+7 =0$

$x=\frac{-(-16)\pm \sqrt[]{{(-16)}^2-4(-4)\left(7\right)}}{2(-4)}=\frac{16\pm \sqrt[]{368} }{-8}$

$x=\frac{16+\sqrt[]{368} }{-8} or x=\frac{16-\sqrt[]{368} }{-8}$

$x\approx -4.4 or x\approx 0.4$

---

 

أَحُلُّ كلَّ مُعادلةٍ ممّا يأتي باستعمال أيِّ طريقةٍ، مُبَرِّرًا سبب اختيار الطريقة :

10) x² + 3x + 2 = 2                                     11) x² - 9 = 0                                                     12) x² - 5x - 7 = 0

13) x² - 6x = 0                                           14) (x - 4)² = 13                                                 15) x² + 10x = 1

الحل :  

10) x² + 3x + 2 = 2 $\Rightarrow x^2+3x = 0$

يمكنُ تحليلُ الطرفِ الأيسرِ مِنَ المُعادلةِ بسهولةٍ؛ لِذا أَحُلُّها باستعمالِ التحليلِ إلى العواملِ 

 $x^2+3x=0$

$x(x+3)=0$

$x=0 or x=-3$

---

 11) x² - 9 = 0   

يمكنُ تحليلُ الطرفِ الأيسرِ مِنَ المُعادلةِ بسهولةٍ؛ لِذا أَحُلُّها باستعمالِ التحليلِ إلى العواملِ 

$x^2-9=0$

$(x-3)(x+3)=0$

$x=3 or x=-3$

---

 12) x² - 5x - 7 = 0 

بما أنَّهُ لا يمكن تحليل المُعادلة ومعامل x فردي ، فأستعمل القانون العامَّ.

$x=\frac{-(-5)\pm \sqrt[]{{(-5)}^2-4\left(1\right)(-7)}}{2\left(1\right)}=\frac{5\pm \sqrt[]{53}}{2}$

$x=\frac{5+\sqrt[]{53} }{2} or x=\frac{5-\sqrt[]{53}}{2}$

$x\approx 6.15 or x\approx -1.15$

---

13) x² - 6x = 0   

يمكنُ تحليلُ الطرفِ الأيسرِ مِنَ المُعادلةِ بسهولةٍ؛ لِذا أَحُلُّها باستعمالِ التحليلِ إلى العواملِ 

$x^2-6x=0$

$x(x-6)=0$

$x=0 or x=6$

---

 14) (x - 4)² = 13 

أستخدم طريقة الجذور التربيعية لأنّ المعادلة على الصورة${(x + a)}^2 = c$ حيث $c \ge 0$

$$\begin{gathered} {(x - 4)}^2 = 13 x - 4 = \pm \sqrt{13} \\ x = 4 \pm \sqrt{13} \\ x = 4 + \sqrt{13} or x = 4 - \sqrt{13} \end{gathered}$$

---

15) $x^2 + 10x = 1$

بما أنَّ معاملَ x² يُساوي 1 ، ومعاملَ x عددٌ زوجيٌّ، فَمِنَ الأفضلِ استعمالُ طريقةِ إكمالِ المُرَبَّعِ.

$x^2+10x=1$

$x^2+10x+25=1+25$

${(x+5)}^2=26x+5=\pm \sqrt[]{26}$

$x=-5\pm \sqrt[]{26}$

$x=-5+\sqrt[]{26} or x=-5-\sqrt[]{26}$

---

16) أرضيّاتٌ : أرضيَّةٌ على شكلِ مُتوازي أضلاعٍ طولُ قاعدتِهِ $(5x-2) m$ ، وارتفاعُهُ $(3x+1) m$ . إذا كانَتْ مساحةُ الأرضيَّةِ $130 m^2$ ، فما طولُ قاعدةِ المُتوازي وما ارتفاعُهُ؟

الحل :  

مساحة متوازي الأضلاع  = طول القاعدة $\times$ الأرتفاع 

$$\begin{gathered} (5x - 2)(3x + 1) = 130 \\ 15x^2-x - 132 = 0 \end{gathered}$$

أستخدم القانون العام لحل المعادلة التربيعية : 

$x=\frac{-(-1)\pm \sqrt[]{{(-1)}^2-4\left(15\right)(-132)}}{2\left(15\right)}=\frac{1\pm \sqrt[]{7921}}{30}$

$x=\frac{1+89}{30} or x=\frac{1-89}{30}$

$x\approx 3 or x\approx -2.9$

يُهمل الحل السالب، إذن x = 3 

طول القاعدة 5x - 2، إذن طول القاعدة $13 m$، الارتفاع 3x + 1، إذن الارتفاع $10 m$

---

أستعملُ المساحة المُعطاة في كلٍّ ممّا يأتي لأجِدَ قيمة x ، مُقَرِّبًا إجابتي لأقربِ جُزءٍ من عشرَة :

17) A = 150 cm²                                                                       18) A = 45 cm²

                                           

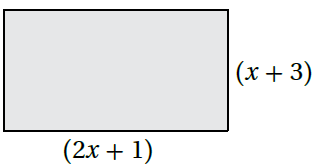
الحل : 

17) A = 150 cm²   

$(2x+1)(x+3)=150$

$2x^2+7x+3=150$

$2x^2+7x-147=0$

$x=\frac{-\left(7\right)\pm \sqrt[]{{\left(7\right)}^2-4\left(2\right)(-147)}}{2\left(2\right)}=\frac{-7\pm \sqrt[]{1225}}{4}=\frac{-7\pm 35}{4}$

$x=\frac{-7+35}{4} or x=\frac{-7-35}{4}$

$x=7 or x=-10.5$

يُهمل الحل السالب  ، إذن  x = 7

---

 18) A = 45 cm²

 $\frac{1}{2}(4x-1)(x+2)=45$

$4x^2+7x-2=90$

$4x^2+7x-92=0$

$x=\frac{-\left(7\right)\pm \sqrt{{ \left(7\right)}^2-4\left(4\right)(-92)}}{2\left(4\right)}=\frac{-7\pm \sqrt[]{1521}}{8}=\frac{-7\pm 39}{8}$

$x=\frac{-7+39}{8} or x=\frac{-7-39}{8}$

$x=4 or x=-5.75$

يُهمل الحل السالب  ، إذن  x = 4

---

19) أكتشِفُ الخطأَ: حلَّ كريم معادلةً تربيعيةً باستعمالِ القانونِ العامِّ كما هوَ مُبيَّنٌ أدناهُ. أكتشِفُ الخطأَ في حل كريم، وَأُصَحِّحُهُ:

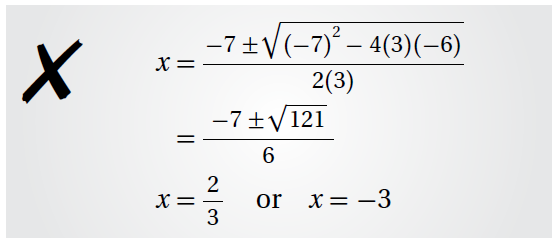
الحل :  

أخطأ كريم بتعويض عن $b=-7$ بالقيمة 7 في القانون العام.

$x=\frac{-(-7)\pm \sqrt[]{{(-7)}^2-4\left(3\right)(-6)}}{2\left(3\right)}=\frac{7\pm \sqrt[]{121}}{6}=\frac{7\pm 11}{6}$

$x=\frac{7+11}{6} or x=\frac{7-11}{6}$

$x=3 or x=-\frac{2}{3}$