حلُّ المُعادلاتِ التربيعيَّةِ باستعمالِ القانونِ العامِّ
Solving Quadratic Equations Using
the Quadratic Formula
فكرة الدرس : حلُّ المُعادلةِ التربيعيَّةِ باستعمال القانون العامِّ.
أولًا : القانونُ العامُّ
|
مفهومٌ أساسيٌّ (حلُّ المُعادلةِ التربيعيَّةِ بالقانونِ العامِّ) يُمكنُ حلُّ المُعادلةِ التربيعيَّةِ بالقانونِ العامِّ على النَّحوِ الآتي :
حيث |
مثال :
أَحُلُّ كُلًّ مِن المُعادلات الآتية بالقانون العامّ، مُقَرِّبًا إجابتي لأقرب جُزءٍ مِن عشرَة (إن لَزم) :
الحل :
الخُطوة 1 : أكتبُ المُعادلةَ بالصورةِ القياسيَّةِ.
| المُعادلةُ المُعطاةُ | |
| بطرح 3 من طَرَفَيِ المُعادلة |
الخُطوةُ 2 : أُطَبِّقُ القانونَ العامَّ.
| صيغةُ القانونِ العامِّ | |
| بتعويضِ | |
| بالتبسيطِ | |
| بالجمعِ، ثمَّ إيجادِ الجذرِ التربيعيِّ | |
| بفصلِ الحلَّيْنِ | |
| بالتبسيط |
إذن جذرا المعادلة هما :
الخُطوة 1 : أكتبُ المُعادلةَ بالصورةِ القياسيَّةِ.
| المُعادلةُ المُعطاةُ | |
| بطرح 3 من طَرَفَيِ المُعادلة |
الخُطوةُ 2 : أُطَبِّقُ القانونَ العامَّ.
| صيغةُ القانونِ العامِّ | |
| بتعويضِ | |
| بالتبسيطِ | |
| بالجمعِ | |
| بفصلِ الحلَّيْنِ | |
| باستخدام الآلة الحاسبة |
إذن جذرا المعادلة التقريبيين هما :
ثانيًا : المُمَيِّز
يمكنُ تحديدُ عددِ الحُلولِ الحقيقيَّةِ للمُعادلةِ التربيعيَّةِ قبلَ حلِّها باستعمالِ المُمَيِّزِ ، وَهُوَ المقدارُ التربيعيُّ الذي يقعُ أسفلَ الجذرِ التربيعيِّ
في القانونِ العامِّ ( b2 - 4ac )، وَيُرمَزُ لَهُ بالرَّمزِ Δ.

مفهومٌ أساسيٌّ (استعمالُ المُمَيِّز)
|
مُمَيِّزُ المُعادلةِ التربيعيَّةِ ax2 + bx + c = 0 هُوَ Δ = b2 - 4ac ، ويمكنُ استعمالُهُ لتحديدِ عددِ حلولِ المُعادلةِ التربيعيَّةِ كما يأتي:
|
مثال :
أُحَدِّدُ عدد الحُلول الحقيقيَّة لكلِّ مُعادلة تربيعيَّة ممّا يأتي باستعمال المُمَيِّز :
| صيغةُ المُمَيِّزِ | Δ = b2 - 4ac |
| بتعويضِ a =1 , b = 2 , c = - 4 | Δ = 22 - 4(1)(-4) |
| بالتبسيطِ | Δ = 20 |
بما أنَّ Δ > 0 ، إذنْ للمُعادلةِ حلّانِ حقيقيّانِ مختلفانِ.
|
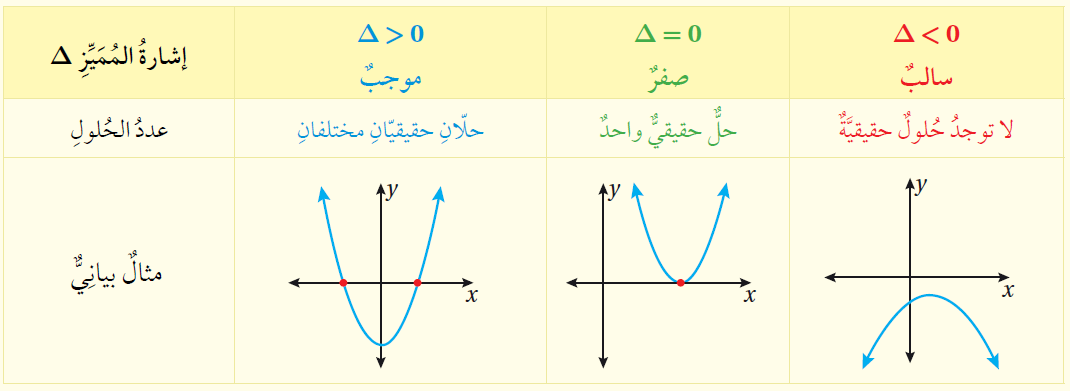
الدّعم البيانِي : يُظهِر التمثيل البيانيُّ المُجاور لمنحنى الاقترانِ التربيعيِّ المُرتبط بالمُعادلة 0 = x2+ 2x - 4 وجود حلَّيْن حقيقيَّيْن مختلفَيْن لها. |
 |
| صيغةُ المُمَيِّزِ | Δ = b2 - 4ac |
| بتعويضِ a =1 , b = -6 , c = 9 | Δ = (-6)2 - 4(1)(9) |
| بالتبسيطِ | Δ = 0 |
بما أنَّ Δ = 0 ، إذنْ للمُعادلةِ حلٌّ حقيقيٌّ واحدٌ.
|
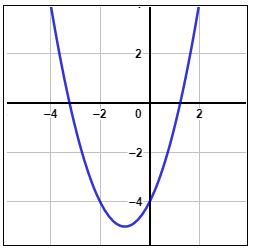
الدَّعمُ البيانِيُّ : يُظهِر التمثيل البيانِيّ المُجاور لمنحنى الاقتران التربيعيِّ المُرتبط بالمُعادلةِ 0 = x2 - 6x + 9 وجود حلٍّ حقيقيٍّ واحد. |
 |
| صيغةُ المُمَيِّزِ | Δ = b2 - 4ac |
| بتعويضِ a =1 , b = -6 , c = 9 | Δ = (-4)2 - 4(1)(5) |
| بالتبسيطِ | Δ = - 4 |
بما أنَّ Δ < 0 ، إذنْ ليسَ للمُعادلةِ أيُّ حلٍّ حقيقيٍّ.
|
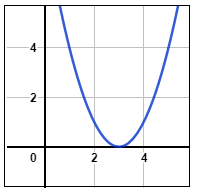
الدَّعمُ البيانِيُّ : يُظهِرُ التمثيل البيانِيُّ المُجاور لمنحنى الاقتران التربيعيِّ المُرتبط بالمُعادلة 0 = x2 - 4 x + 5 عدم وجود أيّ حلّ حقيقيّ للمُعادلة. |
 |
ثالثًا : اختيار الطريقة الأنسب لحلِّ المُعادلة التربيعيّة
تعلَّمتُ خمسَ طرائقَ لحلِّ المُعادلاتِ التربيعيَّةِ، وفي بعضِ الأحيانِ يكونُ استعمالُ إحدى هذهِ الطرائقِ أنسبَ مِنِ استعمالِ الطرائقِ الأُخرى، وَيُبَيِّنُ الجدولُ الآتي ملخَّصًا لهذِهِ الطرائقِ وإيجابياتِ كلٍّ منها وسلبياتِهِ.
ملخَّصُ المفهومِ (طرائقُ حلِّ المُعادلاتِ التربيعيَّةِ)
| الطريقةُ | الإيجابياتُ | السلبياتُ |
| التمثيلُ البياني |
• يمكنُ استعمالُها لحلِّ أيِّ مُعادلةٍ تربيعيَّةٍ. • يمكنُ بسهولةٍ تحديدُ الحُلولِ مِنَ التمثيلِ. |
• قد لا تُعطي حلولً دقيقةً. |
|
التحليلُ إلى العواملِ |
• مِنْ أفضلِ الطرائقِ لتجرِبَتِها أوَّلًا. • تُعطي إجابةً مباشرةً إذا كانَتِ المُعادلةُ قابلةً للتحليلِ أو كانَ الحدُّ الثابتُ صِفرًا. |
• ليستْ جميعُ المُعادلاتِ التربيعيَّةِ قابلةً للتحليلِ. |
| استعمالُ الجُذورِ التربيعيَّةِ |
• تُستعمَلُ لحلِّ المُعادلاتِ على الصورةِ ، حيث |
• لا تُستعمَلُ إذا كانَ الحدُّ bx موجودًا. |
| إكمالُ المُرَبَّعِ |
• يمكنُ استعمالُها لحلِّ أيِّ مُعادلةٍ تربيعيَّةٍ على الصورةِ |
• في بعضِ الأحيانِ تكونُ الحساباتُ مُعَقَّدَةً. |
| القانونُ العامُّ |
• يمكنُ استعمالُها لحلِّ أيِّ مُعادلةٍ تربيعيَّةٍ على الصورةِ |
• قد تستغرقُ وقتًا أطولَ مِنْ باقي الطرائقِ لإجراءِ الحساباتِ. |
مثال :
أَحُلّ كلَّ مُعادلة ممّا يأتي باستعمال أيِّ طريقة ، مُبَرِّرًا سبب اختيار الطريقة :
يمكنُ تحليلُ الطرفِ الأيسرِ مِنَ المُعادلةِ بسهولةٍ؛ لِذا أَحُلُّها باستعمالِ التحليلِ إلى العواملِ
إذن جذرا المعادلة : 5 ، 1 -
بما أنَّ معاملَ x2 يُساوي 1، ومعاملَ x عددٌ زوجيٌّ، فَمِنَ الأفضلِ استعمالُ طريقةِ إكمالِ المُرَبَّعِ.
إذن جذرا المعادلة التقريبيين : 5.3 ، 1.3-
بما أنَّهُ لا يمكن تحليل المُعادلة والأعداد فيها كبيرة، فأستعمل القانون العامَّ.
• أستعمل المُمَيّز لتحديد عدد الحُلول الحقيقيَّة للمُعادلة.
بما أنَّ Δ > 0 ، إذنْ للمُعادلةِ حلّانِ حقيقيّانِ مختلفانِ.
• أُطبّقُ القانون العامّ.
| صيغة القانون العامّ | |
| بتعويض | |
| بالتبسيطِ | |
| بفصل الحلين | |
| باستخدام الآلة الحاسبة |