حلول أسئلة أتحقق من فهمي
حجم الهرم :
2)
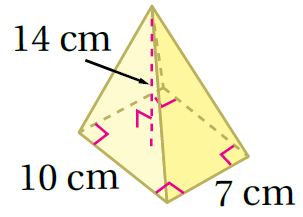
صيغةُ حجمِ الهَرَمِ
القاعدة على شكل مستطيل وبتعويض الأبعاد أَجِدُ الناتجَ
3)
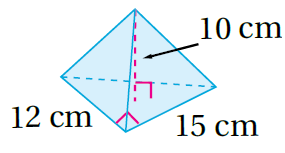
صيغةُ حجمِ الهَرَمِ
القاعدة على شكل مثلث وبتعويض الأبعاد أَجِدُ الناتجَ
أَجِدُ حجمَ أصغرِ هَرَمٍ في المحميّةِ علمًا أنَّ ارتفاعَهُ 18m وَطولَ ضِلعِ قاعدتِهِ المربعةِ 19.5m أقرّبُ إجابتي لِأقربِ جزءٍ مِنْ عشرةٍ.
صيغةُ حجمِ الهَرَمِ
القاعدة مربعة وبتعويض الأبعاد أَجِدُ الناتجَ
حجم المخروط:
2)
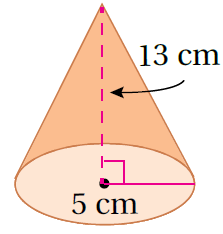
صيغةُ حجمِ المخروطِ
بتعويض الأبعاد أجد الناتج
3)
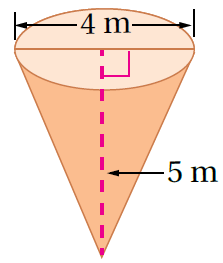
صيغةُ حجمِ المخروطِ
بتعويض الأبعاد أجد الناتج
في المثالِ السابقِ(4) إذا كانَ طولُ نصفِ قُطرِ كَومَةِ مِلْحٍ 35cm ، وَارتفاعُها 40cm أَجِدُ حجمَ الكَومَةِ، وَأقرّبُ إجابتي لِأقربِ جزءٍ مِنْ عشرةٍ.
صيغةُ حجمِ المخروطِ
بتعويض الأبعاد أجد الناتج
حلول أسئلة أتدرب وأحل المسائل
أَجِدُ حجمَ كلِّ مجسّمٍ ممّا يأتي، وَأقرّبُ إجابتي لِأقربِ جزءٍ مِنْ مئةٍ:
1)
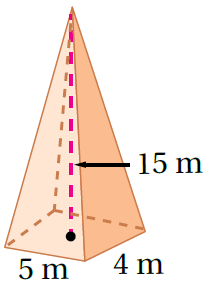
صيغةُ حجمِ الهَرَمِ
القاعدة على شكل مستطيل وبتعويض الأبعاد أَجِدُ الناتجَ
2)
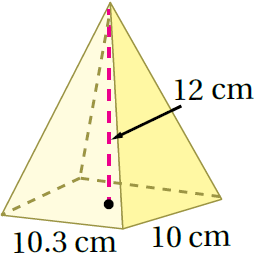
صيغةُ حجمِ الهَرَمِ
القاعدة على شكل مستطيل وبتعويض الأبعاد أَجِدُ الناتجَ
3)
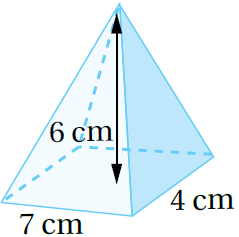
صيغةُ حجمِ الهَرَمِ
القاعدة على شكل مستطيل وبتعويض الأبعاد أَجِدُ الناتجَ
أَجِدُ حجمَ كلِّ مخروطٍ ممّا يأتي، وَأقرّبُ إجابتي لِأقربِ جزءٍ مِنْ عشرةٍ:
4)
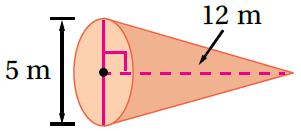
صيغةُ حجمِ المخروطِ
بتعويض الأبعاد أجد الناتج
5)
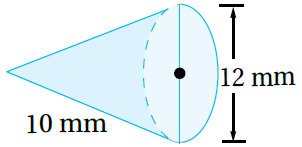
صيغةُ حجمِ المخروطِ
بتعويض الأبعاد أجد الناتج
6)
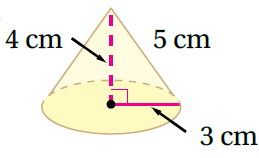
صيغةُ حجمِ المخروطِ
بتعويض الأبعاد أجد الناتج
أَجِدُ حجمَ كلِّ مجسَّمٍ ممّا يأتي، وَأقرّبُ إجابتي لِأقربِ جزءٍ مِنْ عشرةٍ:
7) هَرَمٌ ارتفاعُهُ 5dm وَمساحةُ قاعدتِهِ 18cm2
صيغةُ حجمِ الهرم ، وبتعويض الأبعاد بعد توحيد الوحدات dm=10cm أجد الناتج
8) مخروطٌ طولُ نصفِ قُطرِهِ 4mm وَارتفاعُهُ 6.5mm
صيغةُ حجمِ المخروط، وبتعويض الأبعاد أجد الناتج
9) أكوابٌ: يبيّنُ الشكلُ المجاورُ كوبَينِ، المنطقةُ الداخليةُ في كلٍّ منهُما على شكلِ مخروطٍ. أيُّ الكوبَينِ يتّسعُ لكمّيةٍ أكبرَ مِنَ السائلِ؟ أبرّرُ إجابتي.
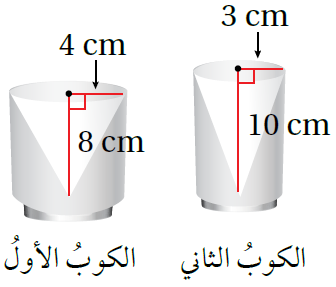
حجم الكوب الأول :
صيغةُ حجمِ المخروط، وبتعويض الأبعاد أجد الناتج
حجم الكوب الثاني :
صيغةُ حجمِ المخروط، وبتعويض الأبعاد أجد الناتج
المخروط الأول يتسع لكمية أكبر من السوائل
أَجِدُ حجمَ كلِّ مجسَّمٍ ممّا يأتي، وَأقرّبُ إجابتي لِأقربِ جزءٍ مِنْ مئةٍ:
10)
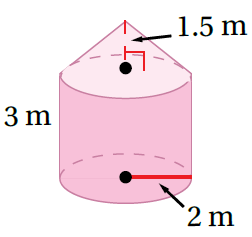
حجم المنشور = حجم المخروط + حجم الأسطوانة
باخذ كعامل مشترك - الاسطوانة والمخروط لهما نفس القطر - وتعويض الأبعاد أجد الناتج
11)
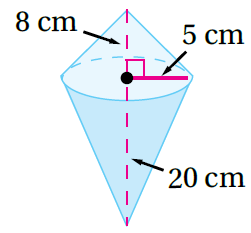
حجم المنشور = حجم المخروط الأول + حجم المخروط الثاني
باخذ كعامل مشترك - لهما نفس القطر - وتعويض الأبعاد أجد الناتج
12)
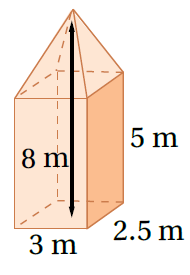
حجم المنشور = حجم الهرم + حجم المنشور الرباعي
بأخذ B كعامل مشترك - لهما نفس القاعدة- وتعويض الأبعاد أجد الناتج
13) علومٌ: يبيّنُ الشكلُ المجاورُ قُمعَينِ يُستخدَمانِ في مختبراتِ العلومِ، القُمعُ(1) على شكلِ مخروطٍ، وَالقُمعُ (2) على شكلِ مخروطٍ مَعَ أُسطوانةٍ متصِلَةِ بقاعدتِهِ.
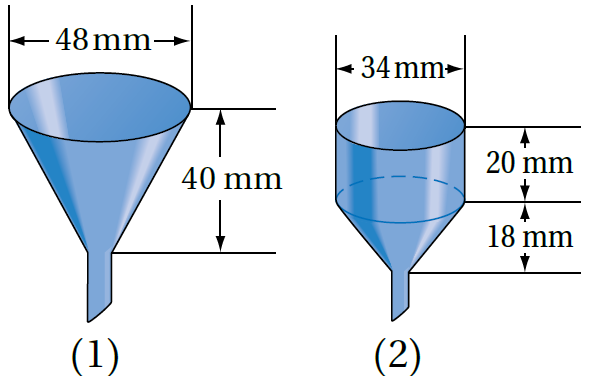
أيُّ القُمعَينِ حجمُهُ أكبرُ؟ أبرّرُ إجابتي.
حجم القمع (1): يساوي حجم المخروط
صيغةُ حجمِ المخروط، وبتعويض الأبعاد أجد الناتج
حجم القمع (2): يساوي حجم المخروط + حجم الأسطوانة
باخذ كعامل مشترك - لهما نفس القطر - وتعويض الأبعاد أجد الناتج
حجم القمع الأول أكبر
أستعملُ المعلوماتِ الموضَّحةَ على كلِّ شكلٍ ممّا يأتي لإيجادِ البُعدِ المفقودِ:
14)
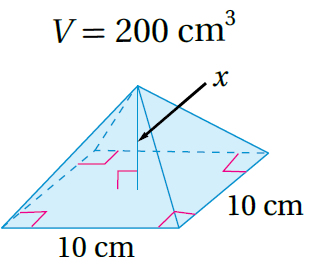
صيغةُ حجمِ الهرم، وبتعويض الأبعاد أجد الارتفاع المفقود x
15)
صيغةُ حجمِ المخروط ، وبتعويض الأبعاد أجد نصف القطر المفقود x
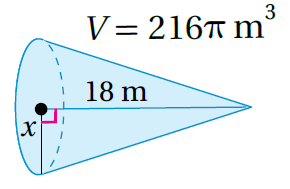
16) أهرامُ مِصرَ: أعودُ إلى فقرةِ (أستكشفُ) بدايةَ الدرسُِ وَأحلُّ المسألةَ.
أجد حجم الهرم :
صيغةُ حجمِ الهرم، وبتعويض الأبعاد أجد الحجم
17) تبريرٌ: يبيّنُ الشكلُ المجاورُ مخروطًا وَأُسطوانةً لَهُما الحجمُ نفسُهُ،
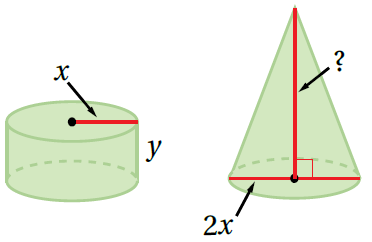
ما علاقةُ ارتفاعِ المخروطِ بِارتفاعِ الأُسطوانةِ؟ أبرّرُ إجابتي.
الشكلين لهما نفس الحجم ، أكتب صيغةُ حجمِ الهرم والمخروط
بتعويض الأبعاد والتبسيط أجد العلاقة بين ارتفاع المخروط وارتفاع الأسطوانة
18) أكتشفُ الخطأَ: أبيّنُ الخطأَ في إيجادِ حجمِ كلِّ مجسَّمٍ مِنَ المجسَّمَينِ الآتيَينِ، وَأصححُهُ.
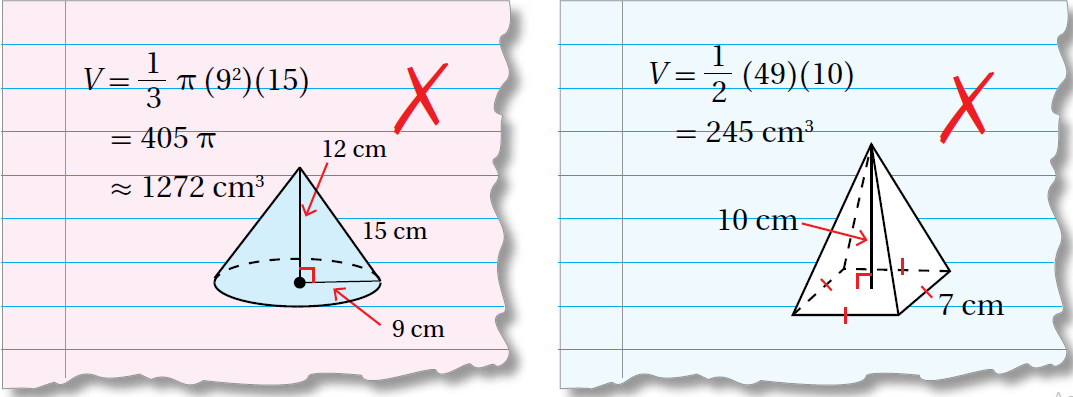
الخطأ في إيجاد حجم المخروط :
الإرتفاع = 12cm وليس 15cm ومنه الحجم الصحيح يساوي 1017.9cm2
الخطأ في إيجاد حجم الهرم :
قانون الحجم يساوي ثلث القاعدة وليس نصفها ومنه الحجم الصحيح يساوي 163.3cm2
19) تبريرٌ: يسقطُ الرّملُ في الساعةِ الرّمليةِ المجاورةِ بِمعدَّلِ 50cm3 لكلِّ دقيقةٍ. كَمْ مِنَ الوقتِ يحتاجُ الرملُ لِيسقطَ كلُّهُ في الجزءِ السفليِّ؟
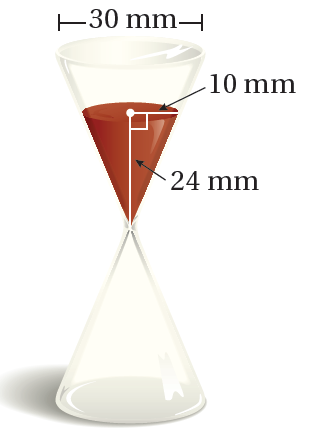
أجد حجم الرمل الموجود في الساعة ، ويساوي حجم المخروط
صيغةُ حجمِ المخروط ، وبتعويض الأبعاد أجد حجم الرمل الموجود في الساعة
بإستخدام معدل التفريغ أجد الوقت اللازم ليسقط جميع الرمل في الجزء السفلي
يجب توحيد الوحدات قبل البدء في الحل (1cm3=1000mm3)
20)أكتبُُ : أصفُ العلاقةَ بينَ حجمِ الهَرَمِ وَحجمِ المنشورِ المساوي لَهُ في القاعدةِ وَالارتفاعِ.
حجم الهرم يساوي ثلث حجم المنشور المساوي له في القاعدة والإرتفاع
حلول أسئلة كتاب التمارين
أَجِدُ حجمَ كلِّ مجسَّمٍ ممّا يأتي، وَأقرّبُ إجابتي لِقربِ جُزءٍ مِنْ عشرةٍ:
1)
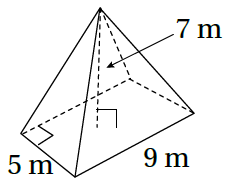
2)
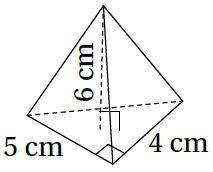
3)
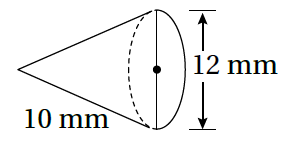
أَجِدُ حجمَ كلِّ مجسَّمٍ ممّا يأتي:
4) هَرَمٌ قاعدتُهُ مربَّعةُ الشكلِ طولُ ضلعِها 22m وَارتفاعُهُ 17m
5) مخروطٌ قُطْرُ قاعدتِهِ 12m وَارتفاعُهُ 5m
6) كريستالٌ: تتكوّنُ قطعةُ الكريستالِ المجاورةُ مِنْ هَرَمَينِ قاعدةُ كلٍّ منهُما مربَّعةُ الشكلِ. أَجِدُ حجمَ قطعةِ الكريستالِ، أقرّبُ إجابتي لِأقربِ جزءٍ مِنْ عشرةٍ.
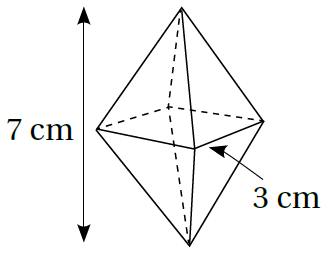
حجم القطعة = مجموع حجم الهرمين (لهما نفس القاعدة)
انتبه : ارتفاع الهرم الثاني
7) هرمٌ قاعدتُهُ مربَّعةُ الشكل،ِ طولُ ضلعِها 6.4cm وَحجمُهُ 81.3cm3 أَجِدُ ارتفاعَ الهَرَمِ.
8) زجاجةٌ: يبيّنُ الشكلُ المجاورُ زجاجةً على شكلِ مَخروطٍ ممتلئةً بِالماءِ، يتسربُ مِنْها الماءُ بِمعدَّلِ 5cm3 في الدقيقةِ. أَجِدُ الوقتَ اللازمَ لِتفرغَ الزجاجةُ مِنَ الماءِ بِالكاملِ.
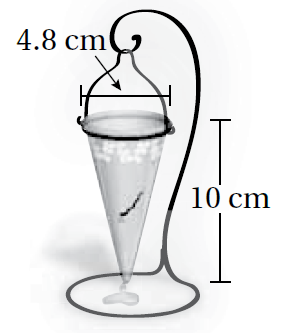
9) عطرٌ: زجاجةُ عطرٍ على شكلِ مَخروطٍ، طولُ قُطرِ قاعدتِها 6.5cm وَارتفاعُها 6m أَجِدُ كمّيّةَ العطرِ الّذي تتّسعُ لَهُ الزجاجةُ.
كمية العطر = حجم المخروط
توحيد الوحدات 6 متر = 600 سانتي متر
10) تبريرٌ: ما كمّيّةُ الزجاجِ اللازمةُ لِتصنيعِ 1000 قطعةٍ مِنْ ثقّالةِ الورقِ المجاورةِ. أبرّرُ إجابتي
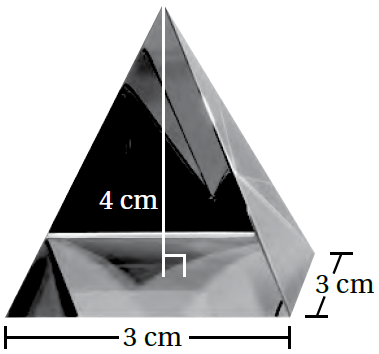
حجم القطعة الواحدة
كمية الزجاج اللازمةُ لِتصنيعِ 1000 قطعةٍ