رياضيات فصل أول

الثامن

الشرح الملخص أوراق العمل حل اسئلة الدرس النتاجات

حالات خاصة من التحليل

أتحقق من فهمي 1 : أحلل كل مما يأتي :

$3) x^{2} - 100 = x^{2} - 10^{2}$

$= (x - 10) (x + 10)$

$4) 100 y^{2} - 36 = {(10 y)}^{2} - 6^{2}$

$= (10 y - 6) (10 y + 6)$

$5) 81 d^{2} - 49 r^{2} = {(9 d)}^{2} - {(7 r)}^{2}$

$= (9 d - 7 r) (9 d + 7 r)$

$6) 64 c^{2} - 1 = {(8 c)}^{2} - 1^{2}$

$= (8 c - 1) (8 c + 1)$

أتحقق من فهمي 1 : أحلل كل مما يأتي :

$4) b^{4} - c^{4} = {(b^{2})}^{2} - {(c^{2})}^{2}$

$= (b^{2} - c^{2}) (b^{2} + c^{2})$

$= (b - c) (b + c) (b^{2} + c^{2})$

$5) 6 w^{3} - 24 w = 6 w (w^{2} - 4)$

$= 6 w (w - 2) (w + 2)$

$6) 4 m^{4} - 9 m^{2} + 8 m^{2} k - 18 k = (4 m^{4} - 9 m^{2}) + (8 m^{2} k - 18 k)$

$= m^{2} (4 m^{2} - 9) + 2 k (4 m^{2} - 9)$

$= (4 m^{2} - 9) (m^{2} + 2 k)$

$= (2 m - 3) (2 m + 3) (m^{2} + 2 k)$

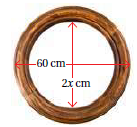أعمالٌ فنيةٌ: صنعَ مرادٌ إطارَ صورةٍ خشبيًّا دائريًّا كما في الشكلِ المجاورِ. أكتبُ مقدارًا جبريًّا يمثلُ مساحةَ الإطارِ الخشبيِّ، ثُمَّ أحللُهُ.

الحل :

مساحة الإطار الخشبي = مساحة الدائرة الكبرى A1 مساحة الدائرة الصغرى A2

حيث : 1- نصف قطر الدائرة الكبرى يساوي 30 .

2- صف قطر الدائرة الصغرى يساوي $x$ .

$A = A 1 - A 2$

$= π ({r_{1})}^{2} - π {(r_{2})}^{2} = π 30^{2} - {πx}^{2}$

$= 900 π - {πx}^{2}$

$= π (900 - x^{2})$

$= π (30 - x) (30 + x)$

أحددُ ما إذا كانَتْ كلُّ ثلاثيّةِ حدودٍ ممّا يأتي تمثلُ مربعًا كاملً أَمْ لا، وإذا كانَتْ تمثلُهُ فأحللُها :

$3) x^{2} - 24 x + 144$

يمكن أن نحدد ثلاثية الحدود التي تمثل مربعاً كاملاً باختبار الحدود الثلاثة كالتالي :

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي $2 * x * 12$ ؟ نعم

إذا الثلاثية تمثل مريعا كاملاً وتمثيلها كالتالي :

$x^{2} - 24 x + 144 = (x - 12) (x - 12)$

$4) 4 x^{2} - 12 x + 9$

يمكن أن نحدد ثلاثية الحدود التي تمثل مربعاً كاملاً باختبار الحدود الثلاثة كالتالي :

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي $2 * 2 x * 3$ ؟ نعم

إذا الثلاثية تمثل مريعا كاملاً وتمثيلها كالتالي :

$4 x^{2} - 12 x + 9 = (2 x - 3) (2 x - 3)$

$5) x^{2} + \frac{2}{5} x + \frac{1}{25}$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي : $2 * x * \frac{1}{5} = \frac{2}{5} x$

إذا الثلاثية تمثل مريعا كاملاً وتمثيلها كالتالي :

$x^{2} + \frac{2}{5} x + \frac{1}{25} = (x + \frac{1}{5}) (x + \frac{1}{5})$

أتدرب وأحل المسائل.

أحللُ كلًّ ممّا يأتي:

$1) u^{2} - 64 = (u - 8) (u + 8)$

$2) \frac{1}{9} x^{2} - \frac{1}{25} = (\frac{1}{3} x - \frac{1}{5}) (\frac{1}{3} x + \frac{1}{5})$

$3) 36 y^{2} - 1 = (6 y - 1) (6 y + 1)$

$4) v^{4} - 625 r^{2} = (v^{2} - 25 r) (v^{2} + 25 r)$

$5) a^{2} - w^{2} z^{2} = (a - w z) (a + w z)$

$6) - 16 y^{2} + 49 = 49 - 16 y^{2}$

$= (7 - 4 y) (7 + 4 y)$

أحللُ كلًّ ممّا يأتي:

$7) a b^{2} - 100 a = a (b^{2} - 100)$

$= a (b - 10) (b + 10)$

$8) x - x^{3} = x (1 - x^{2})$

$= x (1 - x) (1 + x)$

$9) 12 b^{3} + 2 b^{2} - 192 b - 32 = (12 b^{3} + 2 b^{2}) + (- 192 b - 32)$

$= 2 b^{2} (6 b + 1) - 32 (6 b + 1)$

$= (6 b + 1) (2 b^{2} - 32)$

$= (6 b + 1) 2 (b^{2} - 16)$

$= 2 (6 b + 1) (b - 4) (b + 4)$

$10) d^{3} - 5 d^{2} - 100 d + 500 = (d^{3} - 5 d^{2}) + (500 - 100 d)$

$= d^{2} (d - 5) + 100 (5 - d)$

$= d^{2} (d - 5) - 100 (d - 5)$

$= (d - 5) (d^{2} - 100)$

$= (d - 5) (d - 10) (d + 10)$

أحددُ أنَّ كلَّ ثلاثيةِ حدودٍ ممّا يأتي تمثلُ مربعًا كاملً أَمْ لا، وإذا كانَتْ تمثلُهُ فأحللُها:

$11) w^{2} - 18 w + 81$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي $2 * w * 9$ ؟ نعم

إذا الثلاثية تمثل مريعا كاملاً وتمثيلها كالتالي :

$w^{2} - 18 w + 81 = (w - 9) (w - 9) = {(w - 9)}^{2}$

$12) x^{2} + 2 x - 1$

هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ لا ، لأن 1- لا يمكن أن يكون مربع كامل.

ومنه فإن ثلاثية الحدود هنا لا تمثل مربعاً كاملاً

$13) y^{2} + 8 y + 16$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي $2 * y * 4$ ؟ نعم

$y^{2} + 8 y + 16 = (y + 4) (y + 4) = {(y + 4)}^{2}$

$14) 9 x^{2} - 30 x + 10$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ لا ، لأن 10 لا يمثل مربعاً كاملاً .

ومنه فإن ثلاثية الحدود هنا لا تمثل مربعاً كاملاً

أحللُ كلًّ ممّا يأتي:

$15) 3 t^{3} + 24 t^{2} + 48 t = 3 t (t^{2} + 8 t + 16)$

$= 3 t (t + 4) (t + 4) 3 t {(t + 4)}^{2}$

$16) 50 g^{2} + 40 g + 8 = 2 (25 g^{2} + 20 g + 4)$

$= 2 (5 g + 2) (5 g + 2) = 2 {(5 g + 2)}^{2}$

$17) 27 g^{2} - 90 g + 75 = 3 (9 g^{2} - 30 g + 25)$

$= 3 (3 g - 5) (3 g - 5)$

$18) 18 y^{2} - 48 y + 32 = 2 (9 y^{2} - 24 y + 16)$

$= 2 (3 y - 4) (3 y - 4)$

$19) 5 x^{2} - 60 x + 180 = 5 (x^{2} - 12 x + 36)$

$= 5 (x - 6) (x - 6)$

$20) 16 r^{3} - 48 r^{2} + 36 r = 4 r (4 r^{2} - 12 r + 9)$

$= 4 r (2 r - 3) (2 r - 3)$

$21) 12 x^{2} - 84 x + 147 = 3 (4 x^{2} - 28 x + 49)$

$= 3 (2 x - 7) (2 x - 7)$

$22) 4 x^{2} - 80 x + 400 = 4 (x^{2} - 20 x + 100)$

$= 4 (x - 10) (x - 10)$

23) نحاسٌ: يبيّنُ الشكلُ المجاورُ صفيحةً مِنَ النحاسِ قبلَ صهرِها وتحويلِها إلى مستطيلة المساحةُ نفسُها، أجدُ قياسَينِ ممكنَينِ لطولِ المستطيلِ وعرضِهِ بدلالةِ y

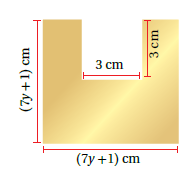
الحل : أولاً نجد مساحة الصفيحة حيث مساحتها عبارة عن نتاج طرح مساحة المربع الصغير من مساحة المربع الكبير :

$A = A_{1} - A_{2}$

$= {(7 y + 1)}^{2} - 3^{3} = {(7 y + 1)}^{2} - 9$

الآن : لنجد قياسين ممكنين لطول المستطيل الجديد وعرضه نحلل المقدار السابق .

${(7 y + 1)}^{2} - 9 = (7 y + 1 - 3) (7 y + 1 + 3)$

$= (7 y - 2) (7 y + 4)$

24) يبيّنُ الشكلُ المجاورُ مخططًا لمستودعَيْ تخزينٍ متجاورَينِ. أكتبُ مقدارًا جبريًّا يمثلُ
الفرقَ بَيْنَ حجمَيِ المستودعَينِ، ثُمَّ أحللُهُ.

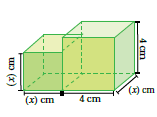
ملاحظة : حجم المستودع $V = l * w * h$

ولإيجاد الفرق بين حجمي المستودعين نطرح حجم المستودع الصغير $V_{2}$ من حجم المستودع الكبير $V_{1}$ كالتالي :

$V = V_{1} - V_{2} = (4 * 4 * x) - (x * x * x)$

$= 16 x - x^{3} = x (16 - x^{2})$

$= x (4 - x) (4 + x)$

25) تحدٍّ: مثلثٌ قائمُ الزاويةِ مساحتُهُ $9 y^{2} - 16$ وحدة مربعة . أجد قياسين ممكنين لطولِ قاعدتِهِ وارتفاعِهِ بدلالةِ y.

ملاحظة : مساحة المثلث تساوي : $A = \frac{1}{2} * b * h$

الحل :

$9 y^{2} - 16 = (3 y - 4) (3 y + 4) = \frac{1}{2} * 2 * (3 y - 4) (3 y + 4)$

$= \frac{1}{2} * (6 y - 8) (3 y + 4)$

إذا $(6 y - 8) (3 y + 4)$ تشكل أبعاد ممكنة .

26) أكتشفُ الخطأَ: حللَ إبراهيمُ المقدارَ $n^{2} - 64$ تحليلً كاملً على النحوِ الآتي:

هَلْ إجابتُهُ صحيحةٌ؟ أبرّرُ إجابتي.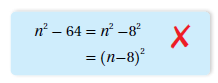

إجابته خاطئة : لأن تحليل : $n^{2} - 8^{2} = (n - 8) (n + 8) \neq {(n - 8)}^{2}$

27) تبريرٌ: أصفُ طريقتَينِ لتبسيطِ ${(2 x - 5)}^{2} - {(x - 4)}^{2}$ وأبيّنُ أيُّ الطريقتَينِ أسهلُ، مبررًا إجابتي.

الطريقة الأولى: احلل المقدار كفرق بين مربعي حدين كالتالي :

${(2 x - 5)}^{2} - {(x - 4)}^{2} = (2 x - 5 - x + 4) (2 x - 5 + x - 4)$

$= (x - 1) (3 x - 9) = 3 (x - 3) (x - 1)$

الطريقة الثانية : نفك القواس ثم اقوم بعملية التبسيط كالتالي :

${(2 x - 5)}^{2} - {(x - 4)}^{2} = 4 x^{2} - 20 x + 25 - (x^{2} - 8 x + 16)$

$= 4 x^{2} - 20 x + 25 - x^{2} + 8 x - 16$

$= 3 x^{2} - 12 x + 9$

$= 3 (x^{2} - 4 x + 3) = 3 (x - 3) (x - 1)$

من الواضح أن طريقة التحليل كفرق بين مربعين أسهل.

28) أكتبُ طريقةَ تحليلِ فرقٍ بَيْنَ مربعَينِ

الحل : نكتب المقدار بصورة ناتج ضرب مجموع حدين في الفرق بينهما .

أسئلة كتاب التمارين :

أحللُ كلًّ مِنَ المقاديرِ الآتيةِ إلى عواملِها:

$1) a^{2} - 49 = (a - 7) (a + 7)$

$2) 100 - w^{2} = (10 - w) (10 + w)$

$3) 9 y^{2} - 36 = 9 (y^{2} - 4) = 9 (y - 2) (y + 2)$

$4) x^{2} y^{2} - 64 = (x y - 8) (x y + 8)$

$5) r^{2} - 0.36 m^{2} = (r - 0.6 m) (r + 0.6 m)$

$6) 24 c^{2} - 6 = 6 (4 c^{2} - 1)$

$= 6 (2 c - 1) (2 c + 1)$

$7) 5 y^{3} m - 45 y m^{3} = 5 y m (y^{2} - 9 m^{2})$

$= 5 y m (y - 3 m) (y + 3 m)$

$8) w^{4} - k^{4} = (w^{2} - k^{2}) (w^{2} + k^{2})$

$= (w - k) (w + k) (w^{2} + k^{2})$

$9) - y^{2} + 144 x^{2} = 144 x^{2} - y^{2}$

$= (12 x - y) (12 x + y)$

$10) \frac{1}{16} y^{2} - \frac{4}{9} = (\frac{1}{4} y - \frac{2}{3}) (\frac{1}{4} y + \frac{2}{3})$

$11) x b^{2} - x^{3} + y^{2} b^{2} - y^{2} x^{2} = (x b^{2} - x^{3}) + (y^{2} b^{2} - y^{2} x^{2})$

$= x (b^{2} - x^{2}) + y^{2} (b^{2} - x^{2})$

$= (b^{2} - x^{2}) (x + y^{2})$

$12) {(3 y + 2)}^{2} - {(2 y + 3)}^{2} = (3 y + 2 + (2 y + 3)) (3 y + 2 - (2 y + 3))$

$= (3 y + 2 + 2 y + 3) ((3 y + 2 - 2 y - 3)$

$= (5 y + 5) (y - 1)$

$= 5 (y + 1) (y - 1)$

أحددُ ما إذا كانَتْ كلُّ ثلاثيةِ حدودٍ ممّا يأتي تمثلُ مربعًا كاملً أَمْ لا، وإذا كانَتْ تمثلُهُ فأحللُها:

$13) x^{2} + 20 x + 100$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي $2 * x * 10$ ؟ نعم

$x^{2} + 20 x + 100 = (x + 10) (x + 10) = {(x + 10)}^{2}$

$14) x^{2} + 10 x + 16$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي $2 * 4 * x$ ؟ لا

إذن ليست مربع كامل

$15) y^{2} - 16 y + 64$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي $2 * y * 8$ ؟ نعم

$y^{2} - 16 y + 64 = (y - 8) (y - 8) = {(y - 8)}^{2}$

$16) w^{2} + 8 w - 16$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ لا ، لأن 16- لا يمكن أن يكون مربع كامل لأنه سالب .

إذن ليست مربع كامل

$17) 4 x^{2} + 12 x + 9$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي $2 * 2 x * 3$ ؟ نعم

$4 x^{2} + 12 x + 9 = (2 x + 3) (2 x + 3) = {(2 x + 3)}^{2}$

$18) 25 x^{2} + 10 x + 1$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي $2 * 5 x * 1$ ؟ نعم

$25 x^{2} + 10 x + 1 = (5 x + 1) (5 x + 1) = {(5 x + 1)}^{2}$

$19) 4 - 4 x + x^{2} = x^{2} - 4 x + 4$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي $2 * x * 2$ ؟ نعم

$x^{2} - 4 x + 4 = (x - 2) (x - 2) = {(x - 2)}^{2}$

$20) \frac{1}{4} w^{2} + 6 w + 36$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي $2 * \frac{1}{2} w * 6$ ؟ نعم

$\frac{1}{4} w^{2} + 6 w + 36 = (\frac{1}{2} w + 6) (\frac{1}{2} w + 6) = {(\frac{1}{2} w + 6)}^{2}$

$21) x^{2} + \frac{2}{3} x + \frac{1}{9}$

1- هل الحد الاول مربع كامل ؟ نعم

2-هل الحد الأخير مربع كامل ؟ نعم

3- هل الحد الأوسط يساوي $2 * x * \frac{1}{3}$ ؟ نعم

$x^{2} + \frac{2}{3} x + \frac{1}{9} = (x + \frac{1}{3}) (x + \frac{1}{3}) = {(x + \frac{1}{3})}^{2}$

تريدُ إيمانُ تغطيةَ جدارٍ مربعِ الشكلِ بورقِ الجدرانِ. إذا كانَتْ مساحةُ الجدار $(x^{2} - 16)$ مترًا مربعًا ، فأجدُ أبعادَ الجدارِ بدلالةِ x

لإيجاد أبعاد الجدار ، نحلل المقدار الجبري المعطى والذي يمثل مساحة الجدار .

$x^{2} - 16 = (x - 4) (x + 4)$

في الشكلِ المجاورِ قرصُ رمايةٍ مساحتُهُ $(x^{2} + 6 x + 9) π c m^{2}$ أجدُ :

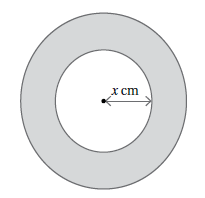
23) نصفَ قطرِ القرصِ بدلالةِ x

24)عرضَ المنطقةِ المظللةِ.

الحل :

$23) A = π r^{2} = π (x^{2} + 6 x + 9)$

$π r^{2} = π (x + 3) (x + 3)$

$π r^{2} = π {(x + 3)}^{2}$

$r^{2} = {(x + 3)}^{2}$

$r = (x + 3) c m$

24) نطرح نصف القطر الصغير x من نصف القطر الكبير 3+x كالتالي :

$24) x + 3 - x = 3 c m$

رياضيات فصل أول

الثامن

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS