تدريب صفحة
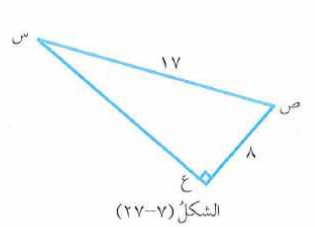
في الشكل : إذا كان فجد كلاً مما يأتي :
جا ع ، جتا ع ،
تدريب صفحة
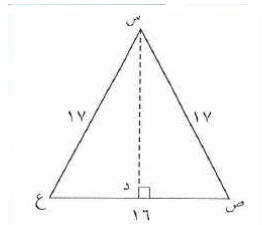
أ ب ج مثلث قائم الزاوية في ب ، فيه أب = ب ج = س فجد :
تدريب صفحة
رصد شخص من النقطة أ مئذنة مسجد ، حيث تبعد النقطة أ عن قمة المئذنة ، فإذا كان قياس الزاوية فجد :
تمارين و مسائل صفحة
أ ب ج مثلث قائم الزاوية في ب ، كما في الشكل جد كلاً مما يأتي :
أ) أب ب) جتا أ ج) جتا ج د) جا أ 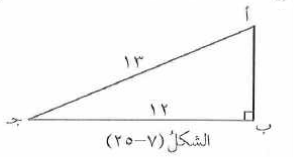
ل م ن مثلث متطابق الضلعين فيه جد : 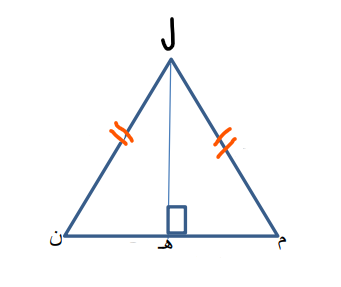
أ) جا م ب ) جتا ن ج) جتا م
يمثل الشكل قطعة أرض على شكل شبه منحرف . احسب محيط قطعة الأرض . 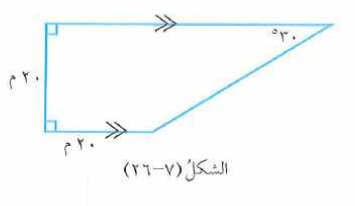
أ ب ج د مستطيل فيه : . 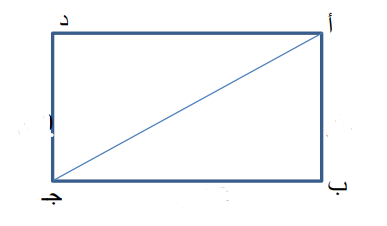
أذا كانت ( س) زاوية حادة ، بحيث جا س = جتا س ، فما قيمة س ؟
جا س = جتا س الضلع المقابل للزاوية س يساوي الضلع الجاور للزاوية س
المثلث متطابق الضلعين
في الشكل جد قياس الزاوية ص .