رياضيات فصل ثاني

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 102

أجدُ المضاعفَ المشتركَ الأصغرَ للمقاديرِ أوِ الحدودِ الجبريةِ المعطاةِ في كلٍّ ممّا يأتي:

$\mathit{a}\mathbf{)} 6b^2 , 12 ab , 18a{b}^4 \mathbf{ }\mathit{b}\mathbf{)} 3b^2-15b-18 , b^3-7b^2+6b$

الحل : 

$\mathit{a}\mathbf{)} 6b^2 , 12ab , 18a{b}^4$ 

بتحليلِ الحدودِ الجبريةِ تحليلًا كاملًا ، ثمَّ كتابةِ العواملِ المُتكرِّرةِ بالصورةِ الأُسِّيَّةِ.	$6b^2$ $12ab$       $18a{b}^4$
بضربِ قوى العواملِ التي لها الأُسُّ الأكبرُ ، والتبسيط	$LCM = 36a{b}^4$

 

---

$\mathit{b}\mathbf{)}\mathbf{ }3b^2 - 15b -18 , b3 - 7b^2 + 6b$

بتحليلِ الحدودِ الجبريةِ تحليلًا كاملًا ، ثمَّ كتابةِ العواملِ المُتكرِّرةِ بالصورةِ الأُسِّيَّةِ.	$3b^2 - 15b -18 = 3(b-6)(b+1)$     $b^3 - 7b^2 + 6b = b(b-6)(b-1)$
بضربِ قوى العواملِ التي لها الأُسُّ الأكبرُ ، والتبسيط	$LCM = 3b(b-6)(b+1)(b-1)$

 

---

أتحقق من فهمي صفحة 104

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورة :

 

$\mathit{a}\mathbf{)} \frac{2x}{x^2 (2x+5)}+\frac{5}{x^2 (5+2x)} \mathit{b}\mathbf{)}\mathbf{ }\frac{5y}{6b^{2}a}+\frac{3b^2}{8a^2} \mathbf{ }\mathbf{ }\mathit{c}\mathbf{)}\mathbf{ }\frac{5}{8x+8}+\frac{x-4}{12x^2+4x-8}$

الحل : 

$\mathit{a}\mathbf{)} \frac{2x}{x^2 (2x+5)}+\frac{5}{x^2 (5+2x)}=\frac{2x+5}{x^2(2x+5)}=\frac{1}{x^2}$                                                        

---

$\mathit{b}\mathbf{)}\mathbf{ }\frac{5y}{6b^{2}a}+\frac{3b^2}{8a^2}=\frac{5y\times 4a}{6b^{2}a\times 4a}+\frac{3b^2\times 3b^2}{8a^2\times 3b^2}=\frac{20ay+9b^4}{24a^2{b}^2}$

---

$\mathit{c}\mathbf{)}\mathbf{ }\frac{5}{8x+8}+\frac{x-4}{12x^2+4x-8}=\frac{5\times (12x-8)}{8(x+1)\times (12x-8)}+\frac{(x-4)\times 8}{(x+1)(12x-8)\times 8}$

$=\frac{60x-40+8x-32}{8(x+1)(12x-8)} =\frac{68x-72}{8(x+1)(12x-8)}=\frac{17x-18}{8(x+1)(3x-2)}$

---

أتحقق من فهمي صفحة 105

صحَّةٌ : صَمَّمَ خالدٌ مُلصَقًا على شكلِ مستطيلٍ للتوعيةِ بأضرارِ التدخينِ في اليومِ العالميِّ للامتناعِ عنِ التدخينِ، وكانَتْ أبعادُهُ كما في الشكلِ المُجاوِرِ. يرغبُ خالدٌ في إحاطةِ المُلصَقِ بإطارٍ. أجدُ طولَ الإطارِ اللازمَ لذلكَ بدلالةِ x في أبسطِ صورةٍ.

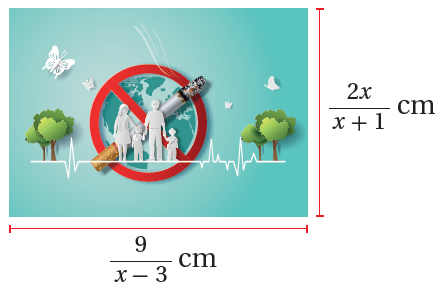الحل :  

$LCM = (x-3)(x+1)$

طول الإطار : $\frac{4x^2+6x+36}{(x+1)(x-3)}cm$

---

أتحقق من فهمي صفحة 106

أُبسِّطُ المقدارَ الآتيَ: $\frac{2+{\displaystyle \frac{1}{y}}}{{\displaystyle \frac{4}{x}}-{\displaystyle \frac{3}{y}}}$

الحل: 

$\frac{2+{\displaystyle \frac{1}{y}}}{{\displaystyle \frac{4}{x}}-{\displaystyle \frac{3}{y}}}=\frac{{\displaystyle \frac{2y}{y}}+{\displaystyle \frac{1}{y}}}{{\displaystyle \frac{4y}{xy}}-{\displaystyle \frac{3x}{xy}}}=\frac{2y+1}{y}÷\frac{4y-3x}{xy}=\frac{2y+1}{y}\times \frac{xy}{4y-3x}=\frac{x(2y+1)}{4y-3x}$
 

---

أسئلة أتدرب وأحل المسائل

أجدُ المضاعفَ المشتركَ الأصغرَ للمقاديرِ أوِ الحدودِ الجبريةِ المعطاةِ في كلٍّ ممّا يأتي:

$\mathbf{1}\mathbf{)} 4m{t}^2, 8m^{3}t, 12m^{4}t$                                                        $\mathbf{2}\mathbf{)} x^2+2x-15 , x^2+6x+5$                 

$\mathbf{3}\mathbf{)}\mathbf{ }{c}^3+5c^2+4c , c{(c+1)}^2$                                                $\mathbf{4}\mathbf{)} 9x^2-16 , 3x^2+x-4$     

الحل : 

$\mathbf{1}\mathbf{)} LCM =24m^4{t}^2$

$\mathbf{2}\mathbf{)} LCM=(x+5\left)\right(x-3\left)\right(x+1)$

$\mathbf{3}\mathbf{)} LCM=c{(c+1)}^2(c+4)$

$\mathbf{4}\mathbf{)}\mathbf{ }LCM=(3x+4\left)\right(3x-4\left)\right(x-1)$

 

 

 

 

 

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ:

$\mathbf{5}\mathbf{)} \frac{6y}{3x^3}+\frac{2}{7y^{2}x}$ 

---

$\mathbf{6}\mathbf{)} \frac{b}{b+3}+\frac{5}{b-2}$   

$=\frac{b(b-2)}{(b+3)(b-2)}+\frac{5(b+3)}{(b+3)(b-2)}=\frac{b^2-2b+5b+15}{(b+3)(b-2)}=\frac{b^2+3b+15}{(b+3)(b-2)}$

---

$\mathbf{7}\mathbf{)}\mathbf{ }\frac{m}{2m-14}+\frac{m^2}{m^2-49}$

$=\frac{m(m+7)}{2(m+7)(m-7)}+\frac{2m^2}{2(m+7)(m-7)}=\frac{m^2+7m+2m^2}{2(m+7)(m-7)}=\frac{3m^2+7m}{2(m+7)(m-7)}$

---

$\mathbf{8}\mathbf{)}\frac{1}{4x^2-12x+9}-\frac{x}{2x^2-x-3}$

$=\frac{x+1}{(2x-3)(2x-3)(x+1)}-\frac{x(2x-3)}{(2x-3)(2x-3)(x+1)}$

$=\frac{x+1-2x^2+3x}{(2x-3)(2x-3)(x+1)}=\frac{4x+1-2x^2}{(2x-3)(2x-3)(x+1)}$

---

 $\mathbf{9}\mathbf{)} \frac{x+3}{x^2 - 1}-\frac{x+2}{x-1}$

$=\frac{x+3}{x^2-1}-\frac{(x+2)(x+1)}{(x-1)(x+1)}=\frac{x+3-x^2-3x-2}{x^2-1}=\frac{-x^2-2x+1}{x^2-1}$

---

 

$\mathbf{10}\mathbf{)} 3s^2-\frac{s+1}{s^2-1}$

$3s^2-\frac{s+1}{s^2-1}=\frac{(s^2-1)\times 3s^2}{s^2-1}-\frac{s+1}{s^2-1}=\frac{3s^4-3s^2-s-1}{s^2-1}$

---

$\mathbf{11}\mathbf{)} \frac{2}{6z-9}-\frac{z-1}{2z^2-3z}$

$=\frac{2z}{3z(2z-3)}-\frac{3(z-1)}{3z(2z-3)}=\frac{2z-3z+3}{3z(2z-3)}=\frac{-(z+3)}{3z(2z-3)}$

---

$\mathbf{12}\mathbf{)}\mathbf{ }\frac{1}{x-y}+\frac{1}{y-x}$

 $=\frac{y-x}{(x-y)(y-x)}+\frac{x-y}{(x-y)(y-x)}=\frac{y-x+x-y}{(x-y)(y-x)}=\frac{0}{(x-y)(y-x)}=0$
 

---

$\mathbf{13}\mathbf{)}\frac{3w-1}{2w^2+w-3}-\frac{2-w}{w-1}$

$=\frac{3w-1}{(2w+3)(w-1)}-\frac{(2w+3)(2-w)}{(2w+3)(w-1)}$

  $=\frac{3w-1-w+2w^2-6}{(2w+3)(w-1)}=\frac{2w-7+2w^2}{(2w+3)(w-1)}$

---

$\mathbf{14}\mathbf{)} \frac{x+2}{x^2+3x-10}+\frac{3}{2-x}$

$=\frac{-(x+2)}{-(x-2)(x+5)}+\frac{3(x+5)}{-(x-2)(x+5)}$

$=\frac{-x-2+3x+15}{-(x-2)(x+5)}=\frac{2x+13}{-(x-2)(x+5)}$

---

$\mathbf{15}\mathbf{)} \frac{2p+3}{p^2-7p+12}-\frac{2}{p-3}$

$=\frac{2p+3}{(p-3)(p-4)}-\frac{2(p-4)}{(p-3)(p-4)}=\frac{2p+3-2p+8}{(p-3)(p-4)}=\frac{11}{(p-3)(p-4)}$

---

$\mathbf{16}\mathbf{)} \frac{3c+1}{c-1}+\frac{c+1}{c^2-4c+3}÷\frac{c-1}{c-3}$

$=\frac{3c+1}{c-1}+\frac{c+1}{(c-3)(c-1)}\times \frac{c-3}{c-1}=\frac{3c+1}{c-1}+\frac{c+1}{(c-1)(c-1)}$

 $=\frac{(c-1)(3c+1)}{(c-1)(c-1)}+\frac{c+1}{(c-1)(c-1)}=\frac{3c^2-c}{(c-1)(c-1)}$

---

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ :

 

$\mathbf{17}\mathbf{)} \frac{6+{\displaystyle \frac{a}{b}}}{2-{\displaystyle \frac{6}{b}}}$

$\frac{6+{\displaystyle \frac{a}{b}}}{2-{\displaystyle \frac{6}{b}}}=\frac{{\displaystyle \frac{6b+a}{b}}}{{\displaystyle \frac{2b-6}{b}}}=\frac{6b+a}{b}\times \frac{b}{2b-6}=\frac{6b+a}{2b-6}$

---

$\mathbf{18}\mathbf{)} \frac{{\displaystyle \frac{6}{x-4}}-{\displaystyle \frac{x}{2x+3}}}{{\displaystyle \frac{2}{2x+3}}+{\displaystyle \frac{2x}{x-4}}}$

$\frac{{\displaystyle \frac{6}{x-4}}-{\displaystyle \frac{x}{2x+3}}}{{\displaystyle \frac{2}{2x+3}}+{\displaystyle \frac{2x}{x-4}}}=\frac{{\displaystyle \frac{x^2+8x+18}{(x-4)(2x+3)}}}{{\displaystyle \frac{4x^2+8x-8}{(x-4)(2x+3)}}}=\frac{-x^2+16x+18}{4x^2+8x-8}$

---

$\mathbf{19}\mathbf{)}\mathbf{ }\frac{{\displaystyle \frac{x}{x-2}}+1}{{\displaystyle \frac{3}{x^2-4}}-1}$

$\frac{{\displaystyle \frac{x}{x-2}}+1}{{\displaystyle \frac{3}{x^2-4}}-1}=\frac{{\displaystyle \frac{2x-2}{x-2}}}{{\displaystyle \frac{7-x^2}{x^2-4}}}=\frac{2x-2}{x-2}\times \frac{(x-2)(x+2)}{7-x^2}=\frac{(2x-2)(x+2)}{7-x^2}$

---

أجدُ محيطَ كلٍّ منَ الشكلينِ الآتيينِ: 

$\frac{2}{3x}+\frac{x+1}{x}+\frac{6}{x^2}=\frac{2x}{3x2}+\frac{3x^2+3x}{3x^2}+\frac{18}{3x^2}=\frac{3x^2+5x+18}{3x^2}cm$

---

$2\times \frac{5}{x-3}+2\times \frac{2x}{x+5}=\frac{10}{x-3}+\frac{4x}{x+5}$

$=\frac{10(x+5)}{(x-3)(x+5)}+\frac{4x(x-3)}{(x-3)(x+5)}=\frac{4x^2-2x+50}{(x-3)(x+5)}m$

---

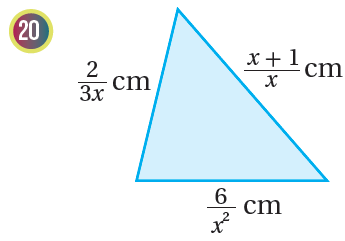
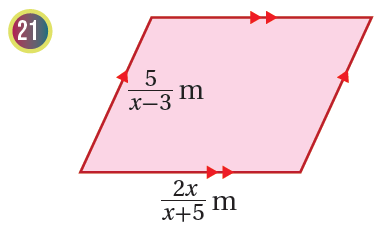
22) رحلةٌ : قرَّرَ مُهنَّدٌ الذهابَ في رحلةٍ بحافلةٍ تسيرُ بسرعةِ $\left(x\right) km/h$، وتقطعُ مسافةَ$60 km$ ، ثمَّ إكمالَ الرحلةِ بسيّارةٍ تسيرُ بسرعةِ $(x+20) km/h$، وتقطعُ مسافةَ $140 km$. أكتبُ الزمنَ الذي سيستغرقُهُ مُهنَّدٌ في الحافلةِ والسيّارةِ في صورةِ مقدارٍ جبريٍّ نسبيٍّ في أبسطِ صورةٍ.

الحل : 

الزمن = المسافة مقسومًا على السرعة 

$\frac{60}{x}+\frac{140}{x+20}=\frac{60(x+20)}{x(x+20)}+\frac{140\left(x\right)}{x(x+20)}=\frac{200 x+1200}{x(x+20)}$

 

 

23) أحل المسألة الواردة في بداية الدرس؟

الحل:

$\frac{4x^3+19x^2+37x+10}{3x(x+1)}$

---

---

مهاراتُ التفكيرِ العليا  

24) أكتشفُ الخطأَ : أكتشفُ الخطأَ في الحَلِّ الآتي، ثمَّ أُصحِّحُهُ.

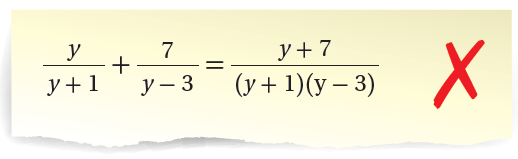
الحل : 

$\frac{y}{y+1}+\frac{7}{y-3}=\frac{y(y-3)}{(y+1)(y-3)}+\frac{7(y+1)}{(y+1)(y-3)}$

$=\frac{y^2-3y+7y+7}{(y+1)(y-3)}=\frac{y^2+4y+7}{(y+1)(y-3)}$

---

25) مسألةٌ مفتوحةٌ : أجدُ مقدارينِ جبريينِ ناتجُ طرحِهِما هوَ: $\frac{x-1}{x+3}$   

الحل : 

$\frac{x}{x+3}-\frac{1}{x+3}=\frac{x-1}{x+3}$

---

26) تبريرٌ: مُثلَّثٌ مُتطابِقُ الأضلاعِ، طولُ ضلعِهِ هوَ: $\frac{7}{6(x-3)}-\frac{1}{x-3}$ تمدَّدَ المُثلَّثُ مُحافِظًا على شكلِهِ، فأصبحَ طولُ ضلعِهِ هوَ: $\frac{x^2}{x-3}-\frac{5}{6(x-3)}$ . أجدُ معاملَ التكبيرِ بدلالةِ x في أبسطِ صورةٍ، مُبرِّرًا إجابتي.

الحل: 

$\frac{{\displaystyle \frac{x^2}{x-3}}-{\displaystyle \frac{5}{6(x-3)}}}{{\displaystyle \frac{7}{6(x-3)}}-{\displaystyle \frac{1}{x-3}}}=\frac{{\displaystyle \frac{6x^2}{6(x-3)}}-{\displaystyle \frac{5}{6(x-3)}}}{{\displaystyle \frac{7}{6(x-3)}}-{\displaystyle \frac{6}{6(x-3)}}}=\frac{6x^2-5}{6(x-3)}÷\frac{1}{6(x-3)}$

$=\frac{6x^2-5}{6(x-3)}\times 6(x-3)=6x^2-5$

 

---

27) تحدٍّ: أُبسِّطُ المقدارَ الآتيَ: $\frac{x}{1-{(1+{\displaystyle \frac{1}{x}})}^{{}^{-1}}}$ 

الحل: 

$\frac{x}{1-{(1+{\displaystyle \frac{1}{x}})}^{-1}}=\frac{x}{1-{\displaystyle \frac{1}{1+{\displaystyle \frac{1}{x}}}}}=\frac{x}{1-{\displaystyle \frac{1}{{\displaystyle \frac{x}{x}}+{\displaystyle \frac{1}{x}}}}}=\frac{x}{1-{\displaystyle \frac{1}{{\displaystyle \frac{x+1}{x}}}}}=\frac{x}{{\displaystyle \frac{x}{x}}-{\displaystyle \frac{x}{x+1}}}=x^2+x$

---

أسئلة كتاب التمارين 

أجدُ المضاعفَ المشتركَ الأصغرَ للمقاديرِ أوِ الحدودِ الجبريةِ المعطاةِ في كلٍّ ممّا يأتي:

$\mathbf{1}\mathbf{)} x^2{y}^{3}z , x{y}^2{z}^4 \mathbf{2}\mathbf{)} x+1 , x^2+x-6$

$\mathbf{3}\mathbf{)}\mathbf{ }{w}^2+w , 3w+3 , w+1 \mathbf{4}\mathbf{)} 6r+2 , 3r , 3r^2+7r+2$

$\mathbf{5}\mathbf{)} y^2+4y+3 , y^2-4y-5 \mathbf{6}\mathbf{)} x^4-8x^3+7x^2 , x^2+2x-3$

الحل:

1) LCM = x2y3z4

2) LCM = (x+3)(x-2)(x+1)

3) LCM = 3w(w+1)

4) LCM = 6r(3r+1)(r+2)

5) LCM =  (y+1)(y+3)(y-5)

6) LCM =  x2(x-7)(x+3)(x-1)

 

 

 

 

  

 

 

 

---

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ : ​​​​​​​

​​​​​​​​​​​​​​

​​​​​​​

 

​​​​​​​

---

 

 

 

 

---

 

​​​​​​​

---

 

---

 

​​​​​​​

 

---

​​​​​​​

 

---

 

​​​​​​​

 

---

 

 

 

مُعتمِدًا المعلوماتِ المعطاةَ في الشكلِ المجاورِ، أُجيبُ عنِ الأسئلةِ الثلاثةِ الآتيةِ تباعًا: 19) أجدُ محيطَ المُربَّعِ في صورةِ مقدارٍ جبريٍّ نسبيٍّ في أبسطِ صورةٍ. 20) أجدُ محيطَ المُثلَّثِ في صورةِ مقدارٍ جبريٍّ نسبيٍّ في أبسطِ صورةٍ. 21) أطرحُ محيطَ المُثلَّثِ منْ محيطِ المُربَّعِ، ثمَّ أكتبُ المقدارَ الجبريَّ النسبيَّ الناتجَ في أبسطِ صورةٍ.

 

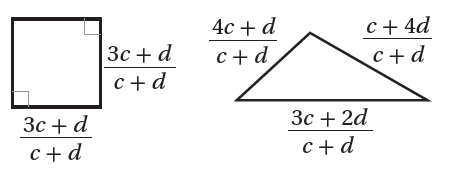الحل : ​​​​​​​​​​​​​​

​​​​​​​​​​​​​​

​​​​​​​

​​​​​​​