أتحقق من فهمي
ص: 65
1) أمثل الاقتران: y=sin x بيانيا في الفترة
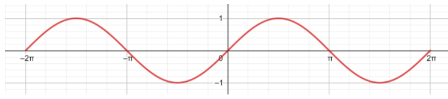
2) أمثل الاقتران: y=cos x بيانيا في الفترة
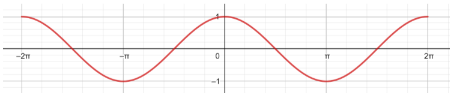
أتحقق من فهمي
ص: 69
أمثل منحنى كل اقتران مما يأتي بيانيا:
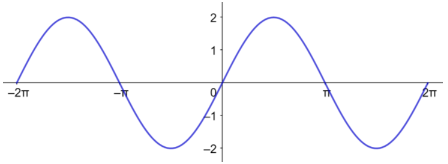

أتحقق من فهمي
ص: 71
أمثل منحنى كل اقتران مما يأتي بيانيا:
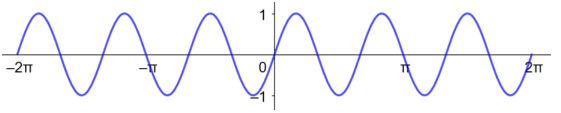

أتحقق من فهمي
ص: 72
أمثل منحنى الاقتران بيانيا.
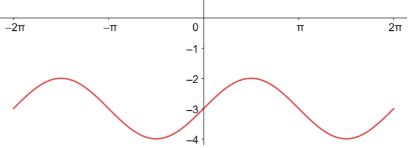
أتحقق من فهمي
ص: 72
أمثل منحنى الاقتران بيانيا.

أتحقق من فهمي
ص: 74
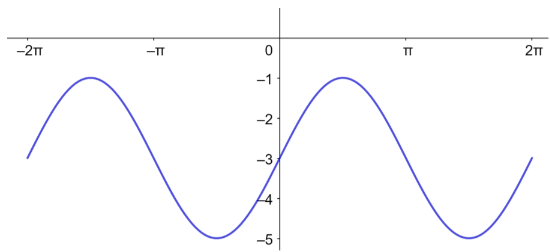
أجد السعة، وطول الدورة، ومعادلة خط الوسط للاقتران: ، ثم أمثلة بيانيا.
السعة=2، طول الدورة= ، معادلة خط الوسط: .
أتحقق من فهمي
ص: 75
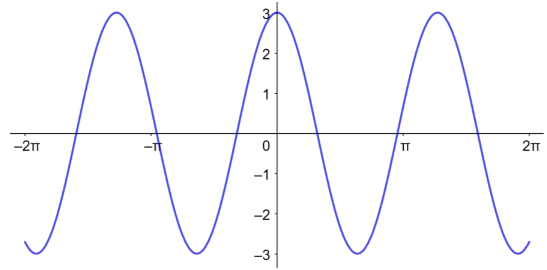
يمثل الاقتران: ازاحة كتلة معلقة في زنبرك بالسنتيمترات، حيث t الزمن بالثواني:
a) أجد أقصى إزاحة، وطول الدورة، والتردد لحركة الكتلة.
أقصى إزاحة=3، طول الدورة=، التردد: .
b) أمثل منحنى إزاحة الكتلة مع الزمن بيانيا.
أتحقق من فهمي
ص: 76
أمثل منحنى الاقتران: بيانيا، ثم أحدد مجاله ومداه.
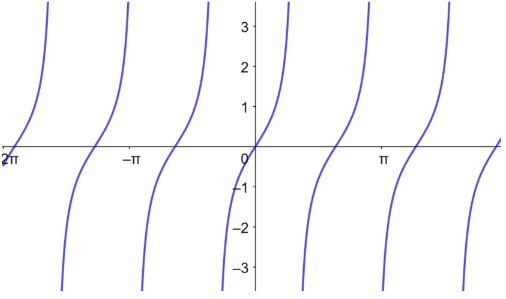
المجال: جميع الأعداد الحقيقية ما عدا n حيث n عدد صحيح فردي
المدى جميع الأعداد الحقيقية.
أتدرب وأحل المسائل
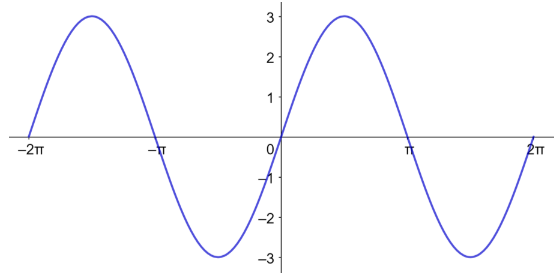
أجد طول الدورة والسعة لكل اقتران مما يأتي، ثم أمثلة بيانيا:
الدورة = ، السعة = 3.
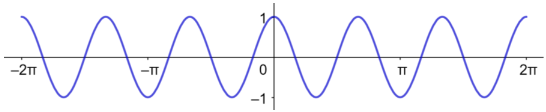
الدورة = ، السعة = 1.
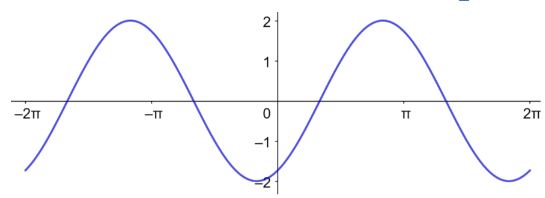
الدورة = ، السعة = 2.
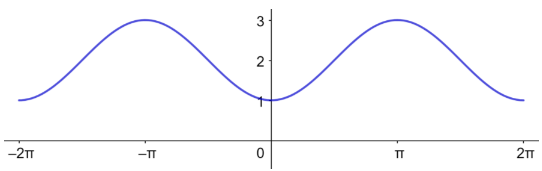
الدورة = ، السعة = 1.
الدورة = 2، السعة = 0.5.
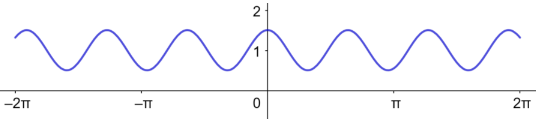
الدورة = ، السعة = 1.
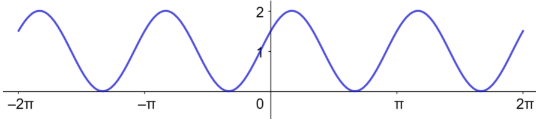
الدورة = ، السعة = 2.
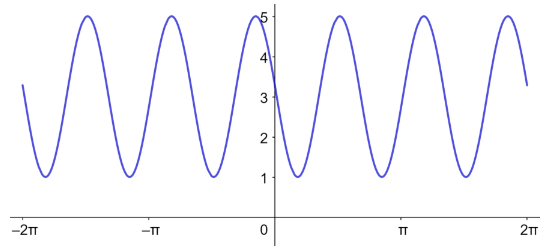
الدورة = ، السعة غير معرفة.
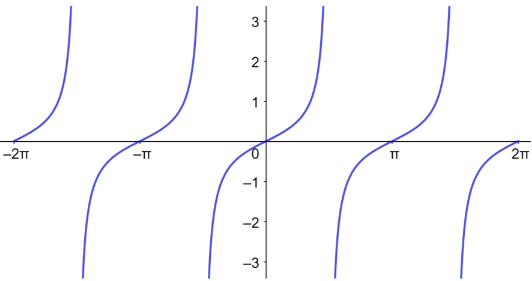
الدورة = ، السعة غير معرفة.
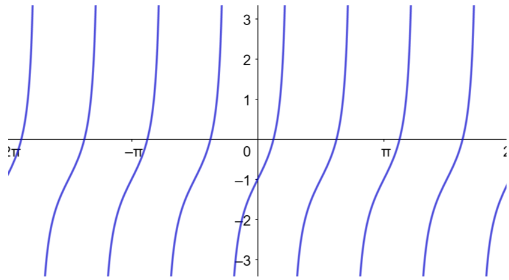
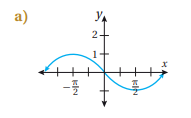
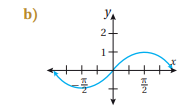
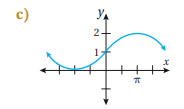
أكتب بجانب كل اقتران مما يأتي رمز التمثيل البياني المناسب له:
f
b
e
a
c
d
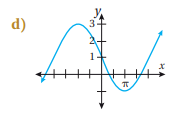
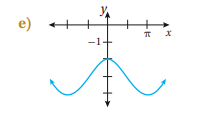
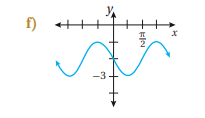
أصف التحويلات الهندسية التي طبقت على منحنى الاقتران f لينتج منحنى الاقتران g في كل مما يأتي:
إزاحة أفقية نحو اليمين مقدارها ، إزاحة رأسية للأعلى مقدارها 1.
توسيع رأسي بمعامل مقداره 3، إزاحة رأسية للأسفل مقدارها 2
إزاحة أفقية نحو اليسار مقدارها ، إزاحة رأسية للأسفل مقدارها 5.
تضييق أفقي بمعامل مقداره ، إزاحة أفقية نحو اليمين مقدارها ، إزاحة رأسية للأعلى مقدارها 9.
عجلة دوارة: تمثل المعادلة: الارتفاع عن سطح الأرض بالأقدام لشخص يركب في عجلة دوارة، حيث t الزمن بالثواني:
20) أمثل منحنى المعادلة ارتفاع الشخص مع الزمن بيانيا.
21) ما أقصى ارتفاع للشخص وأدنى ارتفاع له عن سطح الأرض؟
أقصى ارتفاع:
قدما،
أدنى ارتفاع عندما t=0 بالقدم
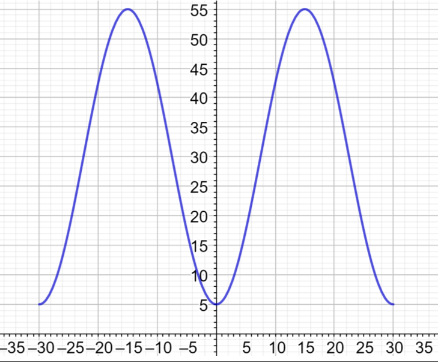
ضغط الدم: يزداد ضغط دم الإنسان في كل مرة ينبض فيها القلب، ثم ينخفض مع راحة القلب بين الضربات. ويمكن نمذجة ضغط دم أحد الأشخاص باستعمال الاقتران: ، حيث: ضغط الدم بوحدة mmHg، وt الزمن بالدقائق:
22) أجد السعة، وطول الدورة، والتردد للاقتران p.
السعة = 25،
طول الدورة = ،
التردد =
23) أمثل منحنى الاقتران p بيانيا.
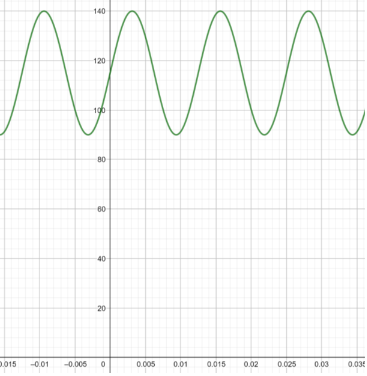
24) إذا كان هذا الشخص يمارس الرياضة، فكيف يؤثر ذلك في طول الدورة والتردد للاقتران p؟
يقل طول الدورة ويزيد التردد، لأنه مع ممارسة الرياضة فإن النبضات تصبح أسرع ويزداد ضغط الدم.
مهارات التفكير العليا
تبرير: أميز الجملة الصحيحة من الجملة غير الصحيحة في ما يأتي، مبررا إجابتي:
25) كل اقتران جيب في الصورة يكتب بوصفه اقتران جيب تمام في صورة .
صحيحة، لأنه يمكن الحصول على منحنى اقتران الجيب بعمل إزاحة أفقية لمنحنى اقتران جيب التمام، والعكس صحيح.
26) طول الاقتران يساوي أربعة أضعاف طول دورة الاقتران .
غير صحيحة، لأن طول دورة الاقتران f (x) يساوي بينما طول دورة الاقتران g (x) يساوي .
27) تحد: استعمل التمثيل البياني المجاور لكتابة قاعدة اقتران في صورة: .
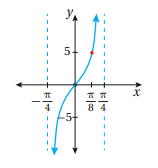
28) تحد: أملأ الفراغ بما هو مناسب في ما يأتي لتصبح المعادلة صحيحة:
أسئلة كتاب التمارين
أجد الدورة والسعة لكل اقتران مما يأتي، ثم أمثلة بيانيا:
السعة = 1، طول الدورة =
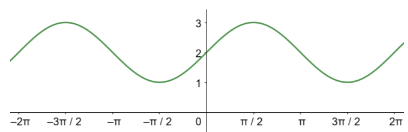
السعة = 1، طول الدورة =
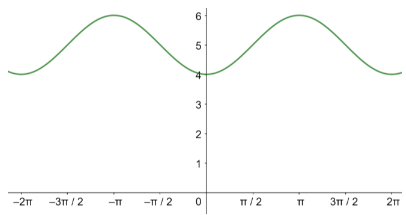
السعة = 1، طول الدورة=

السعة = 1، طول الدورة=
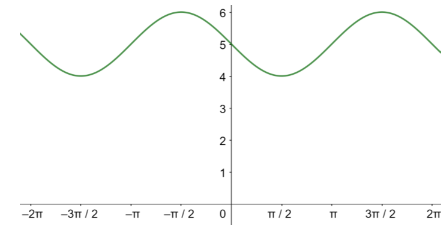
السعة = 1، طول الدورة=
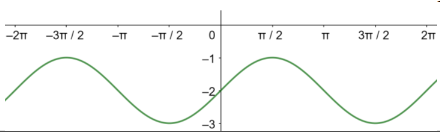
السعة = 1، طول الدورة=
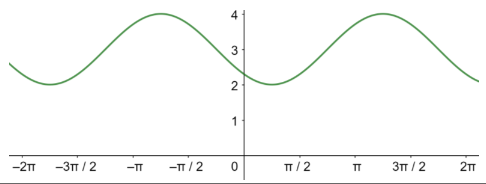
السعة = 4، طول الدورة=
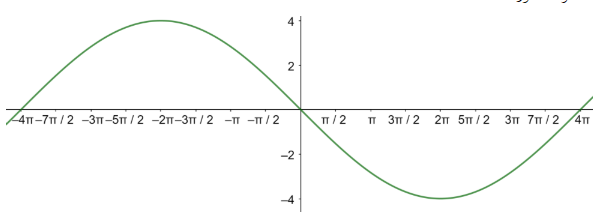
السعة غير معرفة، طول الدورة=
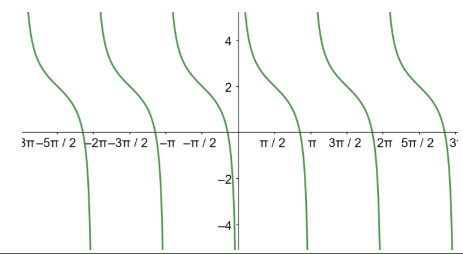
السعة غير معروفة، طول الدورة= 1
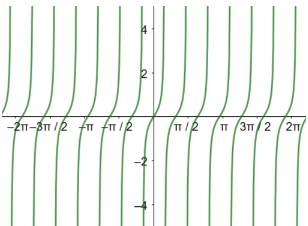
أجد السعة وطول الدورة لكل اقتران مما يأتي، ثم اكتب معادلة في صورة: ، أو صورة: لتمثيل قاعدة الاقتران:
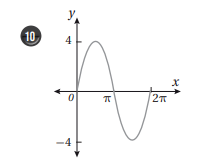
السعة = 4، طول الدورة= ، y=4 sin x
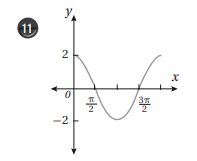
السعة = 2، طول الدورة= ، y=2 cos x
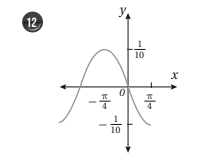
السعة = ، طول الدورة= ، y= sin 2x
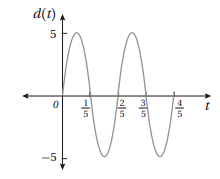
13) يمثل الشكل المجاور الإزاحة d(t) بالسنتمترات مع الزمن t لكتلة معلقة بزنبرك نابضي، وهي تتحرك إلى الأعلى وإلى الأسفل في حركة توافقية بسيطة. أكتب قاعدة الاقتران d، حيث .
أتأمل الشكل المجاور، ثم أجيب عن السؤالين الآتيين:
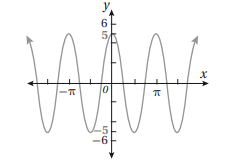
14) هل يمثل المنحنى الاقتران الذي على ، أو أعلى ؟ أبرر إجابتي
رسم لاقتران دوري ولو أخذنا أزواج مرتبة على المنحنى فإنها تحقق الاقتران الجيبي
15) أجد القيمة العظمى، والقيمة الصغرى، وطول الدورة، والسعة للاقتران.
القيمة العظمى = 5 ،
القيمة الصغرى = 5 - ،
طول الدورة = ،
السعة = 5.