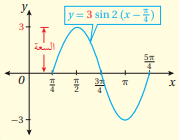
تمثيل الاقترانات المثلثية بيانيًا

 تمثيل الاقترانات المثلثية بيانياً

تمثيل الاقتران: $y=sin\left(x\right)$ ، والاقتران  $y= cos\left(x\right)$ بيانياً

يمكننا تمثيل هذه الاقترانات بيانياً وذلك بإنشاء جدول قيم للمتغيرين x و y وتمثيل كل زوج بنقطة في المستوى مع مراعاة استخدام قياس الزوايا (x) بالراديان في الفترة $\left[0, 2\mathrm{\pi }\right]$

مثال:

أمثل الاقتران $y=\cos x$ في الفترة $\left[0,2\mathrm{\pi }\right]$.

1) أنشئ جدولاً أكتب فيه مجموعة من الزوايا التي نسبها المثلثية معروفة (الزوايا الربعية والزوايا الخاصة).

2) نجد قيمة $cos x$ لكل زاوية x وأكمل الجدول.

x	0	$\frac{\mathrm{\pi }}{3}$	$\frac{\mathrm{\pi }}{2}$	$\frac{2\mathrm{\pi }}{3}$	$\mathrm{\pi }$	$\frac{4\mathrm{\pi }}{3}$	$\frac{3\mathrm{\pi }}{2}$	$\frac{5\mathrm{\pi }}{3}$	$2\mathrm{\pi }$
y= cos x	0	0.5	0	-0.5	-1	-0.5	0	0.5	1
(x,y)	(0,0)	($\frac{\mathrm{\pi }}{3},0.5$)	($\frac{\mathrm{\pi }}{2},0$)	($\frac{2\mathrm{\pi }}{3},-0.5$)	($\mathrm{\pi },1$)	($\frac{4\mathrm{\pi }}{3},-0.5$)	($\frac{3\mathrm{\pi }}{2},0$)	($\frac{5\mathrm{\pi }}{3},0.5$)	($2\mathrm{\pi },1$)

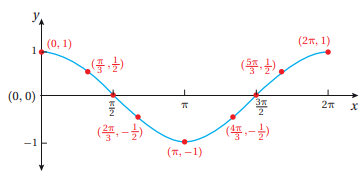
وبنفس الطريقة يمكن رسم الاقتران y=sin x وتالياً الرسم البياني له.

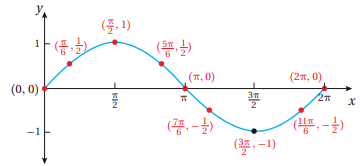
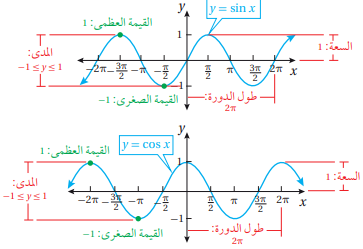
 من خلال التمثيل البياني لكلا الاقترانين $y = \sin \left(x\right) , y= \cos \left(x\right)$ نلاحظ مجموعة من الخصائص لهما:

1) مجال كل منهما هو مجموعة الأعداد الحقيقية

2) مدى كل من الاقترانين هو الفترة $\left[-1, 1\right]$ , وهذا يعني أن القيمة الصغرى لكل منهما هي -1 أما القيمة العظمى لكل منهما هي 1 

3) سعة منحنى الاقتران هي نصف الفرق بين القيمة العظمى والقيمة الصغرى وتساوي 1 لكلا الاقترانين لأن:

$\frac{1}{2}(1-(-1\left)\right) = 1$

4) كل من الاقترانين هو اقتران دوري، أي أن التمثيل البياني لمنحنى كل منهما له نمط متكرر وأن أقصر جزء متكرر يعبر عن الدورة

5) الطول الأفقي لكل دورة يسمى طول الدورة حيث أن التمثيل البياني يظهر أن طول الدورة لكل منهما هو  $2\mathrm{\pi }$

الاقترانات الجيبية

والآن سنتعرف على الاقترانات الجيبية مفهومها والتمدد الرأسي والأفقي والانسحاب الرأسي والأفقي لها وانعكاسها 

الاقترانات الجيبية:

هي اقترانات الجيب وجيب التمام الناتجة من تحويل هندسي أو أكثر لمنحنى الاقترانين الرئيسين: $y = \sin \left(x\right) , y= \cos \left(x\right)$ وصورتهما العامة هي: 

$$\begin{gathered} y = a\cos \left(bx-c\right)+d \\ y = a\sin \left(bx- c\right) +d \end{gathered}$$

حيث a, b, c, d أعداد حقيقية وa و b لا يساويان صفر

التمدد الرأسي للاقترانات الجيبية:

ينقسم إلى قسمين:

1) توسيع رأسي: ويحدث ذلك إذا كان $\left|a\right|>1$ ، فإن المعامل a في الاقترانين: $y =a\cos \left(x\right) , y = a\sin \left(x\right)$ يؤدي إلى توسيع رأسي للمنحنيين.

2) تضييق رأسي: ويحدث ذلك إذا كان $\left|a\right|<1$ ، فإن المعامل a في الاقترانين يؤدي إلى تضييق رأسي للمنحنيين

أي أن قيمة a تؤثر في سعة الاقترانات الجيبية

سعة الاقترانات الجيبية:

سعة منحنى الاقتران الجيبي هي نصف المسافة بين قيمتيه العظمى والصغرى، أو نصف ارتفاع الموجة. سعة كل من: $y=a \sin (bx-c)+d$،                     و $y=a \cos (bx-c)+d$                   ،هي $\left|a\right|$.

ملاحظة:

تحديد قيمة السعة تساعد على تمثيل الاقترانات الجيبية بيانياً حيث أننا نحتاج إلى تحديد نقاط تقاطع الاقترانات الجيبية مع المحور x ثم نستعمل قيمة السعة لتحديد نقاط عظمى وصغرى للاقتران الجيبي ومن ثم نرسم الموجة التي تمر بهذه النقاط.

مثال:

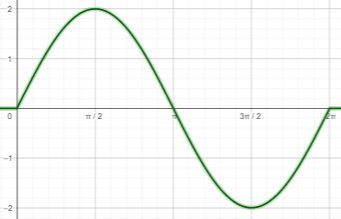
أمثل منحنى كل من الاقترانات الآتية بيانياً:

$1) g(x)= 2\sin \left(x\right)$

1) أحدد سعة الاقتران g (x) وهي $\left|2\right|=2$ .

2) أحدد إحداثيات نقاط تقاطع منحنى الاقتران f (x) =sin x مع المحور x والنقاط العظمى والصغرى له.

أحدد إحداثيات نقاط تقاطع منحنى الاقتران f (x) =sin x مع المحور x

$sin x=0, x=\left\{0,\mathrm{\pi },2\mathrm{\pi }\right\}$

القيمة العظمى للاقتران f(x)=sin x تساوي 1 

القيمة الصغرى للاقتران f(x)=sin x تساوي 1- 

3) أضرب الإحداثي y لكل نقطة عظمى أو صغرى على منحنى الاقتران f (x) في سعة الاقتران g (x)، لإيجاد النقاط المقابلة لها على منحنى الاقتران g.

القيمة العظمى للاقتران g(x)=2 sin x تساوي 2×1=2.

القيمة العظمى للاقتران g(x)=2 sin x تساوي 2×1-=2-.

4) أمثل منحنى الاقتران g (x) اعتماداً على النقاط الجديدة.

$2) g(x) = \frac{1}{5}\cos \left(x\right)$

بنفس خطوات المثال السابق نمثل منحنى هذا الاقتران.

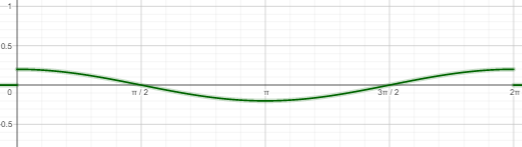
التمدد الأفقي للاقترانات الجيبية:

ينقسم إلى قسمين:

1) توسيع أفقي: إذا كان $\left|b\right|<1$ فإن المعامل b في الاقترانين  $y = \cos \left(bx\right) , y=\sin \left(bx\right)$ يؤدي إلى توسيع أفقي لمنحنى كل من الاقترانين

2) تضييق أفقي: إذا كان $\left|b\right|>1$ فإن المعامل لا يؤدي إلى تضييق أفقي لكلا المنحنيين.

طول دورة الاقترانات الجيبية:

طول دورة الاقتران الجيبي هو المسافة بين مجموعتين متكررتين من النقاط على منحناه. طول الدورة كل من: $y=a \sin (bx-c)+d$،و $y=a \cos (bx-c)+d$، هو $\frac{2\mathrm{\pi }}{\left|b\right|}$، حيث: $b\ne 0$.

ملاحظة: 

تحديد طول الدورة الجيبية يساعد في تمثيل الاقترانات الجيبية وذلك من خلال إيجاد النقاط المفتاحية للاقترانات الجيبية الرئيسة ثم نضرب الإحداثي x لكل نقطة مفتاحية في $\frac{1}{b}$

مثال:

أمثل منحنى كل اقتران مما يلي بيانياً

$1) g(x)= \sin \left(2x\right)$

1) أحدد طول دورة الاقتران g (x) وهي:

$\frac{2\mathrm{\pi }}{\left|b\right|}=\frac{2\mathrm{\pi }}{\left|2\right|}=\mathrm{\pi }$

2) أحدد إحداثيات نقاط تقاطع الاقتران f (x) = sin x مع المحور x والنقاط العظمى والصغرى له في الفترة $\left[0,2\mathrm{\pi }\right]$.

3) أضرب الإحداثي x لكل نقطة مفتاحية على منحنى الاقتران f (x) في 0.5، لإيجاد النقاط المقابلة لها على منحنى الاقتران g (x).

4) أمثل منحنى الاقتران g (x) اعتماداً على النقاط الجديدة.

$2) g(x)=\cos \left(\frac{x}{2}\right)$

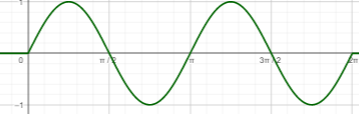
وبنفس خطوات المثال السابق نمثل منحنى هذا الاقتران.

الانسحاب الرأسي للاقترانات الجيبية:

يتذبذب منحنيا الاقترانين الرئيسين : $y = \cos \left(x\right) , y= \sin \left(x\right)$ حول المحور x ولكن عند إجراء انسحاب رأسي للاقتران الجيبي فإن منحناه يتذبذب حول محور جديد يسمى خط الوسط

وبصورة عامة يكون خط الوسط للاقتران الجيبي  $y = a\sin \left(bx-c\right)+d$ أو منحنى الاقتران الجيبي  $y = a\cos \left(bx-c\right)+d$ هو y=d.

مثال: 

أمثل منحنى الاقتران g (x) = -1 +sin x بيانياً

منحنى الاقتران g (x) هو نفس منحنى الاقتران f (x) =sin x مزاحاً للأسفل بمقدار وحدة واحدة.

الانسحاب الأفقي للاقترانات الجيبية:

1) منحنى الاقتران $g\left(x\right) = f(x+c), c>0$ هو منحنى الاقتران f (x) مزاحاً c وحدة إلى اليسار

2) منحنى الاقتران $g\left(x\right) = f(x-c)$ هو منحنى الاقتران f (x) مزاحاً c وحدة إلى اليمين

مثال:

أمثل منحنى الاقتران  $g\left(x\right) = \sin \left(x+\frac{\mathrm{\pi }}{3}\right)$ بيانياً

منحنى الاقتران g (x) هو نفس منحنى الاقتران f (x) =sin x مزاحاً لليسار بمقدار $\frac{\mathrm{\pi }}{3}$.

انعكاس الاقترانات الجيبية:

إذا كانت $a<0$ فإن

1) منحنى الاقتران $y= a\sin \left(bx-c\right)+d$ يكون انعكاساً لمنحنى الاقتران $y = \left|a\right|\sin \left(bx-c\right)+d$ 

2) منحنى الاقتران $y = a\cos \left(bx-c\right)+d$ يكون انعكاساً لمنحنى الاقتران $y = \left|a\right|\cos \left(bx-c\right)+d$

مثال:

أجد السعة وطول الدورة ومعادلة خط الوسط للاقتران $f\left(x\right) = - \frac{1}{2}\sin \left(x-\frac{\mathrm{\pi }}{2}\right)-1$ ثم أمثله بيانياً.

السعة = $\left|-\frac{1}{2}\right|=\frac{1}{2}$, طول الدورة = $\frac{2\mathrm{\pi }}{\left|b\right|}=\frac{2\mathrm{\pi }}{\left|1\right|}=2\mathrm{\pi }$. معادلة خط الوسط y=-1.

الحركة التوافقية:

مثال:

أجد أقصى إزاحة ودورة الاقتران والتردد لحركة كتلة معلقة في زنبرك حيث أن إزاحتها بالسنتيمترات تعطى بالعلاقة $y =5 \cos \left(2\mathrm{\pi t}\right)$ .

أقصى إزاحة :

 $\left|5\right|=5$،

طول الدورة:

 $\frac{2\mathrm{\pi }}{\left|b\right|}=\frac{2\mathrm{\pi }}{2\mathrm{\pi }}=1$،

التردد :

 $\frac{\omega }{2\mathrm{\pi }}=\frac{2\mathrm{\pi }}{2\mathrm{\pi }}=1$.

 تمثيل اقتران الظل:

نستخدم نفس الطريقة المستخدمة في الاقترانات الجيبية لتمثيل اقتران الظل مع مراعاة أن منحنى اقتران الظل له خطوط تقارب رأسية عندما $\cos \left(x\right)=0$ لأن $\tan \left(x\right)= \frac{\sin \left(x\right)}{\cos \left(x\right)}$

خصائص اقتران الظل:

مثال:

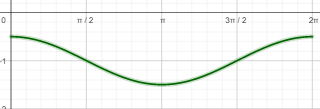
أمثل منحنى الاقتران: $g\left(x\right) = \tan \left(x\right)+1$ ، ثم أحدد مجاله ومنحناه.

منحنى الاقتران g (x) هو نفس منحنى الاقتران f (x) =tan x مزاحاً إلى الأعلى وحدة واحدة.

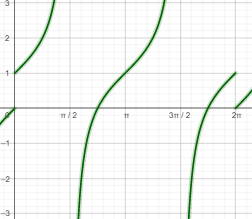
مجال الاقتران هو جميع الاعداد الحقيقية، ما عدا $\frac{\mathrm{\pi }}{2}n$، حيث n عدد صحيح فردي، ومداه حميع الأعداد الحقيقية.