تصنيف الأشكال الرباعية
فكرة الدرس : أصنف الأشكال الرباعية حسب أضلاعها وزواياها.
•• الشكل الرباعي (Quadrilateral) : مضلع له 4 أضلاع و 4 زوايا، وتُصنف الأشكال الرباعية وفقًا لخصائص أضلاعها وزواياها.
| شبه المنحرف (Trapizoid) : شكل رباعي فيه ضلعان متقابلان متوازيان. | 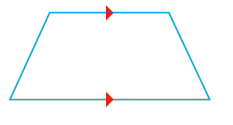 |
| متوازي الأضلاع (Parallelogram) : شكل رباعي فيه كل ضلعين متقابلين متوازيين ومتطابقين. | 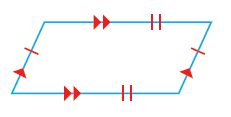 |
| المستطيل (Rectangle) : هو متوازي أضلاع زواياه قوائم. | 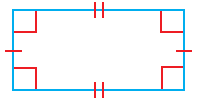 |
| المعين (Rhombus) : هو متوازي أضلاع أضلاعه متطابقة. | 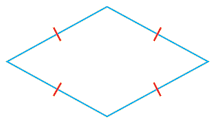 |
| المربع (Square) : هو متوازي أضلاع أضلاعه متطابقة وزواياه قوائم. | 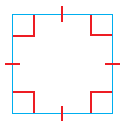 |
مثال:
أصنف كل مما يأتي إلى أكبر عدد ممكن من الأشكال الرباعية:

الحل :
|
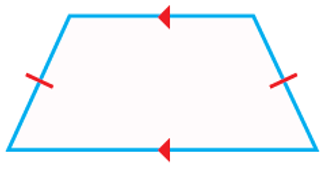
ألاحظ من الشكل الرباعي المجاور أن: • فيه فقط ضلعان متوازيان متقابلان، إذن الشكل شبه منحرف. |
 |
|
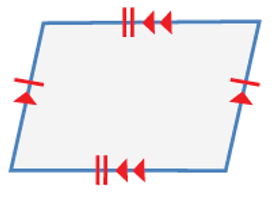
ألاحظ من الشكل الرباعي المجاور أن: • زواياه ليست قوائم. • فيه كل ضلعين متقابلين متوازيين ومتطابقين. إذن الشكل الرباعي متوازي أضلاع. |
 |
|
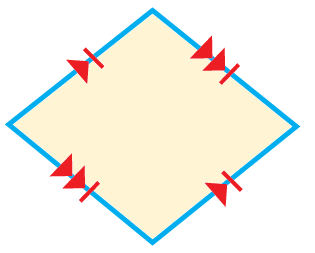
ألاحظ من الشكل الرباعي المجاور أن: • زواياه ليست قوائم. • فيه كل ضلعين متقابلين متوازيين. • أضلاعه متطابقة . إذن الشكل الرباعي متوازي أضلاع ومعين. |
 |
يُمكن استنتاج بعض العلاقات بين الأشكال الرباعية ، ويمكن تلخيصها في المخطط الآتي :
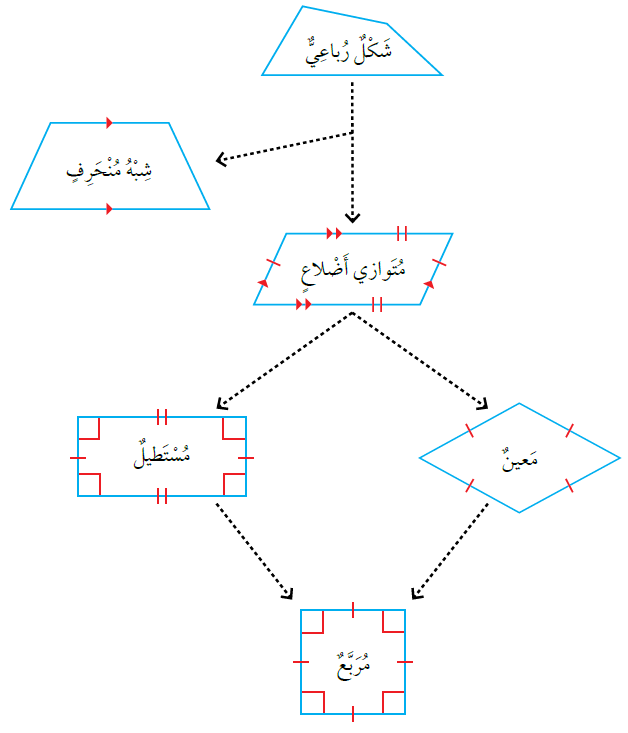
مثال :
أبين صحة كل عبارة مما ياتي أو عدم صحتها ، مُبررًا إجابتي :
1) كل مستطيل مربع .
عبارة غير صحيحة : لأن المستطيل فيه كل ضلعين متقابلين متطابقين ومتوازيين ولا يشترط تطابق الأضلاع الأربعة كما في المربع .
2) كل مربع مستطيل .
عبارة صحيحة : لأن كل مربع فيه كل ضلعين متقابلين متوازيين ومتطابقين ، وهذا يتحقق في المستطيل .
3) كل مستطيل متوازي أضلاع .
عبارة صحيحة : لأن كل مستطيل فيه كل ضلعين متقابلين متوازيين ومتطابقين ، وهذا يتحقق في متوازي الأضلاع .
4) كل متوازي أضلاع مستطيل .
عبارة غير صحيحة : لأن زوايا متوازي الأضلاع قد تكون غير قائمة ، بينما يشترط الزوايا القائمة في المستطيل.