رياضيات فصل ثاني

تعلمنا سابقا كيفية إجراء العمليات الحسابية الأربعة ( الجمع والطرح والضرب والقسمة) على كثيرات الحدود لتكوين اقترانات جديدة.

---

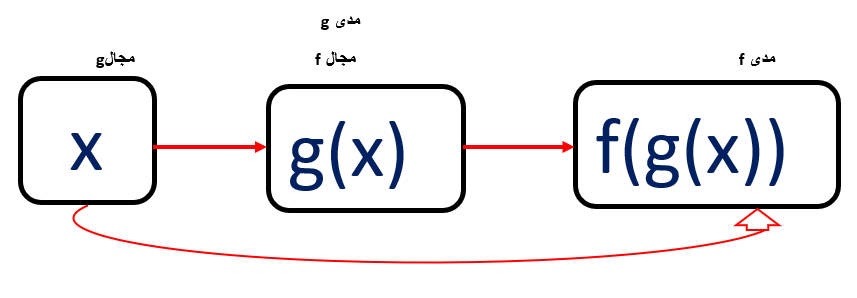
أيضا يمكن تكوين اقتران جديد من الاقترانين f(X) و g(x) و ذلك عن طريق دمجهما بحيث تكون مخرجة أحدهما هي مدخلة للآخر 

فتسمى عملية الدمج     تركيب الاقترانات ويسمى الاقتران الناتج عن ذلك بالاقتران المركب 

• يمكن تركيب الاقترانين g(x) و f(x) بطريقتين هما 

1)  تطبيق g اولا ثم تطبيق f على نتيجة g ويرمز له $( f\circ g)$

2) تطبيق f اولا ثم تطبيق g على نتيجة f ويرمز له $( g\circ f)$

مفهوم أساسي :

تركيب الاقترانات 

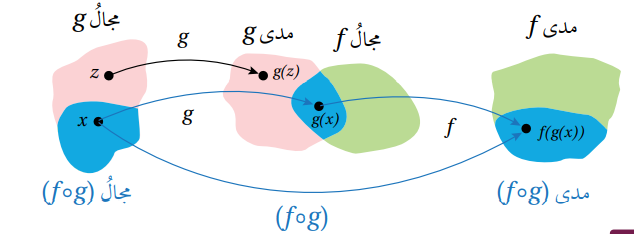
إذا كان f(X) و g(x) اقترانين وكان مدى g(x) يقع ضمن مجال f(x) فإن الاقتران المركب $(f\circ g)\left(x\right)$ يعطى كما يأتي   $( f\circ g)\left(x\right) =f\left(g\right(x\left)\right)$

مثال 

إذا كان f(x)= x² +2  وكان  g(x) = 3 - x ، جد ما يلي :

1. $( g\circ f)\left(1\right)=g\left(f\right(1\left)\right)=g(1+2)=g\left(3\right)=3-3=0$ 

 

 2.  $( f\circ g)(-3)=f\left(g\right(-3\left)\right)=f(3-(-3\left)\right)=f\left(6\right)=36+2=38$ 

---

 

• يمكن إيجاد  قاعدة الاقتران المركب بدلالة المتغير x

مثال:

إذا كان f(x) = 2x - 3 وكان g(x) = x² فأجد قاعدة كل من : 

1. $(f\circ g)\left(x\right)= f\left(g\right(x\left)\right)= f( x^2 )=2( x^2)-3=2 x^2-3$

 

 2. $( g\circ f)\left(x\right)=g( f(x\left)\right)=g(2x-3)= {(2x-3)}^2=4x^2-12x+9$

     

---

مجال الاقتران المركب

 

يتكون مجال $( f\circ g)\left(x\right)$ من مجموعة قيم x من مجال g التي تكون قيم  g(x)  لها موجودة في مجال f. ولذلك تستثنى من مجال $( f\circ g)\left(x\right)$ قيم x  التي لا يكون الاقتران  g معرفا عندها ( ليست ضمن مجال g) ، وقيم x التي لا يكون  $f\left(g\right(x\left)\right)$  معرفا عندها g(x) ليست ضمن مجال f.

مثال 

إذا كان $f\left(x\right)=\frac{-3}{x+2}$  و كان $g\left(x\right)=\frac{4}{2x-8}$  ، جد مجال الاقتران $( f\circ g)\left(x\right)$

مجال الاقتران (x)g هو مجموعة الأعداد الحقيقية باستثناء قيم x  التي تجعل المقام صفرا .

$2x-8=0\to x=4$

مجال الاقتران (x)f هو مجموعة الأعداد الحقيقية باستثناء قيم x  التي تجعل المقام صفرا .

$x+2=0\to x=-2$

 

ولذلك نستثني قيم x التي تجعل g(x) = -2 

g(x) = -2

$\frac{4}{2x-8}=-2\to 4=-2(2x-8)$

$\to 4=-4x+16\to -20=4x\to x=-5$

إذا مجال $(f\circ g)\left(x\right)$ هو مجموعة الأعداد الحقيقية باستثناء  x = 4 , x = -5 أي $\{x:x\ne 4,x\ne -5 \}$

---

 

•  يمكن النظر إلى كثير من الاقترانات بوصفها اقترانات مركبة و إيجاد اقترانين بسيطين يكافئ يركيبهما الاقتران المركب عند إذ يكون الاقترانان البسيطان مركبتي الاقتران المركب 

مثال:

أجد الاقترانين f(x) و g(x)  بحيث يمكن التعبير عن كل من الاقترانين الآتيين بالصورة  h(x) = f( g(x)) 

 $1) h(x)=\frac{1}{x+3}$

أفترض أن    $f\left(x\right) =\frac{1}{x}$ ,  g(x) = x +3 . وبذلك فإن :

 

بتعويض f( g(x)) = f( x+3)                                         g(x) = x +3

بتعويض  x +3  مكان x  في معادلة  f                                     $=\frac{1}{x +3 }= h\left(x\right)$                  

            

$2) h(x)={(2+x^2)}^{10}$ 

أفترض أن f(x) = x¹⁰ و g(x) = 2 + x²  وبذلك ، فإن :

                                                                                

 

---

•  
• يمكن استعمال فكرة الاقترانات المركبة في مواقف حياتية كثيرة مثل : التجارة ، والصناعة ، وغيرهما.

مثال

صناعة : وجد مدير مصنع للأثاث أن تكلفة إنتاج q من خزانات الكتب في فترة العمل الصباحية بالدينار هي : $C\left(q\right) = q2 +2q +800$ . إذا كان عدد خزانات الكتب التي يمكن إنتاجها في t ساعة في الفترة الصباحية هي :   $0\le t\le 5$  ,q(t) = 20t فما تكلفة الإنتاج بدلالة t ؟ كم دينارا تكلفة الإنتاج في نهاية ساعة العمل الرابعة ؟

لإيجاد تكلفة الإنتاج بدلالة t ، أعوض قيمة q(t)  في معادلة التكلفة ، فأكون اقترانا مركبا هو $( c\circ q)\left(t\right)$:

$( c\circ q)\left(t\right) =c\left(20t\right)={\left(20t\right)}^2+2\left(20t\right)+800=400t^2+40t+800$

تكلفة الإنتاج في نهاية ساعة العمل الرابعة هي : $( c\circ q)\left(4\right)$

$(c\circ q)\left(4\right)=400\left(16\right)+40\left(4\right)+800=7360$   

إذا تكلفة الإنتاج في نهاية ساعة العمل الرابعة هي : 7360 دينارا   

---