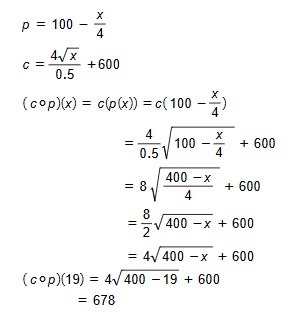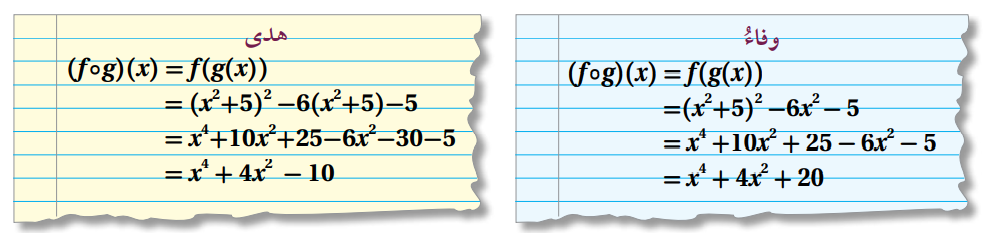أتحقق من فهمي صفحة 26
إذا كان h(x) = , j(x) = 2x +1 , فأجد كلا مما يأتي :
a. = h(j(4)) = h(2(4)+1= h(9) = = 3
b. = j(h(4)) = j() = j(2) = 2(2) +1 = 5
c. = h(h(16)) = h( ) = h(4) = = 2
d. = j(j(-8)) = j( 2(-8) +1) = j(-15) = 2(-15) +1 = -29
أتحقق من فهمي صفحة 27
إذا كان f(x) = x2 +4x , g(x) = 2 -3x ، فأجد قاعدة كل من : و ثم أجد , و
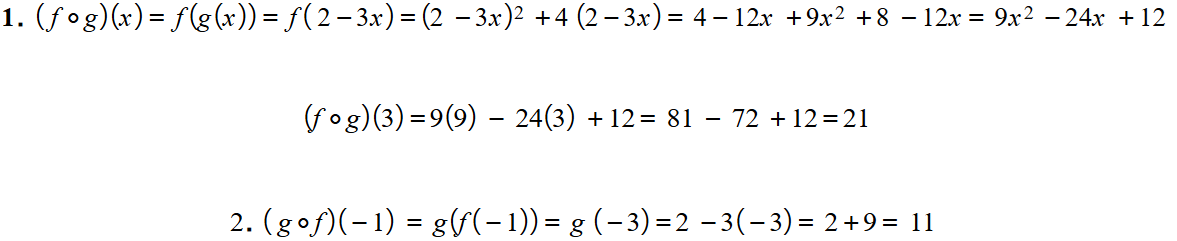
أتحقق من فهمي صفحة 28
أجد مجال للاقترانين في المثال أعلاه.( مثال 3)
مثال 3
, إذا كان
الحل :
مجال (x)f هو مجموعة الأعداد الحقيقية ما عدا x = 2
مجال g(x) هو مجموعة الأعداد الحقيقية ما عدا x = 3
مجال هو مجموعة الأعداد الحقيقية ما عدا
أتحقق من فهمي صفحة 29
أجد الاقترانين f(x) و g(x) بحيث يمكن التعبير عن كل من الاقترانين الآتيين بالصورة h(x) = f(g(x))
a. h(x) = 4x2 -1
g(x) = x2
f(x) = 4x- 1
.b
g(x) = x+2
أتحقق من فهمي صفحة 30
قياس : يحول الاقتران درجات الحرارة من المقياس الفهرنهايتي F إلى مقياس سيلسيوس C. ويحول الاقتران k(c) = c +273 درجات الحرارة من مقياس سيلسيوس إلى مقياس كلفن K . أكتب الاقتران الذي يحول درجة الحرارة من المقياس الفهرنهايتي إلى مقياس كلفن ، ثم أجد درجة الحرارة على مقياس كلفن التي تقابل 86 درجة فهرنهايتية.
أتدرب و أحل المسائل
إذا كان ,f(x) = x + 7 , فأجد كلا مما يأتي :
إذا كان c(x) = x3 , d(x) = 2x - 3 فأجد كلا مما يأتي :
أجد مجال في كل مما يأتي :
مجال g(x) هو مجموعة الأعداد الحقيقية ماعدا x= 5
مجال f(x) هو مجموعة الأعداد الحقيقية ما عدا x=3
مجال هو مجموعة الأعداد الحقيقية ما عدا
مجال g(x) هو مجموعة الأعداد الحقيقية ماعدا x= -7
مجال f(x) هو مجموعة الأعداد الحقيقية ما عدا x=1
مجال هو مجموعة الأعداد الحقيقية ما عدا
11. إذا كان a(x) = x + 4 , b(x) = x - 7 فأثبت أن
الحل
12. إذا كان f(x) = 2x , g(x) = 3x +4 فأجد ثم أجد قيمة
f(g(x)) = f( 3x+4) = 2(3x+4)
13. إذا كان g(x) 2x -10 , فأجد بصورة كسر واحد ، ثم أعين مجاله.
المجال : مجموعة الأعداد الحقيقية ما عدا x = 4
إذا كان f(x) = x + 1 , g(x) = x2 -7 فأعبر عن كل مما يأتي بصورة اقتران مركب ، معتمدا الاقترانين f , g :
أجد اقترانين f(x) و g(x) بحيث يمكن التعبير عن كل من الاقترانين الآتيين بالصورة h(x) = f(g(x))
الحل
الحل
18. إذا كان فهل يمكن تكوين ؟ أبرر إجابتي
الحل :
مدى g(x) هو جميع الأعداد الحقيقية السالبة ، وهي غير موجودة في مجال f(x) لأن مجال f(x) هو الأعداد الحقيقية التي لا تقل عن 2، فلا يمكن تكوين
19. أحل المسألة الواردة في بداية الدرس.
عندما تسقط قطرة ماء المطر على بحيرة تتكون موجة دائرية يتزايد طول نصف قطرها بالنسبة إلى الزمن وفق الاقتران:
حيث r نصف القطر بالسنتيمترات ، و t الزمن بالدقائق. أجد مساحة الموجة عندما t= 2 .
الحل
يعطى عدد خلايا البكتيريا في أحد الأطعمة المبردة في الثلاجة بالاقتران: حيث T درجة حرارة الطعام . عند إخراج الطعام من الثلاجة تعطى درجة حرارته بالاقتران T(t) = 5t +1.5 حيث t الزمن بالساعات :
20. أكتب الاقتران :
N(T(t)) = N( 5t +1.5)
= 23(5t +1.5)2 - 56(5t +1.5) +1
= 23( 25t2 +15 t +2.25) -280t -84 +1
= 575 t2 +345 t +51.75 -280t - 83
= 575 t2 +65 t -31.25
21. أجد الزمن الذي يصل عنده عدد خلايا البكتيريا إلى 6752 مقربا إجابتي إلى منزلتين عشريتين.
الحل
مرفوضة
22. إذا كان , f(x) = ax+b و كان فأجد قيمة كل من a و b
f(f(x)) = f(ax +b)
= a(ax +b) +b
= a2x +ab +b
a2x +ab +b = 16x -15
a2 = 16 and ab +b = -15
a = 4 , a = -4 مرفوضة
ab +b = -15
4b +b = -15
5b = -15
b = -3
23. أجد في أبسط ، علما بأن : f(x) = x2 +1 , g(x) = , h(x) = x+3
الحل
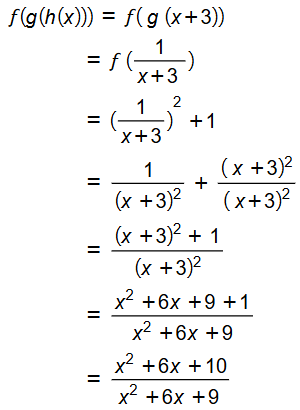
مهارات التفكير العليا
24. أكتشف الخطأ: وجدت كل من هدى ووفاء ناتج ، حيث f(x) = x2 -6x -5 , g(x) = x2 +5 أحدد إذا كانت إجابة أي منهما صحيحة ، مبررا إجابتي .
f( g(x)) = f( x2 +5)
= (x2 +5)2 - 6(x2 +5) - 5
= x4 +10x2 +25 -6x2 -30 -5
= x4 +4x2 - 10
إذا إجابة هدى صحيحة وإجابة وفاء خاطئة
25. مسألة مفتوحة : أكتب اقترانين f و g بحيث يكون
g(x) = x2 - 4x
f(x) = x+ 7
26. تحد : إذا كان فما قاعدة ؟ ما مجاله ؟
مجال g(x) هو مجموعة الأعداد الحقيقية ما عدا x = -2
مجال f(x) هو مجموعة الأعداد الحقيقية ما عدا x = 3
مجال هو مجموعة الأعداد الحقيقية ما عدا
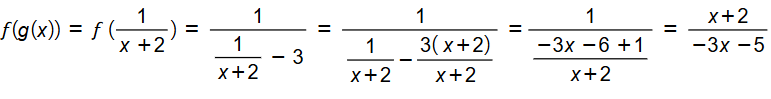
27 . تحد : إذا كان و كان فأحل المعادلة .
كتاب التمارين
أجد قيمة كل مما يأتي، مستعملا القيم المبينة في الجدولين الآتيين :
|
X |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
F(x) |
-7 |
-5 |
-3 |
-3 |
3 |
5 |
7 |
|
X |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
G(x) |
8 |
3 |
0 |
-1 |
0 |
3 |
8 |
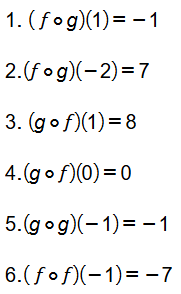
إذا كان f(x) = 2x+1 و g(x) = 3x-4 فأجد :
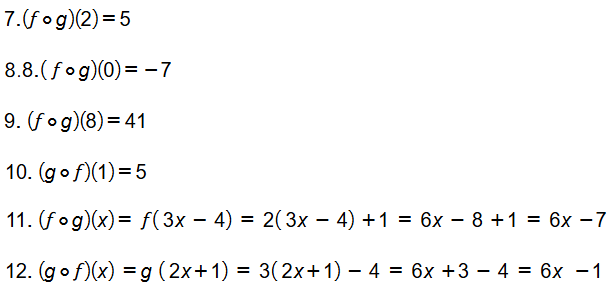
إذا كان و فأجد :
أجد اقترانين f(x) و g(x) بحيث يكون في كل مما يأتي:

23. يرتبط سعر سلعة معينة وعدد الوحدات المبيعة منها بالعلاقة ، ، حيث p السعر بالدينار، و x عدد الوحدات المبيعة. إذا كانت التكلفة C بالدنانير لإنتاج x وحدة هي ، فأجد التكلفة C في صورة اقتران نسبة إلى السعر p ، ثم أجد التكلفة إذا كان سعر الوحدة الواحدة 19 دينارا.
الحل