رياضيات فصل أول

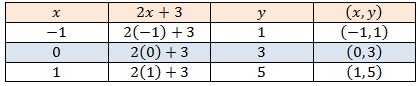
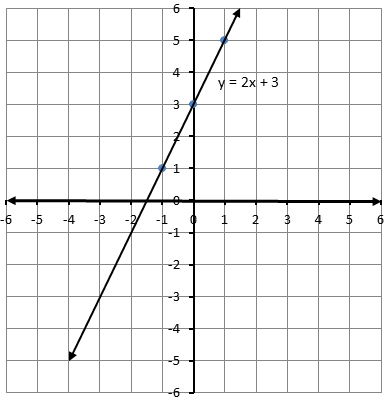
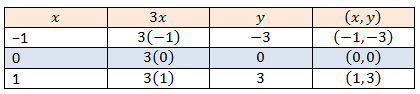
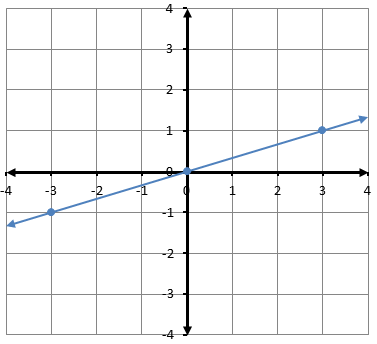
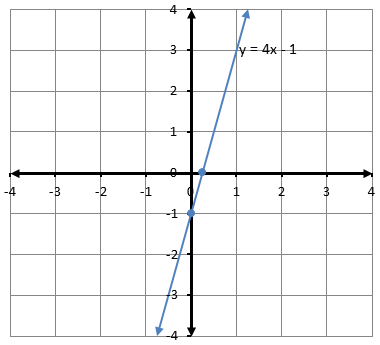
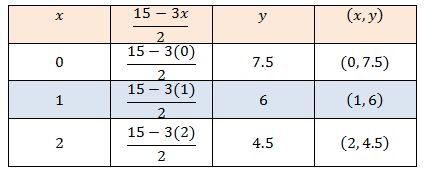أتحقق من فهمي(1)

أُحدّدُ ما إذا كانتْ كلُّ معادلةٍ ممّا يأتي خطّيّةً أَمْ لا، وإذا كانتْ كذلكَ أكتبُها على الصورةِ القياسيةِ

1) $2x=1-3y$

معادلة خطية والصورة القياسية لها هي $2x+3y=1$

2) $x^2-8y=3$

ليست معادلة خطية لأن $x$ مرفوعة للأس 2

3) $\frac{1}{5}y=2$

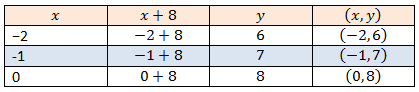
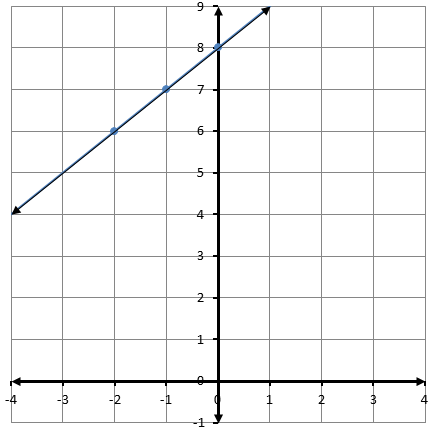
بضرب طرفي المعادلة بالعدد 5 يصبح شكلها $y=10$

وهذه معادلة خطية صورتها القياسية $0x+1y=10$

 

أتحقق من فهمي(2)

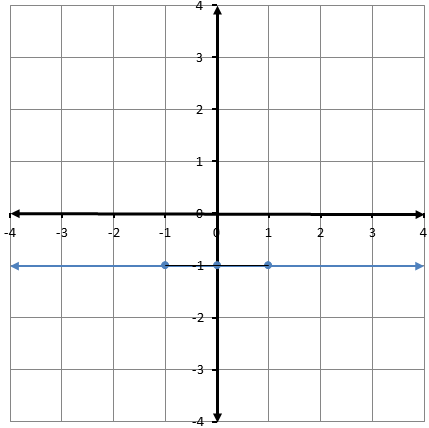
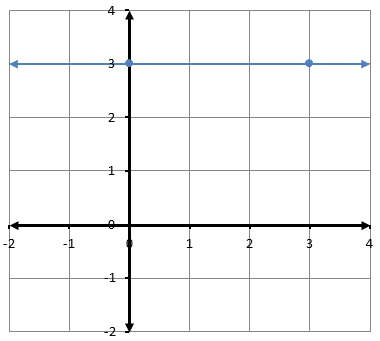
3) أمثِّلُ المعادلةَ 2y - 4x = 6 بيانيًّا.

$2y=4x+6$

$\frac{2y}{2}=\frac{4x}{2}+\frac{6}{2}$

$y= 2x+3$

 

 

2) أمثِّلُ المعادلةَ y = 3x بيانيًّا.

 

أتحقق من فهمي(3)

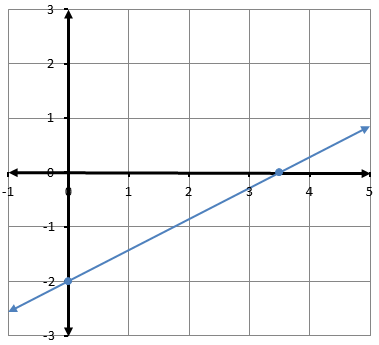
أمثّلُ كلَّ معادلةٍ ممّا يأتي بيانيًّا باستعمالِ المقطعِ x والمقطعِ :

1) $4x-y=1$

المقطع $x$:   $y=0\to 4x-0=1 \to x=0.25$

 

المقطع $y$:    $x=0 \to 4\left(0\right)-y=1\to y=-1$

 

2) $y = -7$ 

 

 

 

 

3) $x = 5$

 

أتحقق من فهمي(4)

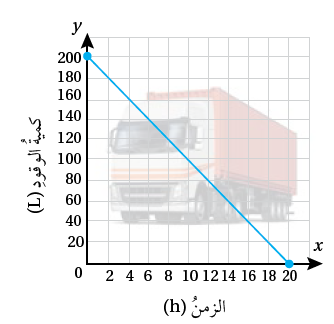
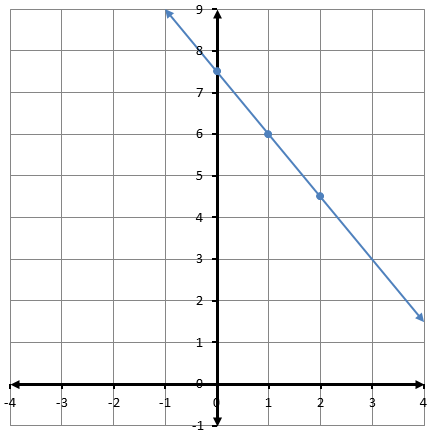
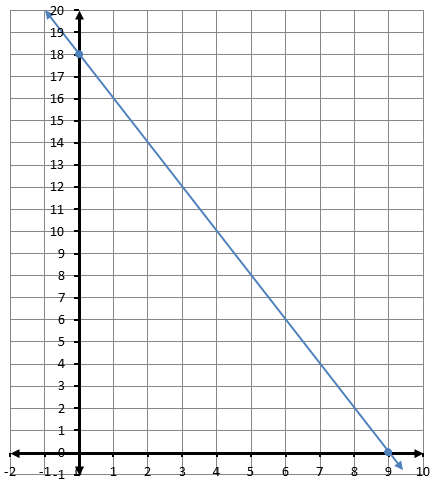
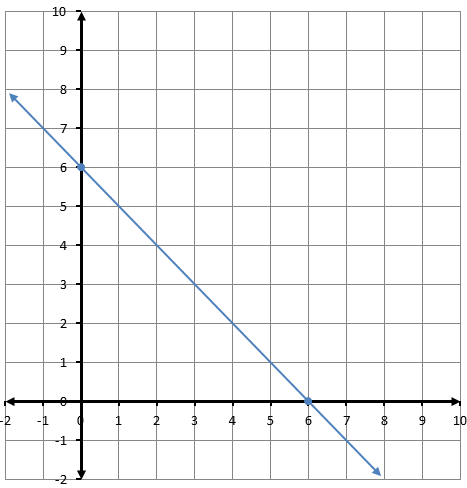
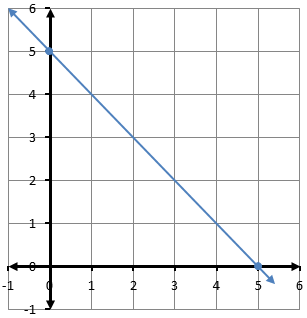
وقودٌ: يبينُ التمثيلُ البيانيُّ المجاورُ العلاقةَ بينَ عددِ لتراتِ 
الوقود المتبقية في خزانِ شاحنةٍ وعددِ ساعاتِ قيادتِها.

1) أجدُ المقطعَ x والمقطعَ y للعَلاقةِ.

المقطع $x$ يساوي 20 
المقطع $y$ يساوي 200

2) أصفُ مدلولَ كلٍّ منَ المقطعينِ في هذهِ الحالةِ.

المقطع $y$ يساوي 200 ويعني أنه يوجد 200 لتر وقود في الخزان عند بداية الحركة، المقطع $x$ يساوي 20، وهذا يعني أن الوقود نفد من الخزان بعد 20 ساعة. 

3) بعدَ كمْ ساعةِ قيادةٍ يبقى في خزانِ الشاحنةِ 100 L منَ الوقودِ؟

بعد 10 ساعات

 

أتدرب وأحل المسائل 

أحدّدُ ما إذا كانتْ كلُّ معادلةٍ ممّا يأتي خطّيّةً أم لا، وإذا كانتْ كذلكَ أكتبُها على الصورةِ القياسيةِ:

1) $2x = 7y \to 2x-7y=0$          معادلة خطية وصورتها القياسية

 

2)  $y= 1-x^2$               ليست خطية لأن $x$ مرفوعة للأس 2 

 

3) $9xy + 11x = 6$       ليست خطية لأن الحد $9xy$ فيه متغيران 

 

أمثّلُ كلَّ معادلةٍ ممّا يأتي بيانيًّا بإنشاءِ جدولِ قيمٍ:

 

4) $y=-1$ 

 

5) $y-x=8$

    $y=x+8$

 

6) $3x+2y=15$

 

    $y=\frac{15-3x}{2}$ 

 

أجدُ المقطعَ x والمقطعَ y لكلِّ معادلةٍ ممّا يأتي:

 المقطع $x$ يساوي $-2$ والمقطع $y$ يساوي 4 

 

 

 

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

 

المقطع $x$ يساوي 0 والمقطع $y$ يساوي 0

 

 

 

 

 

أمثّلُ كلَّ معادلةٍ ممّا يأتي بيانيًّا باستعمالِ المقطعِ $x$ والمقطعِ $x$:

9) $x = 4y-6$

 

المقطع $x$:     $y= 0 \to x=-6$  ،  المقطع $y$:    $x=0 \to y= 1.5$

 

10) $x+6=0$ 

المقطع $x$ هو $x=-6$، ولا يوجد مقطع $y$ فهو خط عامودي مستقيم 

 

11) $\frac{4x}{3}=\frac{3y}{4}+1$

المقطع $x$: $y=0\to x=\frac{3}{4}$    ،   المقطع $y$: $x=0\to y=\frac{-4}{3}$

 

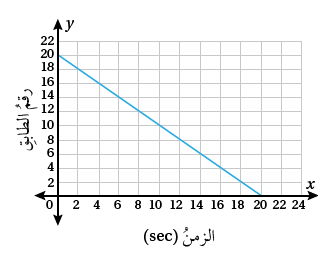
رحلةٌ: ملأَ رامي خزانَ سيارتِه بالوقودِ استعدادًا لرحلةٍ إلى مدينةِ العقبةِ. والمعادلةُ y = 18 - 2x تعطي كميّةَ الوقودِ باللتراتِ المتبقيةِ في خزانِ السيارةِ بعدَ قيادتِها x ساعةً.

12) أجدُ المقطعَ x والمقطعَ y للمعادلةِ المُعطاةِ، ثمَّ أستعملُ المقطعينِ لتمثيلِ المعادلةِ بيانيًّا.

المقطع $x$:  $x=9,y=0\to (9,0)$        

 المقطع $y$: $y=18,x=0\to (0, 18)$      

                                    

 

13) أصفُ مدلولَ كلٍّ منَ المقطعينِ في هذهِ الحالةِ.

كمية الوقود عند البدء هي قيمة المقطع $y$وتساوي 18 لتراً، وكمية الوقود تكفي ل 9 ساعات

 

14) بعدَ كمْ ساعةٍ منْ قيادةِ السيارةِ يتبقى $\frac{1}{4}$الوقود في الخزان؟ 

ربع الوقود يساوي 4.5 لتر    $$\begin{gathered} 4.5=18-2x \\ 2x=13.5 \\ x=6.75 \end{gathered}$$

يتبقى ربع الوقود بعد 6 ساعات و 45 دقيقة 

 

بنايةٌ: يبيّنُ التمثيلُ البيانيُّ المجاورُ العلاقةَ بينَ رقمِ الطابَقِ في أحدِ الأبراجِ التجاريةِ والزمنِ الذي يقضيهِ الراكبُ بالثواني في المِصْعدِ حتى يصلَ إلى هذا الطابقِ. فإذا علمتُ أنَّ رقمَ الطابقِ
الأرضيِّ 0، فأجيبُ عنْ كلٍّ ممّا يأتي: 

15) منْ أيِّ طابقٍ صعِدَ الراكبُ إلى المِصْعدِ؟ 

الطابق 20

16) بعدَ كمْ ثانيةٍ وصلَ الراكبُ إلى الطابَقِ
الأرضيِّ؟

بعد 20 ثانية

17) بعدَ كمْ ثانيةٍ وصلَ الراكبُ إلى الطابقِ
الثامنِ؟ 

بعد 12 ثانية

 

هندسةٌ: محيطُ المستطيلِ في الشكلِ المجاورِ 12 cm 

18) أكتبُ معادلةً بالصورةِ القياسيةِ تمثّلُ محيطَ المستطيلِ.

$2x+2y=12\to x+y=6$

 

19) أجدُ المقطعَ x والمقطعَ y للتمثيلِ البيانيِّ لمعادلةِ محيطِ
المستطيلِ. 

المقطع x يساوي 6، والمقطع y يساوي 6 

 

20) أمثّلُ المعادلةَ بيانيًّا.

21) أجدُ ثلاثةَ أزواجٍ مرتبةٍ تمثلُ أبعادَ المستطيلِ، على أنْ تكونَ قيمُ x و y أعدادًا كليّةً.

$(1, 5) , (2,4) , (3, 3)$

22) تحدٍّ: يبيّنُ التمثيلُ البيانيُّ المجاورُ المستقيمَ. $x + y = 5$

أرسمُ مستقيمًا على الصورةِ x = a ، ومستقيمًا على الصورةِ y = b ، على أنْ تكونَ المِساحةُ بينَ المستقيماتِ الثلاثةِ 4.5 وحداتٍ مربعةٍ. 

حل مقترح: يمكن ذلك عن طريق رسم المستقيمات $y=2 , x=0$

وهناك حلول أخرى: مثل رسم المستقيمين $y=0, x=2$ 

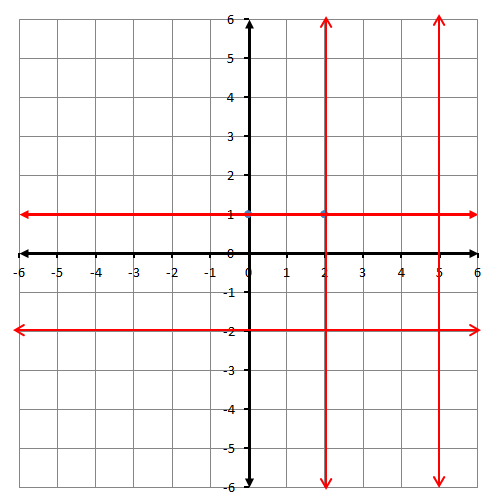
23) تبريرٌ: أمثّلُ المعادلاتِ x = 5, x = 2, y = -2, y = 1 في المستوى الإحداثيِّ نفسِه، ثمَّ أحدّدُ الشكلَ الهندسيَّ المغلقَ الناتجَ عنِ المستقيماتِ. أُبرّرُ إجابتِي.

الشكل المغلق الناتج هو مربع حيث أن طوله يساوي 3 وحدات وعرضه يساوي 3 وحدات 

 

 

 

 

 

 

 

 

 

24) أكتبُ: كيفَ أكتبُ معادلةً خطيّةً بالصورةِ القياسيةِ؟

أكتب المعادلة الخطية بالصورة القياسية بجعل كل من $x, y$ في جهة وفي الجهة الأخرى العدد الثابت وحتى تكون المعادلة بالصورة القياسية يجب أن يكون العامل المشترك الأكبر بين كل من المعاملات والعدد الثابت يساوي 1

 

كتاب التمارين 

أحددُ ما إذا كانَتْ كلُّ معادلةٍ ممّا يأتي خطيةً أَمْ لا، وإذا كانَتْ خطيةً فأكتبُها على الصورةِ القياسيةِ:

1) $\frac{1}{x}+\frac{1}{y}=8$         ليست معادلة خطية

 

2) $\frac{x}{3}=2+\frac{y}{5}$         معادلة خطية

$\frac{x}{3}-\frac{y}{5}=2\to 15*\left(\frac{x}{3}-\frac{y}{5}=2\right)$

$5x -3y=30$         الصورة القياسية

 

3) $\frac{5}{x}=y-1$        ليست معادلة خطية

 

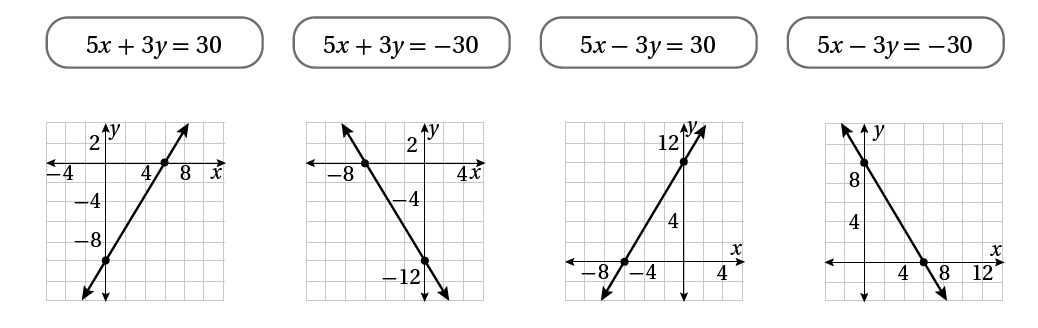
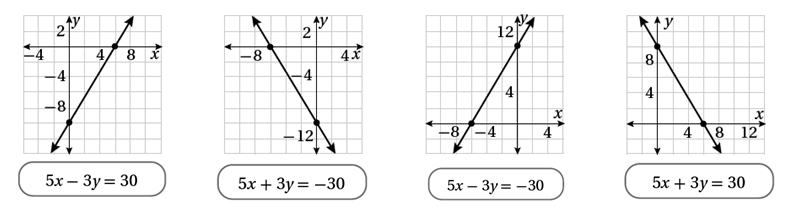
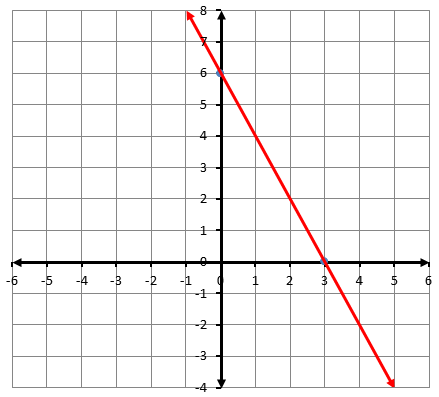
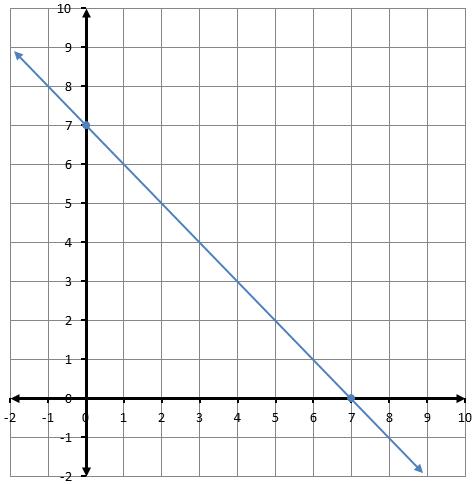
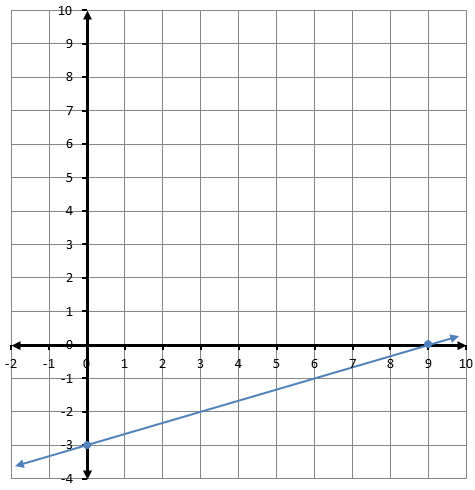
4) أصلُ بَيْنَ المعادلةِ والتمثيلِ البيانيِّ المناسبِ لَها:

الحل: 

أمثلُ كلَّ معادلةٍ ممّا يأتي بيانيًّا باستعمالِ المقطعِ x والمقطعِ y:

1) $\frac{1}{2}x+\frac{1}{4}y=\frac{3}{2}$

    $x=0 \Rightarrow \frac{1}{2}\left(0\right)+\frac{1}{4}y=\frac{3}{2}$

 

$4\times \left(\frac{1}{4}y=\frac{3}{2}\right)\Rightarrow y= 6 \Rightarrow (0, 6)$

 

$y=0 \Rightarrow \frac{1}{2}x+\frac{1}{4}\left(0\right)=\frac{3}{2}$

 

$2\times \left(\frac{1}{2}x=\frac{3}{2}\right)\Rightarrow x=3\Rightarrow (3, 0)$

 

 

 

2) $y = -x + 7$

$x= 0 \Rightarrow y=7\Rightarrow (0, 7)$

$y=0 \Rightarrow x=7\Rightarrow (7, 0)$ 

 

 

 

 

 

 

 

7) $y = 3x + 9$ 

$x=0 \Rightarrow y=9 \Rightarrow (0, 9)$

$y=0 \Rightarrow x=-3\Rightarrow (-3, 0)$

 

 

 

 

 

 

 

8) $1=10-3y$

$3y = 9\Rightarrow y= 3$ 

 

 

 

 

 

 

 

 

9) $4x-7y = 14$ 

$x=0 \Rightarrow y=-2 \Rightarrow (0, -2)$

$y=0 \Rightarrow x=3.5\Rightarrow (3.5, 0)$ 

 

 

 

 

 

 

10) $y = 5-x$ 

$x=0 \Rightarrow y=5 \Rightarrow (0, 5)$

$y=0 \Rightarrow x=5\Rightarrow (5, 0)$ 

 

 

 

 

 

 

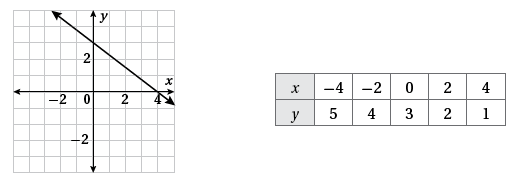
11) يمثلُ كلٌّ مِنَ التمثيلِ البيانيِّ والجدولِ الآتيَينِ معادلتَينِ مختلفتَينِ، بِمَ تتشابهُ المعادلتانِ وفيمَ تختلفانِ؟

تتشابهان بالمقطع $y$، وتختلفان بالمقطع $x$

 

12) أكتبُ معادلةً بالصورةِ القياسيةِ يكونُ المقطعُ x لتمثيلِها البيانيِّ 3 والمقطعُ y هُوَ 5

حل مقترح: 

$3y+5x=15$

13) أجدُ المقطعَينِ x وَ y للتمثيلِ البيانيِّ للمعادلةِ Ax + By = C

المقطع $x$:  $x=\frac{C}{A}$

المقطع $y$: $x=\frac{C}{B}$