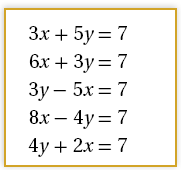رياضيات فصل أول

أتحقق من فهمي (1)

أكتبُ بصيغةِ الميلِ والمقطعِ معادلةَ المستقيمِ المارِّ بالنقطةِ $(-3, -1)$ والموازي للمستقيمِ
$y = 2x + 5$ .

1) المستقيمان المتوازيان لهما نفس الميل وعليه فميل كل من المستقيمين يساوي 2

2) بصيغة الميل والنقطة:

$y-y_1=m\left(x-x_1\right)$

$y-(-1)=2\left(x-(-1)\right)$

$y+1=2(x+1)$

 

3) نحول إلى صيغة الميل والمقطع:

$y+1=2x+2\Rightarrow y=2x+1$

 

أتحقق من فهمي (2)

أكتبُ بصيغةِ الميلِ والمقطعِ معادلةَ المستقيمِ المارِّ بالنقطةِ ( 8 , 1) والمُعامِدِ للمستقيمِ
$3y - 9x = 12$

1) ميل المستقيم المعطى

$3y - 9x=12$

$3y=9x+12\Rightarrow y=3x+4$

الميل يساوي 3

 

2) ميلَ المستقيمِ العموديِّ على المستقيمِ المُعْطى.

$m=\frac{-1}{3}$

 

3) معادلةَ المستقيمِ

$y-y_1=m\left(x-x_1\right)$

$y-8=\frac{-1}{3}\left(x-1\right)$

$y-8=\frac{-1}{3}x+\frac{1}{3}$

$y=\frac{-1}{3}x+\frac{25}{3}$

 

أتحقق من فهمي (3)

1) أحدّدُ ما إذا كانَ المستقيمانِ $2x + y = 7$ و $y - 2x = 3$ متوازيينِ أو متعامدينِ أو غيرَ ذلكَ.

أ) ميل المستقيم $2x + y = 7$

$y=-2x+7$

الميل يساوي $-2$

ب) ميل المستقيم $y - 2x = 3$

$y=2x+3$ 

الميل يساوي 2 

نلاحظ بأن الميلين غير متساويين لذا فهما غير متوازيين وأن حاصل ضربهما يساوي $-4$ وليس $-1$ لذا فهما غير متعامدين أيضاً

 

2) أحدّدُ ما إذا كانَ $\overleftrightarrow{AB}$ و $\overleftrightarrow{CD}$ متوازيينِ أو متعامدينِ أو غيرَ ذلكَ، حيثُ $\mathit{A}\mathbf{(}\mathbf{3}\mathbf{,}\mathbf{ }\mathbf{6}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{B}\mathbf{(}\mathbf{-}\mathbf{9}\mathbf{,}\mathbf{ }\mathbf{2}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{C}\mathbf{(}\mathbf{5}\mathbf{,}\mathbf{ }\mathbf{4}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{D}\mathbf{(}\mathbf{2}\mathbf{,}\mathbf{ }\mathbf{3}\mathbf{)}$

أ) ميل $\overleftrightarrow{AB }$

$m=\frac{y_2-y_1}{x_2-x_1}$

$m=\frac{2-6}{-9-3}=\frac{-4}{-12}=\frac{1}{3}$

 

ب) ميل $\overleftrightarrow{CD}$

$m=\frac{y_2-y_1}{x_2-x_1}$

$m=\frac{3-4}{2-5}=\frac{-1}{-3}=\frac{1}{3}$

نلاحظ بأن الميل متساوي لذا فهما متوازيين

 

أتحقق من فهمي (4)

في المثالِ السابقِ، تخطّطُ البلديةُ لإنشاءِ مسارِ ركضٍ آخرَ داخلَ الحديقةِ موازٍ لمسارِ الركضِ الأولِ ويمرُّ في مَدخلِ الحديقةِ. أجدُ معادلةَ المستقيمِ الذي يمثلُ مسارَ الركضِ الجديدَ.

من المثال أوجدنا أن ميل مسار الركض يساوي 2 

وبما أن المسار الجديد يمر بمدخل الحديقة والذي يمثل النقطة $(0, 4)$، فإن المعادلة تكون: 

$y=2x+4$

 

أتدرب وأحل المسائل

أكتبُ بصيغةِ الميلِ والمقطعِ معادلةَ المستقيمِ المارِّ بالنقطةِ المُعْطاةِ والموازي للمستقيم المُعْطاةِ معادلتُه في كلٍّ ممّا يأتي:

$\mathbf{1}\mathbf{)}\mathbf{ }\mathbf{(}\mathbf{-}\mathbf{1}\mathbf{,}\mathbf{ }\mathbf{5}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{y}\mathbf{=}\frac{\mathbf{1}}{\mathbf{2}}\mathbf{(}\mathit{x}\mathbf{-}\mathbf{10}\mathbf{)}$

$m=\frac{1}{2}$

$y-5=\frac{1}{2}(x+1)$

$y-5=\frac{1}{2}x+\frac{1}{2}\Rightarrow y=\frac{1}{2}x+5.5$

 

 

$\mathbf{2}\mathbf{)}\mathbf{ }\mathbf{(}\mathbf{2}\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{7}\mathbf{)}\mathbf{,}\mathbf{ }\mathbf{2}\mathit{y}\mathbf{=}\mathbf{5}\mathit{x}\mathbf{-}\mathbf{3}$

 

$y=\frac{5}{2}x-\frac{3}{2},m=\frac{5}{2}$

$y+7=\frac{5}{2}(x-2)$

$y+7=\frac{5}{2}x-5\Rightarrow y=\frac{5}{2}x-12$

 

 

$\mathbf{3}\mathbf{)}\mathbf{ }\mathbf{(}\mathbf{4}\mathbf{,}\mathbf{ }\mathbf{8}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{x}\mathbf{+}\mathbf{4}\mathit{y}\mathbf{-}\mathbf{9}\mathbf{=}\mathbf{0}$

 

$4y=-x+9$

$y=\frac{-1}{4}x+\frac{9}{4},m=\frac{-1}{4}$

$y-8=\frac{-1}{4}(x-4)$

$y-8=\frac{-1}{4}x+1\Rightarrow y=\frac{-1}{4}x+9$

 

 

$\mathbf{4}\mathbf{)}\mathbf{ }\mathbf{(}\mathbf{9}\mathbf{,}\mathbf{ }\mathbf{3}\mathbf{)}\mathbf{,}\mathbf{ }\mathbf{2}\mathit{x}\mathbf{-}\mathbf{7}\mathit{y}\mathbf{+}\mathbf{1}\mathbf{=}\mathbf{0}$

 

$7y=2x+1$

$y=\frac{2}{7}x+\frac{1}{7},m=\frac{2}{7}$

$y-3=\frac{2}{7}(x-9)$

$y-3=\frac{2}{7}x-\frac{18}{7}\Rightarrow y=\frac{2}{7}x+\frac{3}{7}$

 

أكتبُ بصيغةِ الميلِ والمقطعِ معادلةَ المستقيمِ المارِّ بالنقطةِ المُعطاةِ والمُعامِدِ للمستقيمِ المُعْطاةِ معادلتُه في كلٍّ ممّا يأتي:

$\mathbf{5}\mathbf{)}\mathbf{ }\mathbf{(}\mathbf{2}\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{7}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{y}\mathbf{=}\mathit{x}\mathbf{-}\mathbf{2}$

$m=\frac{-1}{1}=-1$

$y+7=-1(x-2)$

$y+7=-x+2\Rightarrow y=-x-5$

 

$\mathbf{6}\mathbf{)}\mathbf{ }\mathbf{(}\mathbf{-}\mathbf{5}\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{4}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{y}\mathbf{=}\frac{\mathbf{1}}{\mathbf{2}}\mathit{x}\mathbf{+}\mathbf{1}$

$m=\frac{-1}{{\displaystyle \frac{1}{2}}}=-2$

$y+4=-2(x+5)$

$y+4=-2x-10\Rightarrow y=-2x-14$

 

 

$\mathbf{7}\mathbf{)}\mathbf{ }\mathbf{(}\mathbf{2}\mathbf{,}\mathbf{ }\mathbf{2}\mathbf{)}\mathbf{,}\mathbf{ }\mathbf{3}\mathit{y}\mathbf{=}\mathbf{-}\mathbf{2}\mathit{x}\mathbf{+}\mathbf{6}$

$y=\frac{-2}{3}x+2$

$m=\frac{-1}{{\displaystyle \frac{-2}{3}}}=\frac{3}{2}$

$y-2=\frac{3}{2}(x-2)$

$y-2=\frac{3}{2}x-3\Rightarrow y=\frac{3}{2}x-1$

 

$\mathbf{8}\mathbf{)}\mathbf{ }\mathbf{(}\mathbf{-}\mathbf{3}\mathbf{,}\mathbf{ }\mathbf{0}\mathbf{)}\mathbf{,}\mathbf{ }\mathbf{3}\mathit{x}\mathbf{-}\mathbf{4}\mathit{y}\mathbf{=}\mathbf{-}\mathbf{4}$

$4y=3x+4$

$$\begin{gathered} y=\frac{3}{4}x+1 \\ m=\frac{-4}{3} \end{gathered}$$

$y-0=\frac{-4}{3}(x+3)\Rightarrow y=\frac{-4}{3}x-4$

 

يبيّنُ الشكلُ المجاورُ التمثيلَ البيانيَّ للمستقيمِ الذي معادلتُه $y + 2x = 6$

9) أُبيّنُ أنَّ النقطةَ $(1, 4)$ تقعُ على المستقيمِ

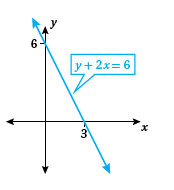
نعوض النقطة بالمستقيم 

$$\begin{gathered} 4+2\left(1\right)=6 \\ 4+2=6 \\ 6=6 \end{gathered}$$

إذن النقطة تقع على المستقيم

10) أجد ميل المستقيم 

$y=-2x+6$

الميل يساوي $-2$

11) أكتبُ معادلةَ المستقيمِ بصيغةِ الميلِ ونقطةٍ.

$y-0=-2(x-3)$

12) أجدُ معادلةَ المستقيمِ المارِّ بنقطةِ الأصلِ والموازي للمستقيمِ المُعطى بصيغةِ الميلِ والمقطعِ.

$$\begin{gathered} m=-2 \\ y=-2x \end{gathered}$$

 

13) يحتوي الصندوقُ المجاورُ على زوجينِ منَ المستقيماتِ المتعامدةِ. فأيُّ المستقيماتِ مختلفٌ؟ أبرّرُ إجابتِي. 

$3x+5y=7 \Rightarrow y=\frac{-3}{5}x+\frac{7}{5} \Rightarrow m=\frac{-3}{5}$

$3y-5x=7\Rightarrow y=\frac{5}{3}x+\frac{7}{3}\Rightarrow m=\frac{5}{3}$

$\frac{-3}{5}\times \frac{5}{3}=-1$

إذن فالمستقيمان متعامدان 

 

$8x-4y=7\Rightarrow y=2x-\frac{7}{4}\Rightarrow m=2$

$4y+2x=7\Rightarrow y=\frac{-1}{2}x+7\Rightarrow m=\frac{-1}{2}$

$2\times \frac{-1}{2}=-1$

إذن فالمستقيمان متعامدان 

$6x+3y=7\Rightarrow y=-2x+\frac{7}{6}\Rightarrow m=-2$

وعليه فهو المستقيم المختلف ولا يعامد أي من المستقيمات السابقة

 

 أحدّدُ ما إذا كانَ المستقيمانِ $\overleftrightarrow{AB}$ و $\overleftrightarrow{CD }$ متوازيينِ أو متعامدينِ أو غيرَ ذلك في كلٍّ ممّا يأتي:

$\mathbf{14}\mathbf{)}\mathbf{ }\mathit{A}\mathbf{(}\mathbf{8}\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{2}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{B}\mathbf{(}\mathbf{4}\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{1}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{C}\mathbf{(}\mathbf{3}\mathbf{,}\mathbf{ }\mathbf{11}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{D}\mathbf{(}\mathbf{-}\mathbf{2}\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{9}\mathbf{)}$

$\overleftrightarrow{AB}:$

$m=\frac{-1-(-2)}{4-8}=-\frac{1}{4}$

 

$\overleftrightarrow{CD:}$

$m=\frac{-9-11}{-2-3}=\frac{-20}{-5}=4$

$-\frac{1}{4}\times 4=-1$

وعليه فالمستقيمان متعامدان

 

$\mathbf{15}\mathbf{)}\mathbf{ }\mathit{A}\mathbf{(}\mathbf{8}\mathbf{,}\mathbf{ }\mathbf{4}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{B}\mathbf{(}\mathbf{4}\mathbf{,}\mathbf{3}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{C}\mathbf{(}\mathbf{4}\mathbf{,}\mathbf{-}\mathbf{9}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{D}\mathbf{(}\mathbf{2}\mathbf{,}\mathbf{-}\mathbf{1}\mathbf{)}\mathbf{ }$

$\overleftrightarrow{AB}:$

$m=\frac{3-4}{4-8}=\frac{1}{4}$

 

$\overleftrightarrow{CD:}$

$m=\frac{-1-(-9)}{2-4}=\frac{8}{-2}=-4$

$\frac{1}{4}\times -4=-1$

وعليه فالمستقيمان متعامدان

 

$\mathbf{16}\mathbf{)}\mathbf{ }\mathit{A}\mathbf{(}\mathbf{1}\mathbf{,}\mathbf{ }\mathbf{5}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{B}\mathbf{(}\mathbf{4}\mathbf{,}\mathbf{ }\mathbf{4}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{C}\mathbf{(}\mathbf{9}\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{1}\mathbf{)}\mathbf{,}\mathbf{ }\mathbf{(}\mathbf{-}\mathbf{6}\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{5}\mathbf{)}\mathbf{ }$

$\overleftrightarrow{AB}:$

$m=\frac{4-5}{4-1}=-\frac{1}{3}$

$\overleftrightarrow{CD:}$

$m=\frac{-5-(-1)}{-6-9}=\frac{-4}{-15}=\frac{4}{15}$

وعليه فالمستقيمان غير متوازيين وغير متعامدين

 

$\mathbf{17}\mathbf{)}\mathbf{ }\mathit{A}\mathbf{(}\mathbf{4}\mathbf{,}\mathbf{ }\mathbf{2}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{B}\mathbf{(}\mathbf{-}\mathbf{3}\mathbf{,}\mathbf{ }\mathbf{1}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{C}\mathbf{(}\mathbf{6}\mathbf{,}\mathbf{ }\mathbf{0}\mathbf{)}\mathbf{,}\mathbf{ }\mathit{D}\mathbf{(}\mathbf{-}\mathbf{10}\mathbf{,}\mathbf{ }\mathbf{8}\mathbf{)}$

$\overleftrightarrow{AB}:$

$m=\frac{1-2}{-3-4}=\frac{1}{7}$

$\overleftrightarrow{CD:}$

$m=\frac{8-0}{-10-6}=\frac{8}{-16}=\frac{-1}{2}$

وعليه فالمستقيمان غير متوازيين وغير متعامدين

 

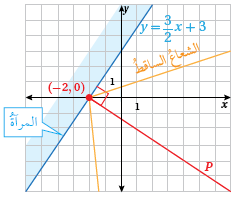
18) تمثل المعادلة $y=\frac{3}{2}x+3$، سطح مرآةٍ، وتمثّلُ النقطةُ ( 0 , 2-) نقطةَ التقاءِ الشعاعِ الساقطِ معَ المرآةِ. أجدُ معادلةَ العمودِ المُقامِ على المرآةِ $P$. 

$m=\frac{-1}{{\displaystyle \frac{3}{2}}}=\frac{-2}{3}$

$y-0=\frac{-2}{3}(x+2)\Rightarrow y=\frac{-2}{3}x-\frac{4}{3}$

 

 

 

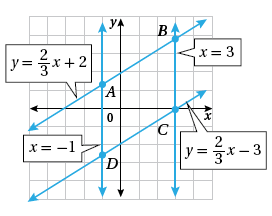
19) أستعملُ الميلَ لتحديدِ ما إذا كانَ الشكلُ 
الرباعيُّ ABCD المُبيَّنُ في التمثيلِ البيانيِّ المجاورِ
يمثلُ متوازيَ أضلاعٍ.

$AB:m=\frac{2}{3}$

$CD:m=\frac{2}{3}$

AB يوازي CD 

المستقيمان $x=-1, x=3$ متوازيان أيضاً 

إذن الشكل الرباعي يمثل متوازي أضلاع 

 

تبريرٌ: تمثلُ النقاطُ ( 1, A(5, 10), B(1, 5), C(6 ثلاثةَ رؤوسٍ لمتوازي الأضلاعِ ABCD

20) أجدُ معادلة المستقيمِ المارِّ بالنقطتينِ A و C

$m=\frac{1-10}{6-5}=-9\Rightarrow y-1=-9(x-6)$

 

21) أجدُ إحداثيَّيْ نقطتينِ مُحْتمَلتينِ للرأسِ الرابعِ D لمتوازي الأضلاعِ، مبرّرًا إجابتِي.

نفترض إحداثيات الرأس الرابع $D(x, y)$ 

$\Leftarrow$المستقيم المار بالنقطتين C , D موازي للمستقيم المار بالنقطتين A , B 

ميل المستقيم AB: 

$m=\frac{5-10}{1-5}=\frac{-5}{-4}=\frac{5}{4}$

وبما أن المستقيمين لهما نفس الميل:

$m=\frac{y-1}{x-6}$

$\frac{5}{4}=\frac{y-1}{x-6}\Rightarrow 5x-30=4y-4$

ومن هنا هناك حالتان:

1) أن يتشكل المستقيم BD الموازي للمستقيم AC الذي ميله يساوي $-9$ من الفرع السابق

             $m=\frac{y-5}{x-1}$

             $-9=\frac{y-5}{x-1}$

    ومنه:  $-9x+9=y-5$

             $y=-9x+14$

وبتعويض المعادلة الناتجة بالمعادلة السابقة: 

$5x-30=4(-9x+14)-4$

$5x-30=-36x+56-4$

$41x=82\Rightarrow x=2$

$y=-9*2+14\Rightarrow y=-4$

$D(2, -4)$

 

 

2) أن يتشكل المستقيم AD الموازي للمستقيم BC

ميل BC:

$m=\frac{1-5}{6-1}=\frac{-4}{5}$

ومنه: $m=\frac{y-10}{x-5}$

      $\frac{-4}{5}=\frac{y-10}{x-5}$

  $-4x+20=5y-50$

بضرب المعادلة الأولى ب 4 والثانية ب 5 ثم جمع المعادلتين:

         

 

 

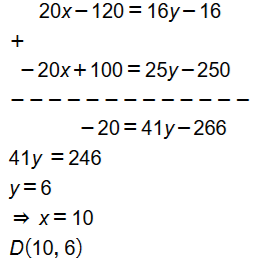
22) تبريرٌ: يبيّنُ الشكلُ المجاورُ التمثيلَ البيانيَّ 
لمستقيمينِ متوازيينِ في المستوى الإحداثيِّ.
أجدُ معادلةَ المستقيمِ السُّفْليِّ، وأبرّرُ إجابتِي.

المستقيمان متوازيان وميلهما يساوي $\frac{2}{3}$

مقطع المستقيم العلوي $(0, 4)$

مقطع المستقيم السفلي $(0, -3)$ 

$y=\frac{2}{3}x-3$

 

23) تحدٍّ: أجدُ قيمةَ a التي تجعلُ المستقيمينِ $y=ax + 5 و 2y=(a+4)x-1$ متوازيينِ

$a=\frac{a+4}{2}\Rightarrow 2a=a+4\Rightarrow a=4$

 

24) أكتبُُ كيفَ يمكنُ تحديدُ ما إذا كانَ مستقيمانِ في المستوى الإحداثيِّ متوازيينِ أو متعامِدينِ أو غيرَ ذلك؟

نجد الميل للمستقيمين: 

الميل متساوي $\Leftarrow$  المستقيمان متوازيان

حاصل ضرب ميلهما $-1$ $\Leftarrow$  المستقيمان متعامدون 

لم يحقق أي من الشرطين $\Leftarrow$ غير ذلك

 

كتاب التمارين

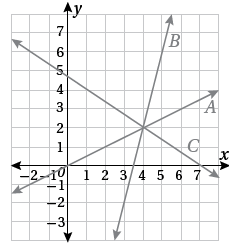
يبيّنُ الشكلُ المجاورُ التمثيلَ البيانيَّ للمستقيماتِ A وَ B وَ C ، أجدُ:

1) ميلَ مستقيمٍ معامدٍ للمستقيمِ A

نأخذ نقطتين يمر بهما المستقيم A، ولتكن:

$\left(0, 0\right), (4, 2)$

$m=\frac{2-0}{4-0}=\frac{1}{2}$

ميل مستقيم معامد يساوي $-2$

 

 

2) ميلَ مستقيمٍ موازٍ للمستقيمِ C

$(7, 0), (4, 2)$

$m=\frac{2-0}{4-7}=\frac{-2}{3}$

 

3 معادلةَ المستقيمِ المعامدِ للمستقيمِ B وَالمارِّ في نقطةِ تقاطعِ المستقيماتِ الثلاثةِ.

$(4, 2), (5, 6)$

$m=\frac{6-2}{5-4}=4$

ميل مستقيم معامد يساوي $\frac{-1}{4}$

معادلة المستقيم: $y-2 =\frac{-1}{4}(x-4)$

 

4) أكتبُ معادلةَ المستقيمِ المارِّ بالنقطةِ ( 7 , 4) والموازي للمستقيمِ $\overleftrightarrow{AB}$ ، حيثُ $B(5, 2) , A(1, 4)$
$m=\frac{4-2}{1-5}=\frac{2}{-4}=\frac{-1}{2}$

$y-7=\frac{-1}{2}(x-4)$

 

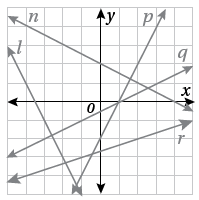
أسمّي مستقيماتٍ مِنَ الشكلِ المجاورِ تطابقُ الوصفَ في كلٍّ ممّا يأتي: 

5) مستقيمٌ موازٍ للمستقيمِ الّذي معادلتُهُ $y = 2x-3$

المستقيم $p$ حيث ميله يساوي 2

6) مستقيمٌ عموديٌّ على المستقيمِ الّذي معادلتُهُ $y=\frac{1}{2}x+7$

المستقيم $L$ حيث ميله يساوي $-2$

 

 

7) تبريرٌ: أبيّنُ ما إذا كانَ المستقيمانِ $7x - 3y = 5$ وَ $7x - 3y = 8$ متوازيَينِ أَمْ لا مِنْ دونِ إيجادِ الميلِ.

المستقيمان متوازيان لأن كل من a و b متساويان في المعادلتين والاختلاف في قيمة c

 

 

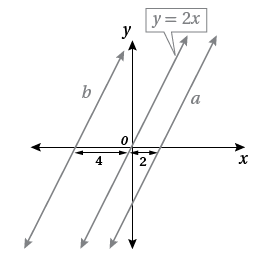
تبريرٌ: يبيّنُ التمثيلُ البيانيُّ المجاورُ ثلاثةَ مستقيماتٍ متوازيةٍ. أجدُ معادلةَ كلٍّ مِنَ المستقيمَينِ a وَ b. أبرّرُ إجابتي. 

المستقيم a: $y=2x-4$

لأنه يمر بالنقطة $(2, 0)$

المستقيم b: $y=2x+8$

لأنه يمر بالنقطة $(-4, 0)$