التوزيع الطبيعي

Normal Distribution

سنتعرف في درس التوزيع الطبيعي إلى:

1- منحنى التوزيع الطبيعي، وخصائصه.

2- إيجاد احتمالات المُتغيَّر العشوائي الطبيعي باستعمال القاعدة التجريبية.

3- المتغير العشوائي الطبيعي، والتوزيع الطبيعي.

 

تعلمت سابقًا أنَّ البيانات العددية التي تجمع عن ظاهرة معينة يمكن رصدها في صورة أعداد، ويمكن قياسها وإجراء العمليات الحسابية عليها، وترتيبها تصاعديًا وتنازليًا.

 

يتم تصنيف البيانات العددية إلى نوعين هما:

• بيانات منفصلة: وهي البيانات القابلة للعد مثل عدد الأشخاص، عدد الكتب، عدد الأجهزة،....
• بيانات متصلة: وهي البيانات الغير قابلة للعد مثل الطول، الكتلة، السرعة، ...

 

وتعلمت سابقًا أن البيانات العددية تُمثَّل بيانيًا باستعمال المخططات التكرارية.

إذا كان تمثيل البيانات لتوزيع ما يُعطي الشكل الآتي:

 

 

فإن التوزيع يسمى بالتوزيع الطبيعي ويسمى المنحنى منحنى التوزيع الطبيعي.

 

خصائص منحنى التوزيع الطبيعي

• منحنى متصل له شكل الجرس.
• تطابق الوسط الحسابي والوسيط والمنوال، وتوسط كُلٍّ منهما البيانات.
• تماثل البيانات حول الوسط الحسابي.
• اقتراب المنحنى عند طرفيه من المحور $x$ من دون أنْ يمسَّه.
• المساحة الكلية أسفل المنحنى تساوي 1.

 

يرمز للوسط الحسابي بالرمز $\mu$

يرمز للانحراف المعياري بالرمز $\sigma$

***تُمثِّل المساحة التي تقع بين قيمتين من البيانات أسفل المنحنى الطبيعي النسبة المئوية للبيانات.

 

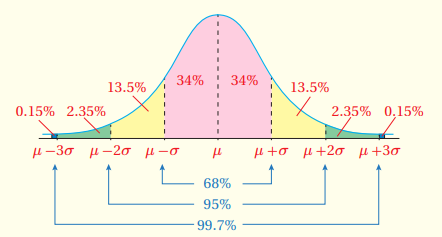
القاعدة التجريبية

مفهوم أساسي

إذا اتخذت مجموعة من البيانات شكل المنحنى الطبيعي، وكان وسطها الحسابي $\mu$، وانحرفها المعياري $\sigma$، فإنَّ:

 

• $68\%$ من المشاهدات تقريبًا تقع بين $\mu +\sigma و \mu -\sigma$؛ أيْ إنَّ $68\%$ من البيانات لا يزيد البُعْد بينها وبين الوسط الحسابي على قيمة الانحراف المعياري.
• $95\%$ من المشاهدات تقريبًا تقع بين $\mu +2\sigma و \mu -2\sigma$؛ أيْ إنَّ $95\%$ من البيانات لا يزيد البُعْد بينها وبين الوسط الحسابي على مثلي قيمة الانحراف المعياري.
• $99.7\%$  من المشاهدات تقريبًا تقع بين $\mu +3\sigma و \mu -3\sigma$؛ أيْ إنَّ $99.7\%$ من البيانات لا يزيد البُعْد بينها وبين الوسط الحسابي على ثلاثة أمثال قيمة الانحراف المعياري.

 

مثال 1: إذا اتخذت مجموعة علامات طلبة الصف العاشر في مادة الرياضيات شكل منحنى التوزيع الطبيعي، فأجد كُلاٍّ ممّا يأتي:

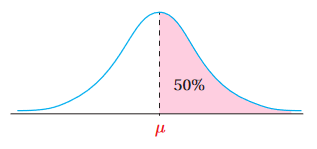
1) النسبة المئوية للطلبة الذين تقع علاماتهم فوق الوسط الحسابي.

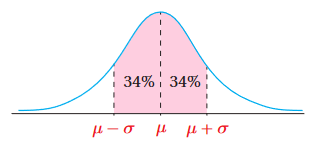
2) النسبة المئوية للطلبة الذين لا يزيد البُعْد بين علاماتهم والوسط الحسابي على انحراف معياري واحد.

3) النسبة المئوية للطلبة الذين تقل علاماتهم عن الوسط الحسابي بمقدار لا يزيد عن انحرافين معياريين.

4)النسبة المئوية للطلبة الذين تزيد  علاماتهم على الوسط الحسابي بمقدار لا يزيد عن انحرافين معياريين، أو تقلُّ عنه بمقدار  لا يزيد على انحراف معياري واحد.

الحل: 

بإستعمال القاعدة التجريبية

1) كما هو موضح بالشكل المجاور،

فإن النسبة المئوية للطلبة الذين تقع علاماتهم فوق الوسط الحسابي هي: $50\%$، لأن النسبة المئوية لجميع الطلبة الذين تقع علاماتهم تحت المنحنى الطبيعي هي: $100\%$، والمنحنى متماثل حول الوسط الحسابي؛أيْ أنَّ النسبة المئوية فوق الوسط = النسبة المئوية تحت الوسط = $50\%$ .  

2) كما هو موضح بالشكل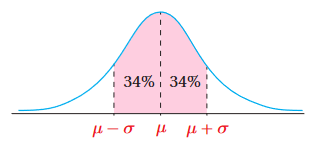 المجاور،

فإن النسبة المئوية للطلبة الذين لا يزيد البُعْد بين علاماتهم والوسط الحسابي على انحراف معياري واحد  $\mu +\sigma و \mu -\sigma$ هي: $68\%$.  

3) كما هو موضح بالشكل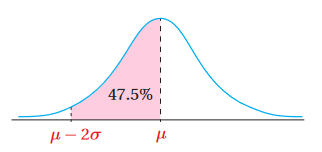 المجاور، فإن النسبة المئوية للطلبة الذين تقل  علاماتهم عن الوسط الحسابي بمقدار لا يزيد عن انحرافين معياريين

$\mu -2\sigma$ هي: $47.5\%$.

4) كما هو موضح بالشكل 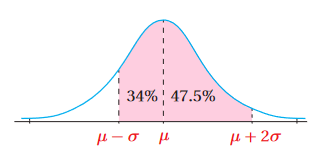المجاور،  فإن النسبة المئوية للطلبة الذين تزيد  علاماتهم على الوسط الحسابي بمقدار لا يزيد عن انحرافين معياريين        $\mu +2\sigma$، أو تقلُّ عنه بمقدار  لا يزيد على انحراف معياري واحد $\mu -\sigma$ هي: $81.5\%$ لأن:

$47.5\%+34\%=81.5\%$ .

 

مثال2: إذا اتخذت كتل مجموعة من طلبة الصف الثاني عشر  شكل المنحنى الطبيعي، فأجد كُلاٍّ ممّا يأتي:

1)النسبة المئوية للطلبة الذين تقع كتلهم فوق الوسط الحسابي.

2)النسبة المئوية للطلبة الذين لا يزيد البُعْد بين كتلهم والوسط الحسابي على انحراف معياري واحد.

3)النسبة المئوية للطلبة الذين تقل  كتلهم عن الوسط الحسابي بمقدار لا يزيد عن انحرافين معياريين.

4)النسبة المئوية للطلبة الذين تزيد  كتلهم على الوسط الحسابي بمقدار لا يزيد عن انحرافين معياريين، أو تقلُّ عنه بمقدار  لا يزيد على انحراف معياري واحد.

الحل:

 بإستعمال القاعدة التجريبية

1) كما هو موضح بالشكل المجاور،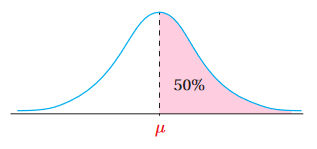 فإن النسبة المئوية للطلبة الذين تقع كتلهم فوق الوسط الحسابي $50\%$، لأن النسبة المئوية لجميع الطلبة الذين تقع كتلهم تحت المنحنى الطبيعي هي:$100\%$ والمنحنى متماثل حول الوسط الحسابي؛أيْ أنَّ النسبة المئوية فوق الوسط = النسبة المئوية تحت الوسط = $50\%$.

2) كما هو موضح بالشكل المجاور،

فإن النسبة المئوية للطلبة الذين لا يزيد البُعْد بين كتلهم والوسط الحسابي على انحراف معياري واحد $\mu +\sigma و \mu -\sigma$ هي: $68\%$.

3) كما هو موضح بالشكل المجاور،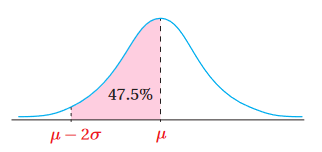 فإن النسبة المئوية للطلبة الذين تقل  كتلهم عن الوسط الحسابي بمقدار لا يزيد عن انحرافين معياريين $\mu -2\sigma$هي: $47.5\%$. 

4) كما هو موضح بالشكل المجاور،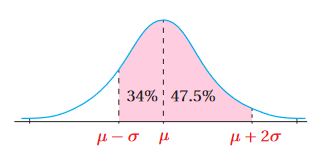 فإن النسبة المئوية للطلبة الذين تزيد  كتلهم على الوسط الحسابي بمقدار لا يزيد عن انحرافين معياريين $\mu +2\sigma$، أو تقلُّ عنه بمقدار لا يزيد على انحراف معياري واحد $\mu -\sigma$هي: $81.5\%$ لأن:

 $47.5\%+34\%=81.5\%$.

 

أتحقق من فهمي

إذا اتخذ التمثيل البياني لأطوال مجموعة من طلبة الصف العاشر شكل المنحنى الطبيعي، فأجد كُلاً ممّا يأتي:

1) النسبة المئوية للطلبة الذين تقع أطوالهم تحت الوسط الحسابي.

الإجابة:$50\%$

2) النسبة المئوية للطلبة الذين لا يزيد البُعْد بين أطوالهم والوسط الحسابي على انحرافين معياريين.

الإجابة: $95\%$

3) النسبة المئوية للطلبة الذين تزيد أطوالهم عن الوسط الحسابي بمقدار  لا يزيد عن انحرافين معياريين.

الإجابة:$47.5\%$

4) النسبة المئوية للطلبة الذين تقلَّ أطوالهم عن الوسط الحسابي بمقدار  لا يزيد على ثلاثة  انحرافات معياريه، أو تزيد عليه بمقدار لا يزيد عن انحرافين. معياريين.

 الإجابة: $49.85\%+47.5\%=97.35\%$

 

مفهوم أساسي

• المُتغيِّر العشوائي المنفصل: هو متغير عشوائي يأخذ قيمًا معدودة.

أمثلة:

• عدد الطلبة الذين تقل علاماتهم عن 70 في امتحان علامته القصوى 100.
•  عدد الطلبة في الصف الثاني  عاشر الذين أطوالهم أقل من 155cm.
• عدد الأطفال في كل أسرة في مدينة معينة.
•  عدد المصابيح الكهربائية التي ينتجها مصنع خلال زمن معين.

 

 

• المُتغيِّر العشوائي المتصل: هو متغير عشوائي يأخذ قيمًا متصلة ضمن فترة مُعيَّنة من الأعدد الحقيقية.

​​​​أمثلة:

• سرعة أول سيارة ستمرُّ أمام إحدى الحدائق خلال الساعة القادمة. 
• كتل الطلبة في مدرسة معينة.
• معدل هطول الأمطار على مدار عام في مدينة معينة.

 

*** إذا ارتبط المُتغيِّر العشوائي المتصل $X$ بتجربة عشوائية، وكان شكل تمثيلها البياني هو شكل المنحنى الطبيعي، فإن المُتغيِّر العشوائي  $X$ يسمى مُتغيِّرًا عشوائيًا طبيعيًا، ويسمى توزيعه الاحتمالي التوزيع الطبيعي $(normal distribution)$، ويمكن التعبير عنه بالرموز على النحو الآتي:$X~N(\mu , {\sigma }^2)$

حيث:

$\mu$: الوسط الحسابي

${\sigma }_{}$:الانحراف المعياري

 

مثال 1: إذا كان $X~N(10,4)$، فأجد كُلاًّ ممّا يأتي:

$1) P\left(X>10\right) 2) P\left(8<X<12\right) 3)P\left(X>12\right)$

 الحل:

بإستعمال القاعدة التجريبية

 $1) P(X>10)$

بما أن الوسط الحسابي للتوزيع 10 والتوزيع توزيع طبيعي ومُنحناه منحنى طبيعي كما في الشكل المجاور 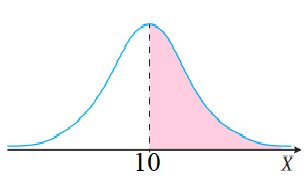 فإنَّ: $P(X>10)=0.5$، لأن المساحة تحت منحنى التوزيع الطبيعي تساوي 1.

 

 

 

 $2) P(8<X<12)$

بما أن(التباين) ${\sigma }^2=4$ فإن الانحراف المعياري يساوي 2، لذلك كلٌّ من القيمة 8 والقيمة 12 تبُعْد إنحرافا معياريا واحدًا عن الوسط الحسابي 10، إذًا:  $P(8<X<12)=P(\mu -\sigma <X<\mu +\sigma )=0.68$

 

 $3) P(X>12)$

بما أن الوسط الحسابي للتوزيع 10 والانحراف المعياري يساوي 2،فإن:

 $$\begin{gathered} 12=10+2 \Rightarrow 12=\mu +\sigma \\ P\left(X>12\right)=P\left(X>\mu +\sigma \right) \end{gathered}$$

كما في الشكل المجاور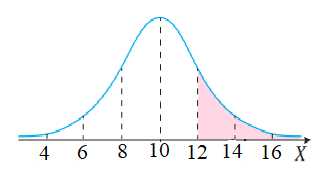 

$$\begin{gathered} P(X>12)=P(X>\mu +\sigma ) \\ =P(X>\mu )-P(\mu <X<\mu +\sigma ) \\ =0.5-0.34=0.16 \end{gathered}$$

 

مثال 2: إذا كان: $X~N(30,9)$، فأجد كُلاًّ ممّا يأتي:

$1) P(X<30) 2) P(27<X<33) 3)P(X>36)$

 الحل:

بإستعمال القاعدة التجريبية

 $1) P(X<30)$

 بما أن الوسط الحسابي للتوزيع 30 والتوزيع توزيع طبيعي،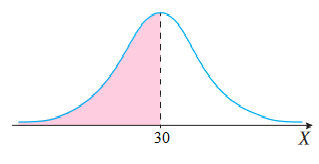 ومُنحناه منحنى طبيعي كما في الشكل 

فإنَّ: $P(X<30)=0.5$، لأن المساحة تحت منحنى التوزيع الطبيعي تساوي 1.

 

 $2) P(27<X<33)$

بما أنْ الوسط الحسابي=30،  والتباين=9 فإن الانحراف المعياري=3 

$\mu =30 و {\sigma }^2=9 \Rightarrow \sigma =3$، وكما هو موضح في الشكل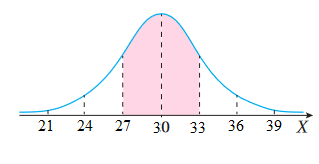

فإنْ:

 

$$\begin{gathered} P(27<X<33)= P(30-3<X<30+3) \\ = P(\mu -\sigma <X<\mu +\sigma ) \\ =68\% \end{gathered}$$

 

 $3) P(X<36)$

بما أن الوسط الحسابي للتوزيع 30 والانحراف المعياري يساوي 3، وكما هو موضح في الشكل فإن: 

$$\begin{gathered} 36=30+6 \Rightarrow 30=\mu +2\sigma \\ P(X<36)=P(X<30)+P(30<X<36) \\ =P(X<\mu )+P(\mu <X<\mu +2\sigma ) \\ =0.5+0.475=0.975 \end{gathered}$$

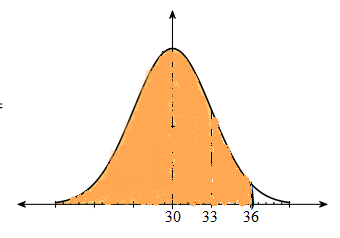
أتحقق من فهمي

 إذا كان: $X~N(60,100)$، فأجد كُلاًّ ممّا يأتي:

$a) P(X<60) b) P(60<X<70) c)P(X>80)$

الإجابة: 

$a) 0.5 b) 0.34 c) 0.025$

 

مثال 3: من الحياة

إذا كان العمر الإفتراضي لمشغل الأقراص المرنة والمنتج من إحدى شركات الكمبيوتر يتبع التوزيع الطبيعي بمتوسط  2000 ساعة، وانحراف معياري 200 ساعة، فإذا تم اختيار وحدة مشغل من هذه الشركة بطريقة عشوائية، فأجد احتمال أن يكون عمرها الإفتراضي:

1) بين 2000 ، 2200 ساعة.

2) بين 1800 ، 2200 ساعة.

3)أقل من 2000 ساعة.

4) أكبر من الوسط وأقل من2400 ساعة.

5) أكبر من 1800 ساعة.

الحل:

 بما أن التوزيع يتبع التوزيع طبيعي فإن $X$ مُتغيِّرًا عشوائيًا طبيعيًا، حيث $X~N(2000,40000)$ 

$\mu =2000 و {\sigma }^2=40000 \Rightarrow \sigma =200$

 $1) P(2000<X<2200)$

$$\begin{gathered} P(2000<X<2200)=P(\mu <X<\mu +\sigma ) \\ =0.34 \end{gathered}$$

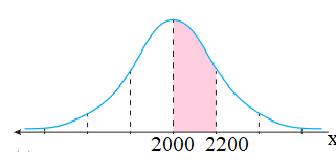
إذًا، احتمال أن يكون عمرها الإفتراضي بين 2000 ، 2200 ساعة هو 0.34

 $2) P(1800<X<2200)$

$$\begin{gathered} P(1800<X<2200)=P(\mu -\sigma <X<\mu +\sigma ) \\ =0.68 \end{gathered}$$

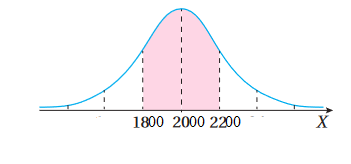
إذًا، احتمال أن يكون عمرها الإفتراضي بين 1800 ، 2200 ساعة هو 0.68.

 $3) P(X<2000)$ 

$$\begin{gathered} P(X<2000)=P(X<\mu ) \\ =0.5 \end{gathered}$$

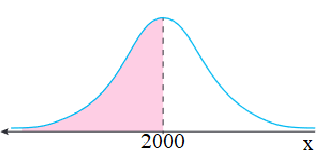
إذًا، احتمال أن يكون عمرها الإفتراضي أقل من 2000 ساعة هو 0.5

 

 $4) P(2000<X<2400)$

$$\begin{gathered} P(2000<X<2400)=P(\mu <X<\mu +2\sigma ) \\ =0.34+0.135 \\ =0.475 \end{gathered}$$

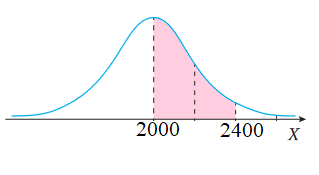
إذًا، احتمال أن يكون عمرها الإفتراضي أكبر من الوسط الحسابي وأقل من2400 ساعة هو 0.475

 

 $5) P(X>1800)$

$$\begin{gathered} P(X>1800)=P(X>\mu -\sigma ) \\ =0.34 + 0.5 \\ =0. 84 \end{gathered}$$

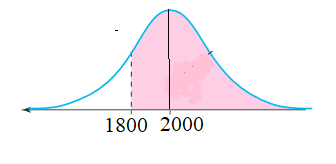
إذًا، احتمال أن يكون عمرها الإفتراضي أكبر من 1800 ساعة هو 0.84

 

أتحقق من فهمي

أعمار: توصلت دراسة إلى أن أعمار الرجال قي إحدى الدول تتبع توزيعًا طبيعيًا، وسطه الحسابي 70 سنة، وانحرافه المعياري 5 سنوات . إذا اختير رجل عشوائيًا، فأجد كُلاً ممّا يأتي:

a) احتمال أنْ يكون عمر الرجل أكثر من 75 سنه. الإجابة: 0.16

b) احتمال أنْ يتراوح عمر الرجل بين 65 و 80 سنه. الإجابة: 0.815