رياضيات فصل ثاني

حُلُولُ أَسْئِلَةٍ أَتَحَقَّقُ مِنْ فَهْمِي 

أنسخُ المضلعَ المرسومَ جانبًا على ورقةِ مربَّعاتٍ، ثمَّ أرسمُ صورتَهُ تحتَ تأثيرِ تكبيرٍ مركزُهُ النقطةُ O ومعامله 3 

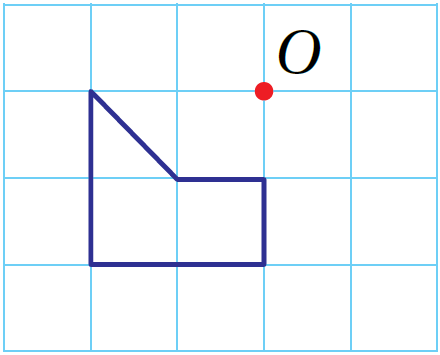
الْخُطْوَةُ 1: أبدأُ بِرسمِ خطوطٍ بِاستعمالِ المسطرةِ ابتداءً مِنْ مركزِ التكبيرِ بِحيثُ يمرُّ كلٌّ منها بأحدِ رؤوسِ المضلع، وَأَمدُّ الخطوطَ على استقامتِها.

الْخُطْوَةُ 2: أقيسُ المسافةَ بينَ مركزِ التكبيرِ وَكلِّ رأسٍ مِنْ رؤوسِ المضلع بِاستعمالِ المسطرةِ، ثمَّ أضربُ القياساتِ الّتي حصلْتُ عليها في 3 

الْخُطْوَةُ 3: أقيسُ المسافاتِ الجديدةَ على الخطوطِ الّتي رسمْتُها في الخطوةِ 1 ابتداءً مِنْ مركزِ التكبيرِ، وَأحدّدُ علامةً لِكلٍّ مِنها.

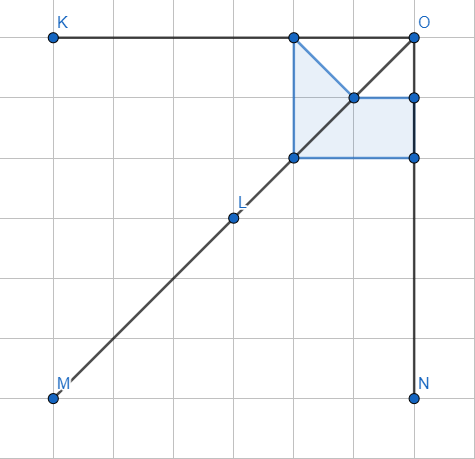
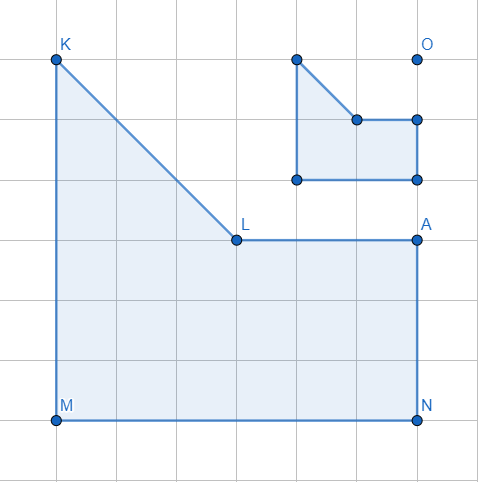
الْخُطْوَةُ 4: أَصِلُ بينَ نقاط المضلع الجديد

 

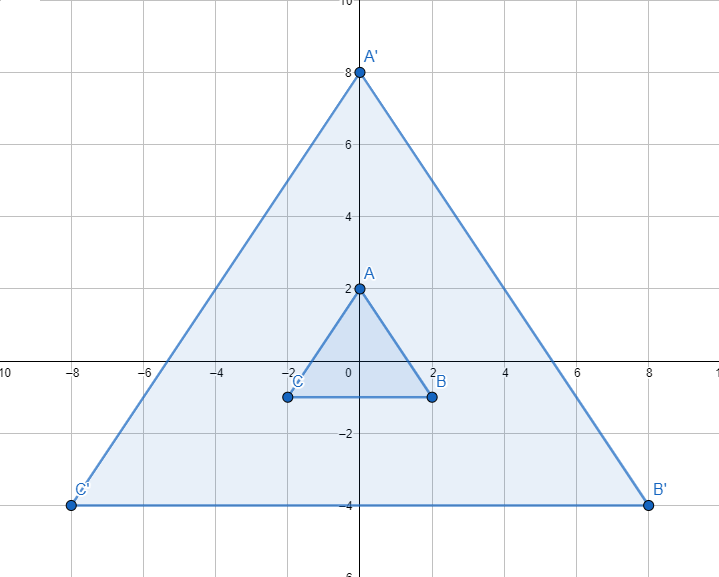
2)أرسمُ ΔABC الّذي إحداثياتُ رؤوسِهِ $\mathbf{A}\mathbf{(}\mathbf{0}\mathbf{,}\mathbf{ }\mathbf{2}\mathbf{)}\mathbf{,}\mathbf{ }\mathbf{B}\mathbf{(}\mathbf{2}\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{1}\mathbf{)}\mathbf{,}\mathbf{ }\mathbf{C}\mathbf{(}\mathbf{-}\mathbf{2}\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{1}\mathbf{)}$في المستوى الإحداثيِّ، ثمَّ أرسمُ صورتَهُ تحتَ تأثيرِ تكبيرٍ مركزُهُ نقطةُ الأصلِ وَمُعامِلُهُ 4 

الْخُطْوَةُ 1: أرسمُ المثلث ABC في المستوى الإحداثيِّ

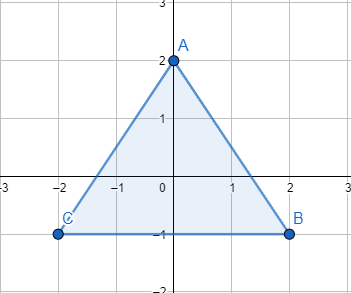
الْخُطْوَةُ 2:أَجِدُ إحداثياتِ رؤوسِ الصورةِ بِضربِ الإحداثيِّ x وَالإحداثيِّ y لِكلِّ رأسٍ مِنْ رؤوسِ الشكلِ الأصليِّ في 4

إحداثياتُ الصورةِ		إحداثياتُ رؤوسِ الشكلِ الأصليِّ
(4x, 4y)	$\underset{}{\overset{}{\to }}$	(x, y)
A'(0, 8)	$\underset{}{\overset{}{\to }}$	A(0, 2)
B'(8, -4)	$\underset{}{\overset{}{\to }}$	B(2, -1)
C'(-8, -4)	$\underset{}{\overset{}{\to }}$	C(-2, -1)

الْخُطْوَةُ 3: أرسمُ المضلعَ 'A'B'C في المستوى الإحداثيِّ.

 

يبيّنُ الشكلُ المجاورُ  ΔUOV وَصورتَهُ ΔXOY الناتجةَ عَنْ تكبيرٍ  مركزُهُ نقطةُ الأصلِ، أَجِد:

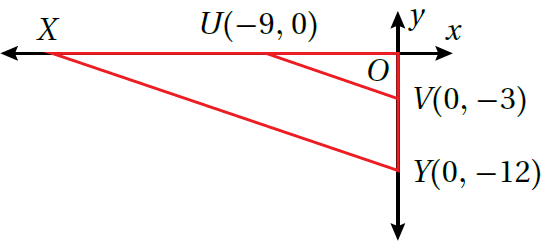
3)معاملَ التكبيرِ. 

 بما أن ΔUOV~ ΔXOY فَإنَّ النسبةَ بينَ طولَيْ أيِّ ضلعَينِ متناظرَينِ تساوي معاملَ التكبيرِ $\frac{\mathrm{YO}}{\mathrm{VO}}=\frac{-12}{-3}=4$ 

معامل التكبير = 4 

4) إحداثيَّيِ الرأسِ X

المناظرِ لَهُ في معاملِ التكبير U عَنْ ضربِ إحداثيَّيِ الرأسِ X ينتجُ إحداثيّا الرأسِ

$(-9, 0)\to (-9\times 4, 0\times 4)\to (-36, 0)$

اذن X= -36,0

 

تُظهرُ العدسةُ المكبِّرةُ المجاورةُ الأجسامَ أكبرَ بِ 7 مراتٍ مِنْ حجمِها الأصليِّ. إذا كانَ طولُ بذرةِ التفاحِ المجاورةِ تحتَ العدسةِ 1.75cm فَأَجِدُ الطولَ الحقيقيَّ لِبذرةِ التفاحِ. 

1.75 = 7 × K          الطولُ الحقيقيُّ × طولُ الصورةِ = معاملُ التكبيرِ

0.25 = K              أقسمُ طرفَِ المعادلةِ على 7

اذن الطولَ الحقيقيَّ لِبذرةِ التفاحِ = 0.25cm

---

---

حُلُولُ أَسْئِلَةٍ أَتَدرب وأحل المسائل 

أنسخُ كلَّ مضلعٍ مِمّا يأتي على ورقة مربَّعاتٍ، ثمَّ أرسمُ صورتَهُ تحتَ تأثيرِ تكبيرٍ مركزُهُ النقطةُ O مستعمِلًا معاملَ التكبيرِ المعطى أسفَلَهُ: 

1)

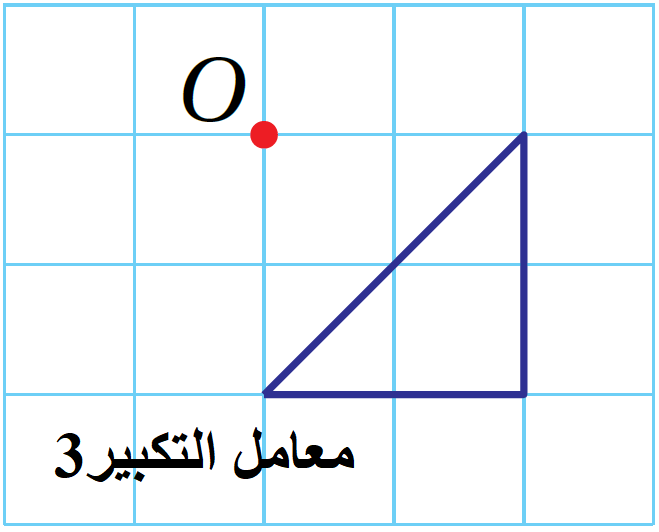
الْخُطْوَةُ 1: أبدأُ بِرسمِ خطوطٍ بِاستعمالِ المسطرةِ ابتداءً مِنْ مركزِ التكبيرِ بِحيثُ يمرُّ كلٌّ منها بأحدِ رؤوسِ المضلع، وَأَمدُّ الخطوطَ على استقامتِها.

الْخُطْوَةُ 2: أقيسُ المسافةَ بينَ مركزِ التكبيرِ وَكلِّ رأسٍ مِنْ رؤوسِ المضلع بِاستعمالِ المسطرةِ، ثمَّ أضربُ القياساتِ الّتي حصلْتُ عليها في 3 (معامل التكبير)

الْخُطْوَةُ 3: أقيسُ المسافاتِ الجديدةَ على الخطوطِ الّتي رسمْتُها في الخطوةِ 1 ابتداءً مِنْ مركزِ التكبيرِ، وَأحدّدُ علامةً لِكلٍّ مِنها.

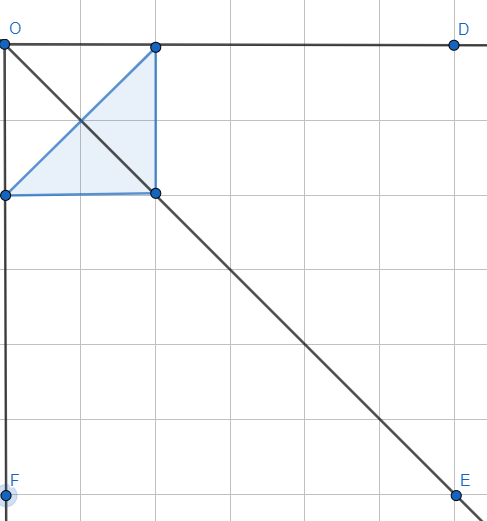
الْخُطْوَةُ 4: أَصِلُ بينَ نقاط المثلث الجديد

 

 

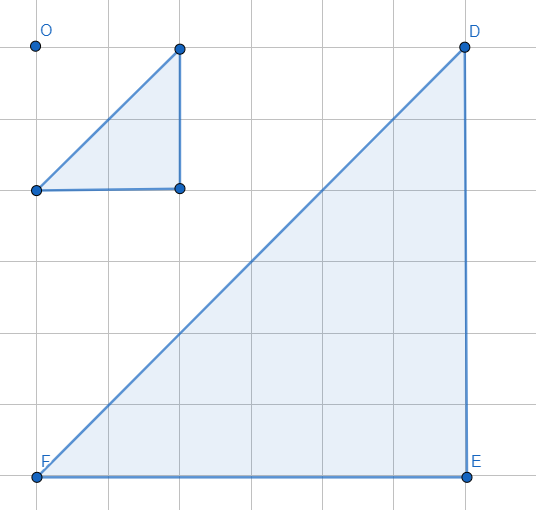
2) 

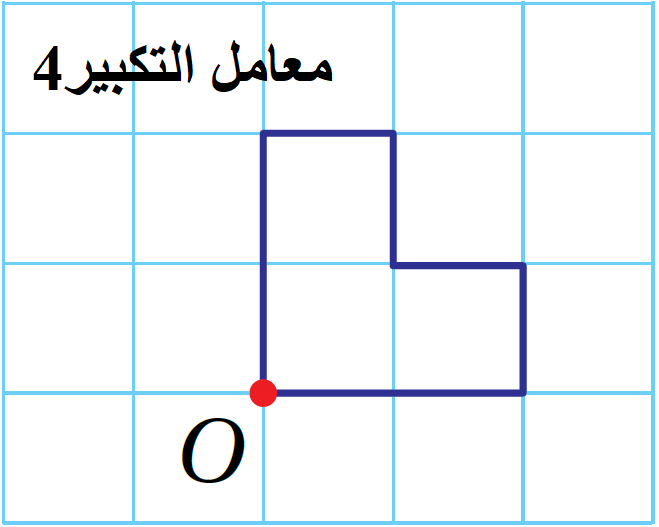
الْخُطْوَةُ 1: أبدأُ بِرسمِ خطوطٍ بِاستعمالِ المسطرةِ ابتداءً مِنْ مركزِ التكبيرِ بِحيثُ يمرُّ كلٌّ منها بأحدِ رؤوسِ المضلع، وَأَمدُّ الخطوطَ على استقامتِها.

الْخُطْوَةُ 2: أقيسُ المسافةَ بينَ مركزِ التكبيرِ وَكلِّ رأسٍ مِنْ رؤوسِ المضلع بِاستعمالِ المسطرةِ، ثمَّ أضربُ القياساتِ الّتي حصلْتُ عليها في 4  (معامل التكبير)

الْخُطْوَةُ 3: أقيسُ المسافاتِ الجديدةَ على الخطوطِ الّتي رسمْتُها في الخطوةِ 1 ابتداءً مِنْ مركزِ التكبيرِ، وَأحدّدُ علامةً لِكلٍّ مِنها.

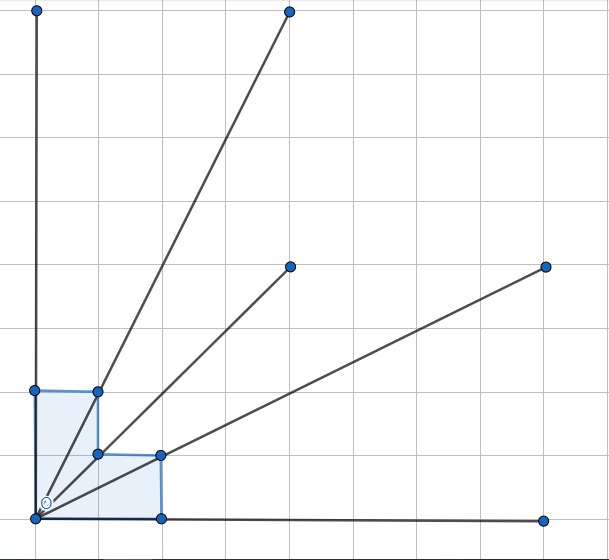
الْخُطْوَةُ 4: أَصِلُ بينَ نقاط المضلع الجديد

 

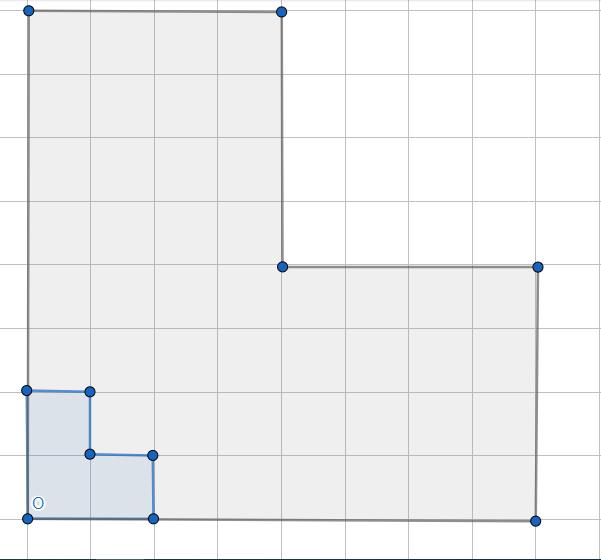
أَجِدُ معاملَ التكبيرِ في كلٍّ ممّا يأتي:

3)

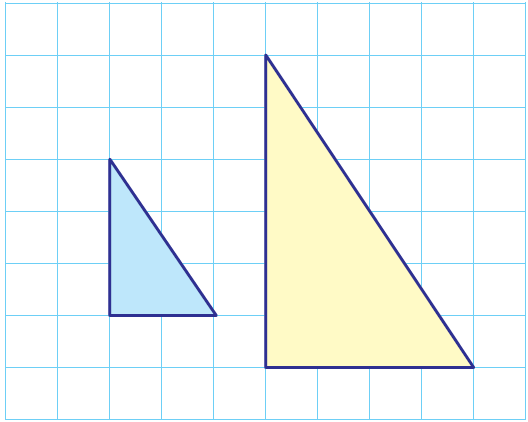
معاملَ التكبيرِ 2

4)

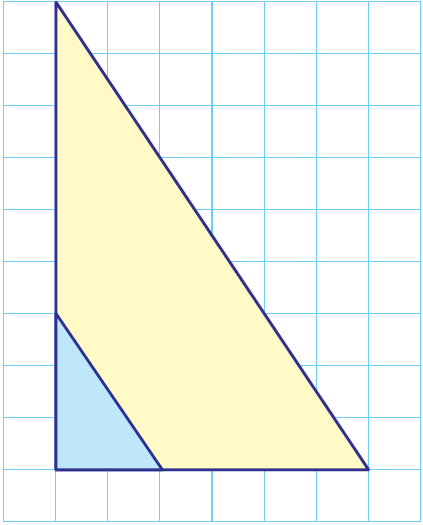
معاملَ التكبيرِ 3

5)

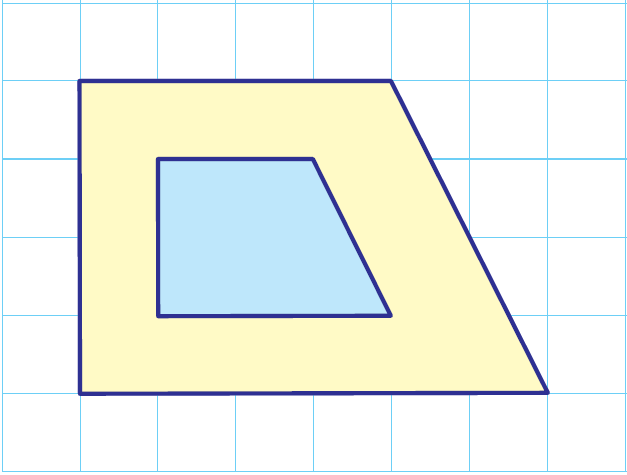
معاملَ التكبيرِ 2
 

أنسخُ كلَّ مضلعٍ مِمّا يأتي على ورقةِ مربَّعاتٍ، ثم أرسمُ صورةً لَهُ تحتَ تأثيرِ تكبيرٍ مركزُهُ نقطةُ الأصلِ، مستعمِلًا معاملَ التكبيرِ المعطى أسفلَهُ:

6)

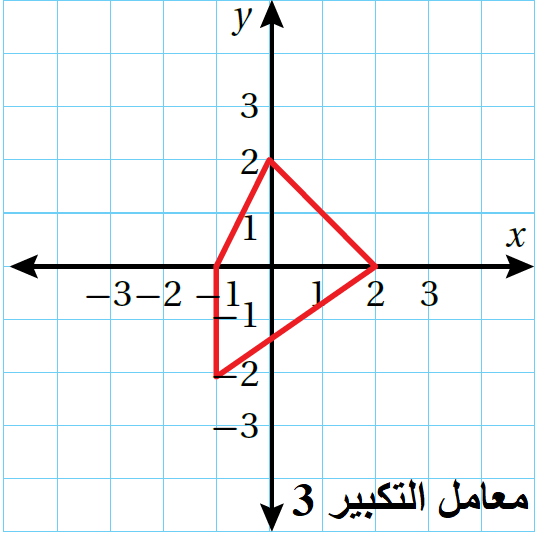
الْخُطْوَةُ 1: أَجِدُ إحداثياتِ رؤوسِ الصورةِ بِضربِ الإحداثيِّ x وَالإحداثيِّ y لِكلِّ رأسٍ مِنْ رؤوسِ الشكلِ الأصليِّ في 3

إحداثياتُ الصورةِ		إحداثياتُ رؤوسِ الشكلِ الأصليِّ
(3x, 3y)	$\underset{}{\overset{}{\to }}$	(x, y)
A'(6, 0)	$\underset{}{\overset{}{\to }}$	A(2, 0)
B'(0, 6)	$\underset{}{\overset{}{\to }}$	B(0, 2)
C'(-3, 0)	$\underset{}{\overset{}{\to }}$	C(-1, 0)
D'(-3, -6)	$\underset{}{\overset{}{\to }}$	D(-1, -2)

الْخُطْوَةُ 2: أرسمُ المضلعَ  في المستوى الإحداثيِّ.

 

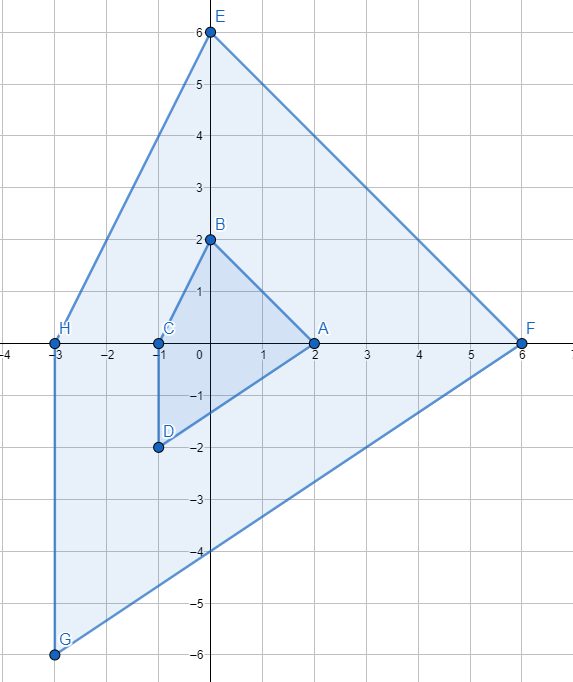
7)

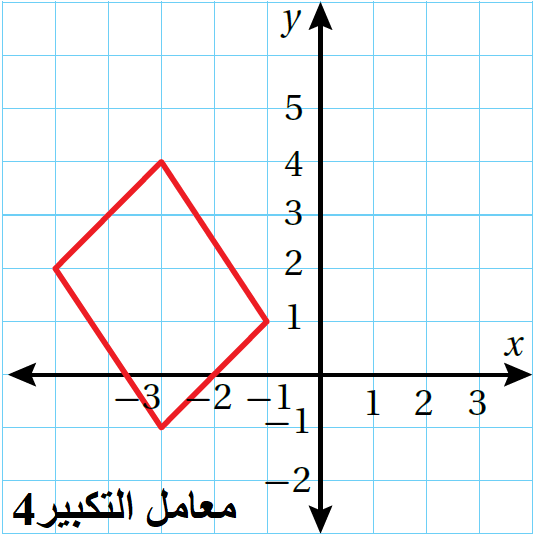
الْخُطْوَةُ 1: أَجِدُ إحداثياتِ رؤوسِ الصورةِ بِضربِ الإحداثيِّ x وَالإحداثيِّ y لِكلِّ رأسٍ مِنْ رؤوسِ الشكلِ الأصليِّ في 4

إحداثياتُ الصورةِ		إحداثياتُ رؤوسِ الشكلِ الأصليِّ
(4x, 4y)	$\underset{}{\overset{}{\to }}$	(x, y)
A'(-4, 4)	$\underset{}{\overset{}{\to }}$	A(-1, 1)
B'(-12, 16)	$\underset{}{\overset{}{\to }}$	B(-3, 4)
C'(-20, 8)	$\underset{}{\overset{}{\to }}$	C(-5, 2)
D'(-12, -4)	$\underset{}{\overset{}{\to }}$	D(-3, -1)

الْخُطْوَةُ 2: أرسمُ المضلعَ  في المستوى الإحداثيِّ.

 

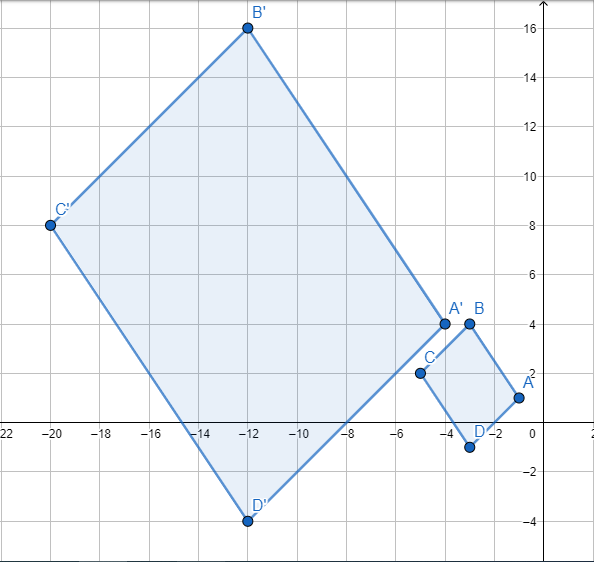
يبيّنُ الشكلُ المجاورُ المثلثَ ΔOKL وَصورتَهُ ΔOMN الناتجةَ عَنْ تكبيرٍ مركزُهُ نقطةُ الأصلِ، أَجِدُ:

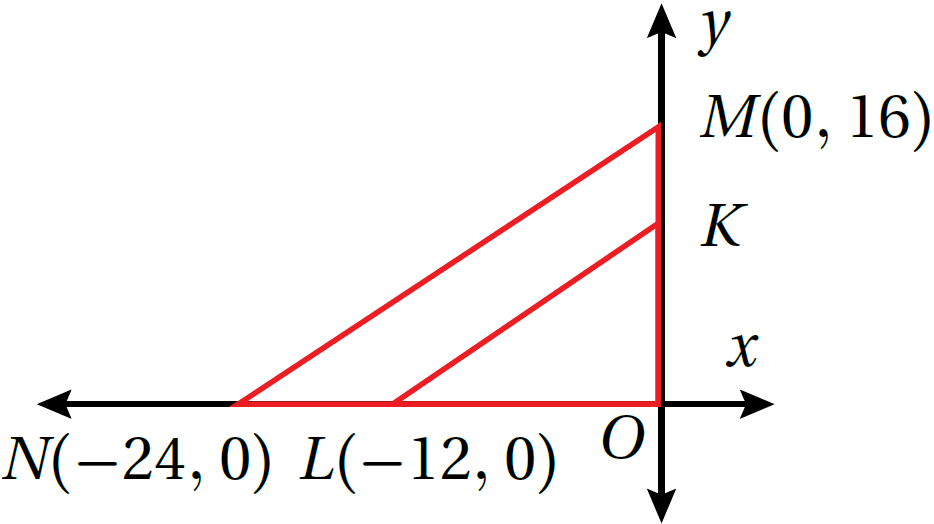
8) معاملَ التكبيرِ.

من الاضلاع المتناسبة نجد معامل التكبير $\frac{NO}{LO}=\frac{-24}{-12}=2$

اذن معامل التكبير = 2

9) إحداثيَّيِ الرأسِ K

نجد احداثي الراس K باستخدام معامل التكبير 

$$\begin{gathered} \frac{MO}{KO}=\frac{16}{K}=2 \\ K=8 \end{gathered}$$

احداثيات الراس (K=(0,8

 

10)عدساتٌ: تُظهرُ العدسةُ المكبِّرةُ المجاورةُ الأجسامَ أكبرَ بمرّتَينِ مِنْ حجمِها الأصليِّ. إذا كانَ طولُ بصمةِ الإبهامِ المجاورةِ تحتَ العدسةِ 2.5cm أَجِدُ طولَ البصمةِ الحقيقيَّ.

2.5 = 2 × C          الطولُ الحقيقيُّ × طولُ الصورةِ = معاملُ التكبيرِ

1.25 =C              أقسمُ طرفَِ المعادلةِ على 2

اذن طولَ البصمةِ الحقيقيَّ= 1.25cm

11) تصميمٌ جرافيكيٌّ: أنشأَ مصمّمٌ الشعارَ المجاورَ لِشركةِ عقاراتٍ، وَلكنّهُ يحتاجُ إلى جعلِهِ أكبرَ مرتَينِ لِاستخدامِهِ على لافتةٍ. أرسمُ الشعارَ تحتَ تأثيرِ تكبيرٍ . مركزُهُ نقطةُ الأصلِ وَمعاملُهُ 2

 

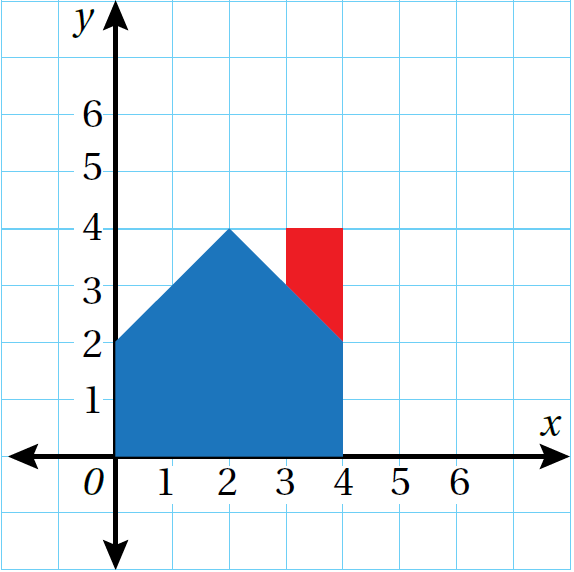
الْخُطْوَةُ 1: أَجِدُ إحداثياتِ رؤوسِ الصورةِ بِضربِ الإحداثيِّ x وَالإحداثيِّ y لِكلِّ رأسٍ مِنْ رؤوسِ الشكلِ الأصليِّ في 2

إحداثياتُ الصورةِ		إحداثياتُ رؤوسِ الشكلِ الأصليِّ
(2x, 2y)	$\underset{}{\overset{}{\to }}$	(x, y)
A'(0, 0)	$\underset{}{\overset{}{\to }}$	A(0, 0)
B'(8,0)	$\underset{}{\overset{}{\to }}$	B(4, 0)
C'(8,4)	$\underset{}{\overset{}{\to }}$	C(4, 2)
D'(4,8)	$\underset{}{\overset{}{\to }}$	D(2, 4)
E'(0,4)	$\underset{}{\overset{}{\to }}$	E(0,2)
F'(6,6)	$\underset{}{\overset{}{\to }}$	F(3,3)
J'(6,8)	$\underset{}{\overset{}{\to }}$	J(3,4)
H'(8,8)	$\underset{}{\overset{}{\to }}$	H(4,4)
I'(8,4)	$\underset{}{\overset{}{\to }}$	I(4,2)

الْخُطْوَةُ 2: أرسمُ الشعار في المستوى الإحداثيِّ.

 

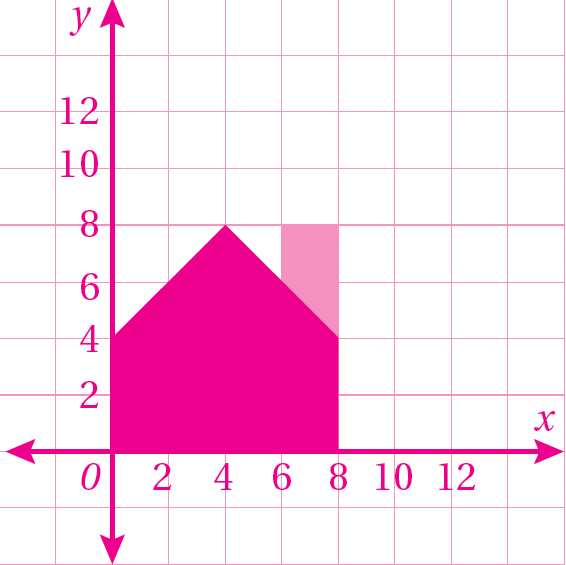
تبريرٌ: مثلثٌ إحداثياتُ رؤوسِهِ (1,A(1, 2), B(1, 0), C(3 كُبِّرَ بِاستعمالِ نقطةِ الأصلِ كَمركزٍ لِلتكبيرِ. إذا كانَ إحداثيّا أحدِ رؤوسِ الصورةِ (18,6) أَجِدُ كلاً مِمّا يلي :

12) معاملَ التكبيرِ 

6 ، لأن النقطة الوحيدة التي ضرب إحداثياها بنفس العدد هي (1,C(3 فعند ضرب إحداثياها بالعدد 6 أحصل على النقطة (18,6)

13) إحداثياتِ الرؤوسِ الأُخرى.

A'(6, 12), B'(6, 0)

 

14) أكتشفُ الخطأَ: رسمَ عدنانُ مستطيلً طولُهُ 3cm وعرضه 2cm  ثمَّ أوجدَ صورةً لَهُ تحتَ تأثيرِ معاملِ تكبيرٍ قيمتُهُ 5، فَكانَ عَرضُ المستطيلِ الجديدِ 15cm أبيّنُ الخطأَ الّذي وقعَ فيهِ عدنانُ، وَأُصححُهُ.

15cm هو طول المستطيل الجديد وليس عرضه.

 

15) تحدٍّ: يُظهرُ الشكلُ المجاورُ صورةً لِاحدى دُمى الماتريوشكا. أرسمُ صورةً لِلدّميةِ تحتَ تأثيرِ تكبيرٍ معاملُهُ 2 وَمركزُهُ نقطةُ الأصلِ

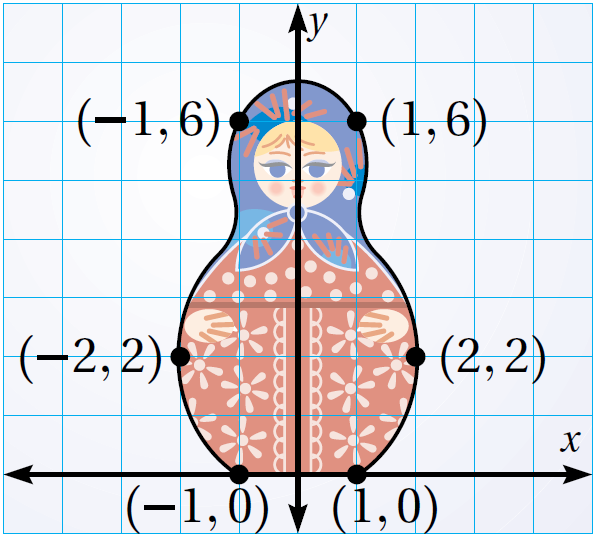
الْخُطْوَةُ 1: أَجِدُ إحداثياتِ رؤوسِ الصورةِ بِضربِ الإحداثيِّ x وَالإحداثيِّ y لِكلِّ رأسٍ مِنْ رؤوسِ الشكلِ الأصليِّ في 2

إحداثياتُ الصورةِ		إحداثياتُ رؤوسِ الشكلِ الأصليِّ
(2x, 2y)	$\underset{}{\overset{}{\to }}$	(x, y)
A'(2,0)	$\underset{}{\overset{}{\to }}$	A(1,0)
B'(4,4)	$\underset{}{\overset{}{\to }}$	B(2,2)
C'(2,12)	$\underset{}{\overset{}{\to }}$	C(1, 6)
D'(-2,12)	$\underset{}{\overset{}{\to }}$	D(-1, 6)
E'(-4,4)	$\underset{}{\overset{}{\to }}$	E(-2,2)
F'(-2,0)	$\underset{}{\overset{}{\to }}$	F(-1,0)

الْخُطْوَةُ 2: أرسمُ الدمية في المستوى الإحداثيِّ.

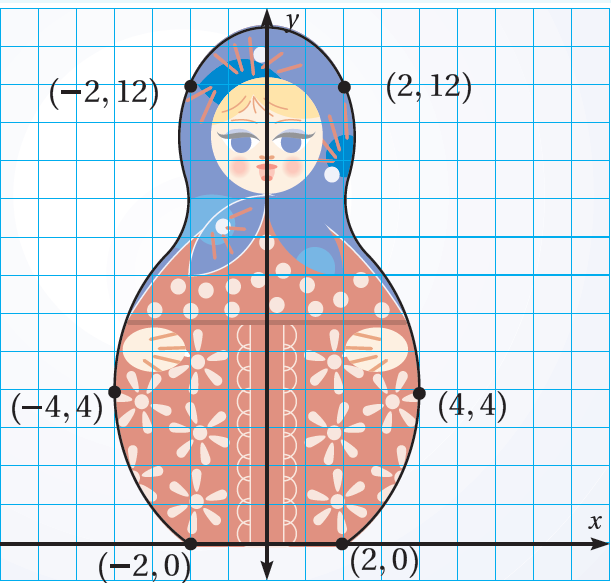
16) أكتبُُ كيفَ أَجِدُ معاملَ التكبيرِ لِشكلٍ مرسومٍ في المستوى الإحداثيِّ؟ 

عن طريق إيجاد النسب بين الاضلاع المتناظرة وذلك بقسمة المسافة بين نقطتين على صورة الشكل على المسافة بين النقطتين المناظرتين لها في الشكل الأصلي .

---

---

حلول أسئلة كتاب التمارين 

أنسخُ كلَّ مضلَّعٍ مِمّا يأتي على ورقِ مربَّعاتٍ، ثمَّ أرسمُ صورةً لَهُ تحتَ تأثيرِ تكبيرٍ مركزُهُ النقطةُ A مستعمِلً قيمةَ معاملِ التكبيرِ المُعطاةَ أسفَلَهُ:

1)

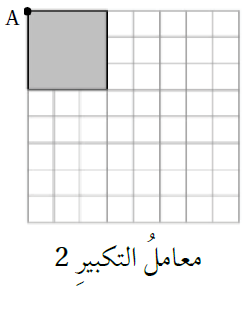
الحل:

 

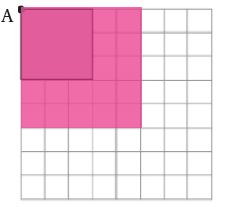
2) 

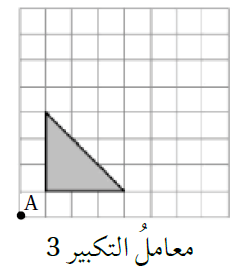
الحل:

 

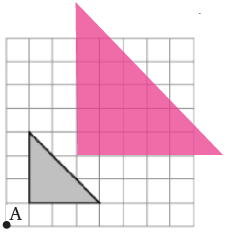
: أنسخُ كلَّ مضلَّعٍ مِمّا يأتي على ورقِ مربَّعاتٍ، ثمَّ أرسمُ صورةً له تحتَ تأثيرِ تكبيرٍ مركزُهُ نقطةُ الأصلِ، وَمعاملُهُ 2

3)

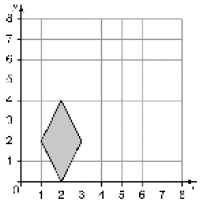
الحل:

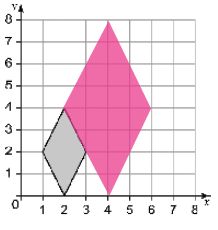
4)

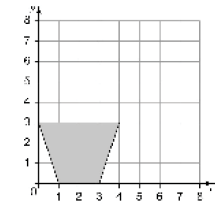
الحل:

 

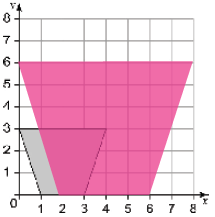
5) أرسمُ ΔABC الّذي إحداثياتُ رؤوسِهِ A(2, 2), B(6, 2), C(6,4) في المستوى الإحداثيِّ، ثمَّ أرسمُ صورتَهُ تحتَ تأثيرِ تكبيرٍ مركزُهُ نقطةُ الأصلِ وَمُعامِلُهُ 4

 

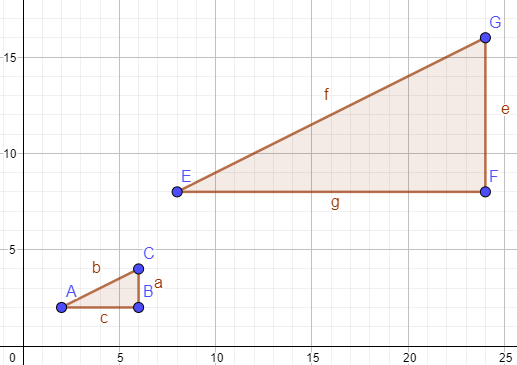
.A ليسَ تكبيرًا لِلمضلَّعِ B في السؤالَينِ 6 وَ 7 أفسّرُ سببَ أَنَّ المضلَّعَ

6)

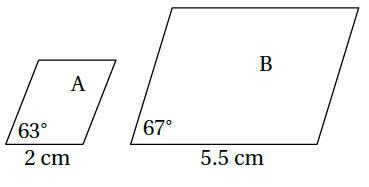
عدم تطابق الزوايا المتناظرة

7)

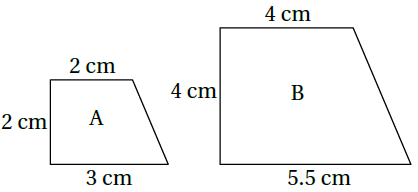
عدم تناسب الأضلاع المتناظرة

$\frac{5.5}{3}\ne \frac{4}{2}$