رياضيات فصل أول

الاقترانُ التربيعيُّ

الاقتران التربيعي : اقتران يمكن كتابته على الصورة $f\left(x\right)=a{x}^2+bx+c$ ، والتي تُسمى الصورة القياسيّة للاقتران التربيعيّ، وَمن أمثلتهِ: 

$f\left(x\right)=5x^2-2x+1 h\left(x\right)=x^2+4x g\left(x\right)=8x^2$

•• يُعَدُّ الاقترانُ  $f\left(x\right)=x^2$ أبسطَ صورِ الاقترانِ التربيعيِّ ؛ لِذا يُسَمّى الاقترانَ الرئيسَ لعائلةِ الاقتراناتِ التربيعيَّةِ.

يأخذُ التمثيلُ البيانيُّ للاقترانِ التربيعيِّ شكلَ الحرفِ الإنجليزيِّ U ، وَيُسَمّى قطعًا مُكافِئًا ، كما في الشكلِ المُجاورِ ، الذي يُظهِرُ التمثيلَ البيانيَّ  للاقترانِ $f\left(x\right)=x^2$

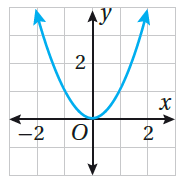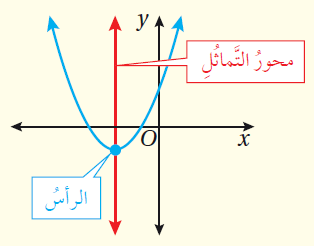
محورُ التَّماثُلِ :  هُوَ المُستقيمُ الرأسيُّ الذي يقسِمُ القطعَ المُكافِئَ إلى جُزأيْنِ مُتطابقَيْنِ، ويقطعُهُ في نقطةٍ واحدةٍ تُسَمّى الرأسَ 

مفهومٌ أساسيٌّ (محورُ تَماثُلِ الاقترانِ التربيعيِّ ورأسُهُ) 

مُعادلةُ محورِ التَّماثُلِ لمُنحنى الاقترانِ التربيعيِّ $f\left(x\right)=a{x}^2+bx+c$ ؛ حيثُ a ≠ 0 هي : $x=-\frac{b}{2a}$ وإحداثِيّا رأسِهِ هما : $\left(-\frac{b}{2a}, f(-\frac{b}{2a})\right)$

••• مجال الاقتران التربيعي ومداه 

يكونُ التمثيلُ البيانيُّ للاقترانِ التربيعيِّ $f\left(x\right) = a{x}^2+ bx + c$  ؛ حيثُ a ≠ 0 ، مفتوحًا للأعلى إذا كان a > 0 ، وَتُسَمّى أدنى نقطة فيه نقطة القيمة الصُّغرى ، ويكون مفتوحًا للأسفل إذا كان a < 0 ، وتُسمى أعلى نقطة فيه نقطة القيمة العُظمى ، وتُمثل نقطة القيمة الصُّغرى أو نقطة القيمة العُظمى رأس القطع  المُكافئ.

---

مجال الاقتران التربيعيِّ هُو جميع الأعداد الحقيقية ، أمّا مَداهُ فيمكن تحديدُهُ كالآتي :

مفهوم أساسيّ (مَدى الاقتران التربيعيّ) 

إذا كان $f\left(x\right)=a{x}^2+bx+c$  ؛ حيثُ a ≠ 0 ، فإنَّ مَدى (f(x يكونُ :

• مجموعة الأعداد الحقيقية التي تزيد على القيمة الصُّغرى أو تُساويها إذا كان a > 0  

• مجموعة الأعداد الحقيقية التي تقلّ عن القيمة العُظمى أو تُساويها إذا كان a < 0

مفهومٌ أساسيٌّ (تمثيلُ الاقترانِ التربيعيِّ بيانيًّا)

لتمثيل الاقتران التربيعيّ بيانيًّا، أتَّبِع الخُطوات الآتية:

الخطوةُ 1 : أُحَدِّدُ اتِّجاهَ فتحةِ القطع المُكافئِ، وَأَجِدُ مُعادلة محور التماثل وإحداثِيَّيِ الرأس، وَأُحَدِّدُ إذا كان يُمثل نقطة صُغرى أمْ نقطة عُظمى.

الخطوةُ 2 : أَجِدُ نقطةَ تقاطع الاقتران مع المحور y.

الخطوةُ 3 : أَجِدُ نقطةً أُخرى باختيارِ قيمةٍ لِـ x تقع في الجانب الذي يقعُ فيهِ المقطع y يمين محور التَّماثل أو يساره.

الخطوةُ 4 : أُمَثّل رأس القطع والنقطتين اللتين أوجدتهما من الخطوتين 2 و 3، ثمّ أستعمل التماثل لأعكس النقطتين من الخُطوتين 2 و 3 حول محور التَّماثُلِ؛ لإيجاد نقطتين أُخرَيَيْنِ على التمثيل البيانيّ.

الخطوةُ 5: أصل بين النقاطِ بِمُنحنًى أملَسَ.