الاحتمالُ الهندسيُّ

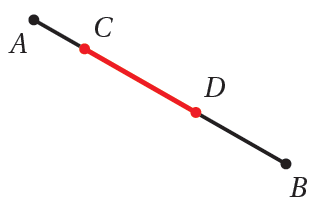
يُبيِّنُ الشكلُ المجاورُ القطعةَ المستقيمةَ AB التي تحوي القطعةَ المستقيمةَ CD .

إذا اختيرَتْ عشوائيًّا نقطةٌ منَ النقاطِ الواقعةِ على AB ، ولتكنْ K، فإنَّ احتمالَ وقوعِ

K على CD يساوي نسبةَ طولِ CD إلى طولِ AB ؛ لأنَّ جميعَ النقاطِ الواقعةِ على AB تُمثِّلُ

عناصرَ الفضاءِ العينيِّ للتجربةِ العشوائيةِ، وجميعَ النقاطِ الواقعةِ على CD تُمثِّلُ عناصرَ

الحادثِ.

$P(\overline{CD} \mathrm{على} K \mathrm{وقوع}) = \frac{CD}{AB}$

••أتعلَّمُ : يتساوى الاحتمالُ في تجربةِ اختيارِ النقطةِ K ؛ لأنَّ فرصةَ الوقوعِ

هيَ نفسُها لأيِّ نقطةٍ تقعُ على $\overline{AB}$

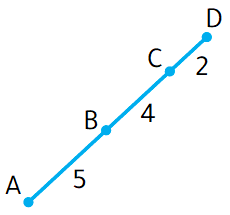
مُعتمِدًا الشكلَ المجاور ، إذا اختيرَت عشوائيًّا نقطة تقع على $\overline{AD}$ ، فأجدُ كُلًّ ممّا يأتي : 

1) احتمالُ وقوعِ النقطةِ على $\overline{BC}$

2) احتمالُ وقوعِ النقطةِ على $\overline{AB}$

3) احتمالُ عدم وقوعِ النقطةِ على $\overline{CD}$

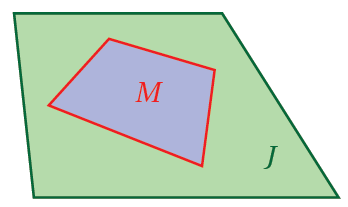
يُبيِّنُ الشكلُ المجاورُ المنطقةَ J التي تحوي المنطقةَ M.

إذا اختيرَتْ عشوائيًّا نقطةٌ منَ النقاطِ الواقعةِ في المنطقةِ J ، ولتكنْ K، فإنَّ احتمالَ

وقوعِ K في المنطقةِ M يساوي نسبةَ مساحةِ المنطقةِ M إلى مساحةِ المنطقةِ J ؛ لأنَّ

جميعَ النقاطِ في المنطقةِ J تُمثِّلُ عناصرَ الفضاءِ العينيِّ للتجربةِ، وجميعَ النقاطِ في

المنطقةِ M تُمثِّلُ عناصرَ الحادثِ.

$P(M \mathrm{المنطقة} \mathrm{في} K \mathrm{وقوع}) = \frac{(M \mathrm{المنطقة} \mathrm{مساحة})}{(J \mathrm{المنطقة} \mathrm{مساحة})}$

•• أتعلَّم : يتساوى الاحتمالُ في تجربةِ اختيارِ النقطةِ  K ؛ لأنَّ فرصةَ الوقوعِ هيَ نفسُها لأيِّ

   نقطةٍ تقعُ في المنطقةِ

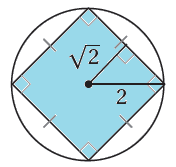
مثال 2 : 

إذا اختيرَتْ نقطةٌ عشوائيًّا من الشكل المجاور، فأجدُ احتمالَ وقوعِها في

المنطقةِ المُظلَّلةِ باللونِ الأزرقِ:

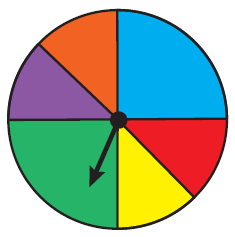
إذا دُوِّرَ المُؤشِّرُ في القرصِ المجاورِ عشوائيًّا، فإنَّ احتمالَ توقُّفِ المُؤشِّرِ عندَ القطاعِ الأخضرِ

يساوي نسبةَ قياسِ زاويةِ القطاعِ الأخضرِ إلى مجموعِ الزوايا حولَ مركزِ الدائرةِ؛ لأنَّ جميعَ

المواقعِ في الدائرةِ تُمثِّلُ عناصرَ الفضاءِ العينيِّ للتجربةِ، وجميعَ المواقعِ في القطاعِ الأخضرِ

تُمثِّلُ عناصرَ الحادثِ.

$P(\mathrm{الأخضر} \mathrm{القطاع} \mathrm{عند} \mathrm{المؤشر} \mathrm{توقف}) =\frac{(\mathrm{الأخضر} \mathrm{القطاع} \mathrm{زاوية})}{(\mathrm{الدائرة} \mathrm{مركز} \mathrm{حول} \mathrm{الزوايا} \mathrm{مجموع})}$

•• أتعلَّمُ : يتساوى الاحتمالُ في تجربةِ توقُّفِ المُؤشِّرِ عندَ أيِّ موقعٍ في الدائرةِ؛ لأنَّ فرصةَ

   الوقوعِ هيَ نفسُها لأيِّ موقعٍ يتوقَّفُ عندَهُ المُؤشِّرُ.

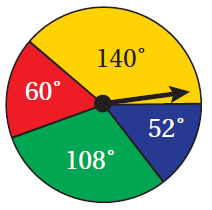
مُعتمِدًا زوايا القطاعاتِ الظاهرةَ على القرصِ المجاورِ، أجدُ كُلًّ ممّا يأتي بعدَ تدويرِ مُؤشِّرِ القرصِ :
1) احتمالُ توقُّفِ مُؤشِّرِ القرصِ عندَ القطاعِ الأحمر.

2) احتمالُ توقُّفِ مُؤشِّرِ القرصِ عندَ القطاعِ الأزرقِ أوِ القطاعِ الأخضر.