رياضيات أدبي فصل أول

احتمال المتغير العشوائي

Probability of a Random Variable

فكرة الدرس : إيجاد احتمالات قِيَم متغير عشوائي في تجربة عشوائية.

التوزيع الاحتمالي للتجربة العشوائية هو اقتران يربط قِيَم المتغير العشوائي باحتمالات وقوعها في التجربة، ويُرمَز إلى اقتران التوزيع الاحتمالي
بالرمز P(X) ، وقد يُكتَب في صورة (P(X = x.

• مجال التوزيع الاحتمالي هو مجموعة قِيَم المتغير العشوائي، ومداه مجموعة قِيَم الاحتمالات المقابلة. 
• يُمكِن التعبير عن اقتران التوزيع الاحتمالي بصورة جدول، أو تمثيل بياني.

مثال : 

في تجربة إلقاء ثلاث قطع نقد متمايزة عشوائيًّا، إذا دلَّ المتغير العشوائي X على عدد مرّات ظهور الصورة، فأجد كل مما يأتي :

a) التوزيع الاحتمالي في صورة جدول.
b) التوزيع الاحتمالي في صورة تمثيل بياني.

الحل :

• فضاء العيِّنة لهذه التجربة هو : $\Omega =\{ =(H,H,H) , (H,H,T) , (H,T,H) , (H,T,T) , (T,T,H) , (T,H,T) , (T,H,H) , (T,T,T\left)\right\}$

• القيم التي يأخذها المتغير العشوائي X هي : 0 ، 1 ، 2 ، 3  

• أجد احتمال كل قيمة للمتغير العشوائي X ، وبذلك تكون قِيَم اقتران التوزيع الاحتمالي للمتغير العشوائي X هي : 

           $P (x = 0) = \frac{1}{8} , P (x =1) = \frac{3}{8} , P (x = 2) = \frac{3}{8} , P (x = 3) = \frac{1}{8}$

a) التوزيع الاحتمالي في صورة جدول.

أنشئ جدولاً على النحو الآتي : 

x	0	1	2	3
P(x)	$\frac{1}{8}$	$\frac{3}{8}$	$\frac{3}{8}$	$\frac{1}{8}$

 

   

 

 

b) التوزيع الاحتمالي في صورة تمثيل بياني

أضع قِيَم المتغير العشوائي على المحور الأفقي، وقِيَم الاحتمال المقابلة لها على المحور الرأسي، ثم أرسم الأعمدة البيانية كما في الشكل المجاور.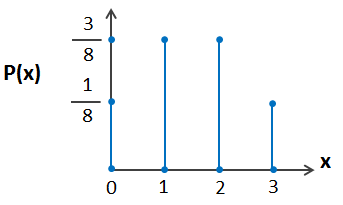

 

 

 

 

 

ألاحظ أنّ :  $\frac{1}{8}+\frac{3}{8}+\frac{3}{8}+\frac{1}{8}=1$  ، أي أنّ مجموع قِيَم اقتران التوزيع الاحتمالي P(x) هو  1 

 

---

 

مفهوم أساسي (اقتران التوزيع الاحتمالي)

بالكلمات : إذا كان X متغيرًا عشوائيًّا ، فإنَّ مجموع قِيَم اقتران التوزيع الاحتمالي P(x) هو 1

بالرموز : إذا كان X متغيرًا عشوائيًّا ، فإنَّ : $\sum _{}P\left(x\right) = 1$

 

• إنَّ معرفة مجموع احتمالات قِيَم المتغير العشوائي في تجربة عشوائية تساعد على إيجاد احتمالات مجهولة، واحتمالات ضمن شروط مُحدَّدة على قِيَم المتغير العشوائي.

 مثال :

في تجربة عشوائية ، كان التوزيع الاحتمالي للمتغير العشوائي X كما في الجدول الآتي :

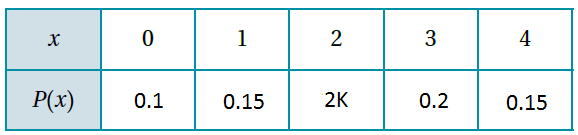
1) أجد قيمة K

2) أجد قيمة $P ( 1 \le x \le 3)$

الحل : 

1) أجد قيمة K 

لأنّ $\sum _{}P\left(x\right) = 1$	$0.1 + 0.15 + 2k + 0.2 + 0.15 = 1$
بتجميع الحدود المتشابهة	$2k + 0.6 = 1$
بطرح 0.6 من طرفي المعادلة	$2k = 0.4$
بقسمة طرفي المعادلة على 2	$\mathit{k}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{2}$

    

 

 

 

 

2) أجد قيمة $P ( 1 \le x \le 3)$

أجمع احتمالات قيم المتغير العشوائي ضمن الشرط المُحدَّد ، مع ملاحظة أنّ  $P(x=2) = 2K = 2 \times 0.2 = 0.4$

بتحديد قِيَم المتغير العشوائي ضمن الشرط المُحدَّد	$P ( 1 \le x \le 3) = P(x=1) + P(x=2) + P(x=3)$
بتعويض قِيَم الاحتمالات	$= 0.15 + 0.4 + 0.2$
بالجمع	$\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{75}$

 

 

 

 

 

 

 

 

---

 

• يُمكِن أيضًا تمثيل التوزيع الاحتمالي للمتغير العشوائي X في صورة مجموعة من الأزواج المُرتَّبة التي إحداثيات x لها مجموعة قِيَم المتغير العشوائي، وإحداثيات y لها مجموعة احتمالات الحوادث المرتبطة بقِيَم المتغير العشوائي.

 مثال :

في تجربة عشوائية ، كان التوزيع الاحتمالي للمتغير العشوائي X مُعرَّفًا على النحو الآتي :   

                                                         {(1 , 3a) , (2 ,  a) , (3 ,  a)} 

1) أجد قيمة a.

2) أُنشِئ جدول التوزيع الاحتمالي.

3) أجد $P(x< 3)$.

الحل : 

1) أجد قيمة a.

لأنّ : $\sum _{}P\left(x\right) = 1$	$3a + a + a = 1$
بتجميع الحدود المتشابهة	$5a = 1$
بقسمة طرفي المعادلة على 5	$\mathit{a}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{2}\mathbf{ }$

 

 

 

 

2) أُنشِئ جدول التوزيع الاحتمالي.

3	2	1	x
0.2	0.2	0.6	P(x)

 

 

 

3) أجد $P(x< 3)$

بتحديد قِيَم المتغير العشوائي ضمن الشرط المُحدَّد	$P ( x < 3) = P(x=2) + P(x=1)$
بتعويض قِيَم الاحتمالات	$= 0.2 + 0.6$
بالجمع	$\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{8}$

 

 

 

 

---

 

• يُمكِن حساب احتمالات قِيَم المتغير العشوائي باستعمال مبدأ العَدِّ ، والتباديل ، والتوافيق.

 مثال :

في تجربة سحب كرتين عشوائيًّا على التوالي من دون إرجاع من كيس فيه 4 كرات حمراء، و 3 كرات زرقاء، جميعها مُتماثِلة، إذا دلَّ المتغير العشوائي X على عدد الكرات الزرقاء في السحبة، فأُنشِئ جدول التوزيع الاحتمالي للمتغير العشوائي x.

الحل : 

الخطوة 1 : أجد قِيَم المتغير العشوائي.

$X = \{ 0 , 1 , 2 \}$

الخطوة 2 : أجد احتمالات قِيَم المتغير العشوائي.

0 كرة خضراء ، و كرتان حمراء	$P (x = 0) = \frac{ {}_{3}C_0 \times {}_{4}C_2}{{}_{7}C_2} = \frac{2}{7}$
1 كرة خضراء ، و  1 كرة حمراء	$P (x = 1) = \frac{ {}_{3}C_1 \times {}_{4}C_1}{{}_{7}C_2} = \frac{4}{7}$
2 كرة خضراء ، و 0 كرة حمراء	$P (x = 2) = \frac{ {}_{3}C_2 \times {}_{4}C_0}{{}_{7}C_2} = \frac{1}{7}$

 

 

 

 

 

 

 

 

الخطوة 3 : أُنشِئ جدول التوزيع الاحتمالي.

2	1	0	x
$\frac{1}{7}$	$\frac{4}{7}$	$\frac{2}{7}$	P(x)