رياضيات فصل ثاني

إثبات توازي المستقيمات وتعامدها 

أعلم أن : 

إذا قطع مستقيم مستقيمين متوازيين في المستوي نفسه فإن :

1) كل زاويتين متناظرتين متطابقتان ( مسلمة الزاويتين المتاظرتين ) 

مثال : 

 

$\mathbf{\angle }\mathbf{3}\mathbf{\cong }\mathbf{\angle }\mathbf{7}$

 $\mathbf{\angle }\mathbf{4}\mathbf{\cong }\mathbf{\angle }\mathbf{8}$ 

$\mathbf{\angle }\mathbf{5}\mathbf{\cong }\mathbf{\angle }\mathbf{1}$

$\mathbf{\angle }\mathbf{6}\mathbf{\cong }\mathbf{\angle }\mathbf{2}$                        

.......................................................

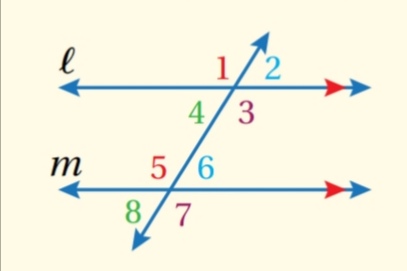
2) كل زاويتين متبادلتين داخلياً متطابقتان ( نظرية الزاويتين المتبادلتين داخلياً ) 

مثال : 

 $\mathbf{\angle }\mathbf{3}\mathbf{\cong }\mathbf{\angle }\mathbf{5}$             

$\mathbf{\angle }\mathbf{4}\mathbf{\cong }\mathbf{\angle }\mathbf{6}$                      

...................................

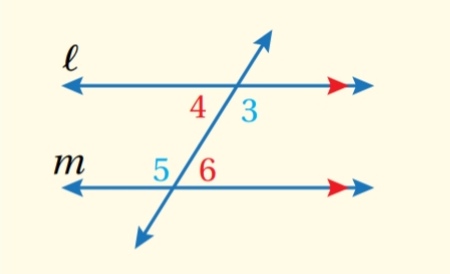
3) كل زاويتين متبادلتين خارجياً متطابقتان ( نظرية الزاويتين المتبادلتين خارجياً ) 

مثال : 

$\mathbf{\angle }\mathbf{1}\mathbf{\cong }\mathbf{\angle }\mathbf{7}$

$\mathbf{\angle }\mathbf{2}\mathbf{\cong }\mathbf{\angle }\mathbf{8}$                                 

.....................................

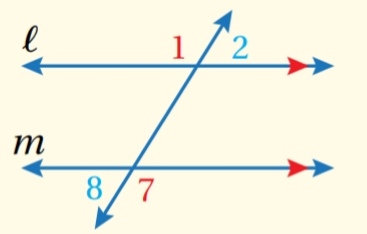
4) كل زاويتين متحالفتين متكاملتان ( نظرية الزاويتين المتحالفتين ) 

مثال : 

 $\mathbf{m}\mathbf{\angle }\mathbf{3}\mathbf{+}\mathbf{m}\mathbf{\angle }\mathbf{5}\mathbf{=}\mathbf{180}\mathbf{°}$                           

$\mathbf{m}\mathbf{\angle }\mathbf{3}\mathbf{+}\mathbf{m}\mathbf{\angle }\mathbf{6}\mathbf{=}\mathbf{180}\mathbf{°}$

..........................................................................................................................................................................................................

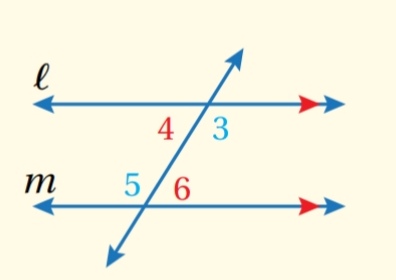
مسلمة:

عكس مسلمة الزاويتين المتناظرتين : 

إذا قطع قاطع مستقيمين ، وينتج عن التقاطع زاويتان متناظرتان متطابقتان فإن المستقيمين متوازيان .

مثال: 

إذا كانت : 

                 $\mathbf{ }\mathbf{ }\mathbf{ }\mathit{L}\mathbf{\parallel }\mathbf{m}\mathbf{ }\mathbf{ }\mathbf{فإن}\mathbf{ }\mathbf{\angle }\mathbf{2}\mathbf{\cong }\mathbf{\angle }\mathbf{6}$                                             

.....................................................................................................................................................................................................................................................................

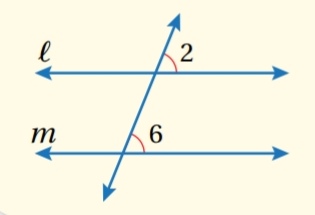
مثال ( 1 ) :

أجد قيمة x  التي تجعل     $\mathit{n}\mathbf{\parallel }\mathit{m}$                                           

                                                                  

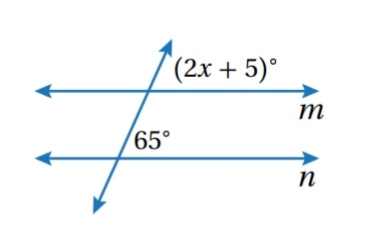
الحل :

يكون المستقيمان m و n  متوازيين إذا كانت الزاويتان المتناظرتان متطابقتين

$( 2x+ 5)=65$                         استعمل عكس مسلمة الزاويتين المتناظرتين لكتابة معادلة

$2x+ 5=65$

$2x+ 5 - 5=65- 5$

$2x=60$

$\frac{2\mathrm{x}}{2}=\frac{60}{2}$

$x=30$

إذن قيمة  x  التي تجعل المستقيمن  m و n  متوازيين تساوي  30

....................................................................................................................................................................................................................................

عكس نظريات المستقيمين المتوازيين وأزواج الزوايا:

• عكس نظرية الزاويتين المتبادلتين داخلياً :                                                                       

                                           

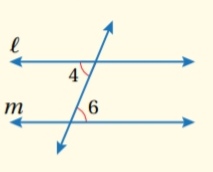
إذا قطع قاطع مستقيمين ونتج عن التقاطع زاويتان متبادلتان داخلياً متطابقتان فإن المستقيمين متوازيان.

مثال : 

إذا كانت :        $\mathit{L}\mathbf{\parallel }\mathit{m}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{فإن}\mathbf{ }\mathbf{ }\mathbf{\angle }\mathbf{4}\mathbf{ }\mathbf{\cong }\mathbf{\angle }\mathbf{6}$

..................................................................

• عكس نظرية الزاويتين المتحالفتين : 

                                        

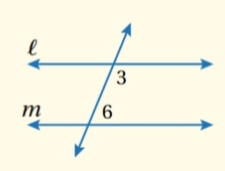
إذا قطع قاطع مستقيمن ونتج عن التقاطع زاويتان متحالفتان متكاملتان فإن المستقيمين متوازيان.

مثال: 

 إذا كانت:    $\mathit{L}\mathbf{\parallel }\mathit{m}\mathbf{ }\mathbf{ }\mathbf{فإن}\mathbf{ }\mathbf{ }\mathit{m}\mathbf{\angle }\mathbf{3}\mathbf{+}\mathit{m}\mathbf{\angle }\mathbf{6}\mathbf{ }\mathbf{=}\mathbf{180}\mathbf{°}$ 

............................................................................

• عكس نظرية الزاويتين المتبادلتين خارجياً : 

                                          

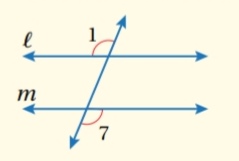
إذا قطع قاطع مستقيمين ونتج عن التقاطع زاويتان متبادلتان خارجياً متطابقتان

فإن المستقيمين متوازيان : 

مثال: 

إذا كانت :     $\mathit{L}\mathbf{ }\mathbf{\parallel }\mathbf{ }\mathit{m}\mathbf{ }\mathbf{فإن}\mathbf{ }\mathbf{ }\mathbf{\angle }\mathbf{1}\mathbf{ }\mathbf{\cong }\mathbf{ }\mathbf{\angle }\mathbf{7}$

..........................................................................................................................................................................................................

مثال ( 2 ): إثبات نظرية : 

في الشكل المجاور ، إذا كان $\mathbf{ }\mathit{g}\mathbf{\parallel }\mathit{h}\mathbf{فأثبت}\mathbf{\angle }\mathbf{4}\mathbf{\cong }\mathbf{\angle }\mathbf{5}$باستعمال المخطط السهمي:

                                                   

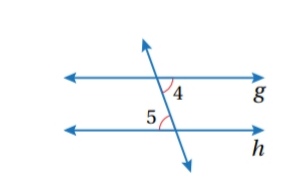
الحل: 

المعطيات:    $\mathbf{\angle }\mathbf{4}\mathbf{\cong }\mathbf{\angle }\mathbf{5}$                              

المطلوب :    $\mathit{g}\mathbf{\parallel }\mathit{h}$

               

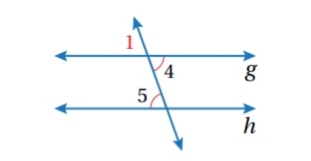
الاثبات أسمي   $\mathbf{\angle }\mathbf{1}$   التي تقابل بالرأس  $\mathbf{\angle }\mathbf{4}$

 

..........................................................................................................................................................................................................

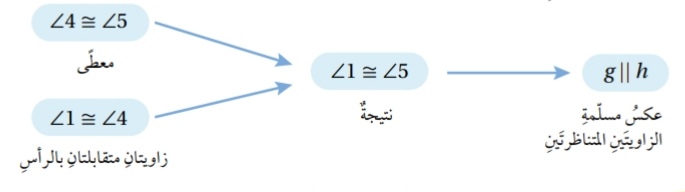
مثال ( 3 ) :

هل يمكن إثبات أن أياً من مستقيمات الشكل المجاور متوازية اعتماداً على المعطيات في كل مما يأتي ؟ 

( أبرر إجابتي باستعمال مسلمة أو نظرية )

 

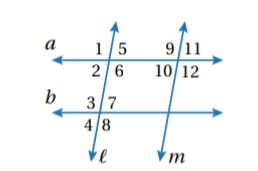
1)   $\mathbf{\angle }\mathbf{1}\mathbf{ }\mathbf{\cong }\mathbf{\angle }\mathbf{8}$ 

$\mathbf{\angle }\mathbf{8}$  و $\mathbf{\angle }\mathbf{1}$ متبادلتان خارجياً بالنسبة للمستقيمين a  و b  

وبما أن       $\mathbf{\angle }\mathbf{1}\mathbf{\cong }\mathbf{\angle }\mathbf{8}$ فإن $\mathit{a}\mathbf{\parallel }\mathit{b}$

بحسب عكس نظرية الزاويتين المتبادلتين خارجياً 

..........................................................................................................................................................................................................

2)   $\mathit{m}\mathbf{\angle }\mathbf{5}\mathbf{+}\mathit{m}\mathbf{\angle }\mathbf{9}\mathbf{=}\mathbf{180}\mathbf{°}$

   $\mathbf{\angle }\mathbf{5}\mathit{و}\mathbf{ }\mathbf{\angle }\mathbf{9}$  متحالفتان بالنسبة للمستقيمين L  و m

وبما أن $\mathit{m}\mathbf{\angle }\mathbf{5}\mathbf{+}\mathit{m}\mathbf{\angle }\mathbf{9}\mathbf{ }\mathbf{=}\mathbf{180}\mathbf{°}$ فإن $\mathit{L}\mathbf{\parallel }\mathit{m}$

بحسب عكس نظرية الزاويتين المتحالفتين.

..........................................................................................................................................................................................................

نظرية : 

نظرية الزاويتين المتجاورتين المتطابقين: 

                                                                                                            

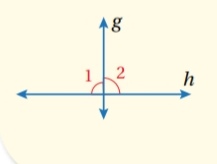
إذا تقاطع مستقيمان لتشكيل زاويتين متجاورتين متطابقتين فإن المستقيمين متعامدان .

مثال:       $\mathbf{\angle }\mathbf{1}\mathbf{\cong }\mathbf{\angle }\mathbf{2}$

فإن       $\mathit{g}\mathbf{\perp }\mathit{h}$

..........................................................................................................................................................................................................

نظرية القاطع العمودي : 

إذا كان مستقيم عمودياً على أحد مستقيمين متوازيين

فإنه يكون عمودياً على المستقيم الآخر

 

$\mathit{h}\mathbf{\parallel }\mathit{k}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{كان}\mathbf{ }\mathbf{إذا}\mathbf{ }\mathbf{:}\mathbf{ }\mathbf{مثال}$                                                          

                                   $\mathit{j}\mathbf{\perp }\mathit{h}\mathbf{ }\mathbf{ }\mathit{و}$

                               $\mathit{j}\mathbf{\perp }\mathit{k}\mathbf{ }\mathbf{ }\mathbf{فإن}$

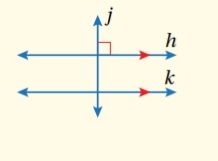
عكس نظرية القاطع العمودي : 

إذا قطع قاطع مستقيمين وكان عمودياً على كل منهما 

فإن المستقيمين متوازيان

مثال: 

$\mathit{p}\mathbf{\perp }\mathit{n}\mathbf{ }\mathit{و}\mathbf{ }\mathbf{ }\mathit{p}\mathbf{\perp }\mathit{m}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{كان}\mathbf{ }\mathbf{إذا}$                                                          

                      $\mathit{m}\mathbf{\parallel }\mathit{n}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{فإن}$

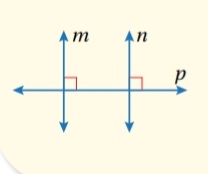
مثال ( 4 ) : 

إثبات نظرية : 

استعمل المعلومات المعطاة في الشكل المجاور 

لأثبت أن $\mathit{r}\mathbf{ }\mathbf{\parallel }\mathit{s}$  باستعمال البرهان ذي العمودين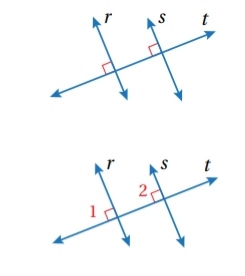                                                                      

الحل: 

 

المبررات	العبارات
1) معطى	1) $\mathbf{قائمتان}\mathbf{ }\mathbf{\angle }\mathbf{2}\mathbf{ }\mathit{و}\mathbf{ }\mathbf{\angle }\mathbf{1}$
2) الزوايا القائمة متطابقة	2) $\mathbf{\angle }\mathbf{1}\mathbf{\cong }\mathbf{\angle }\mathbf{2}$
3) عكس مسلمة الزاويتين المتناظرتين	3) $\mathit{r}\mathbf{\parallel }\mathit{s}$

..............................................................................................................................................................................................................................................................................