مفاهيم أساسية :
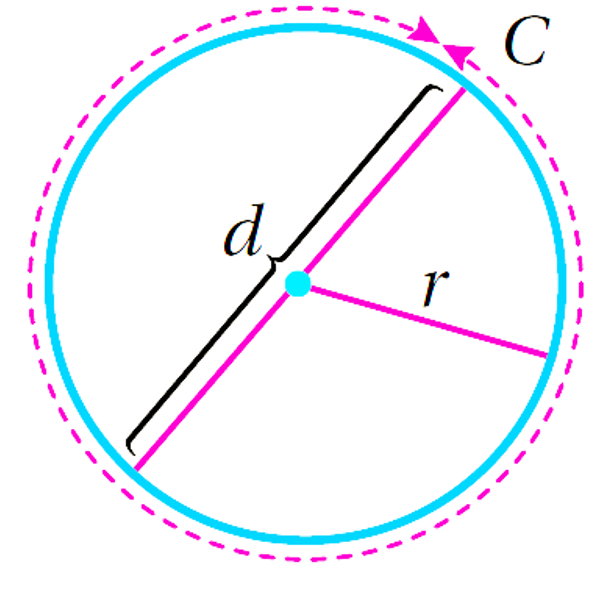
إن النسبةَ بين محيطِ أيِّ دائرةٍ إلى قُطْرِها نسبة لانهائية وتساوي تقريبًا 3.14، ,وتسمى النسبةَ التقريبيةَ pi ويرمز لها بالرمز وتُستعمَلُ هذهِ النسبةُ لإيجادِ محيطِ الدائرةِ وَهُوَ المسافةُ حولَها.
محيطُ الدائرةِ (C) يساوي ناتجَ ضربِ طولِ القُطْرِ (d) في () أو يساوي مِثْلَيْ ناتجِ ضربِ طولِ نصفِ القُطْرِ (r) في ()
مثال 1:أَجِدُ محيطَ كلِّ دائرةٍ ممّا يأتي، وَأستعملُ الآلةَ الحاسبةَ لأتحقّقَ مِنْ صحةِ إجابتي
1)
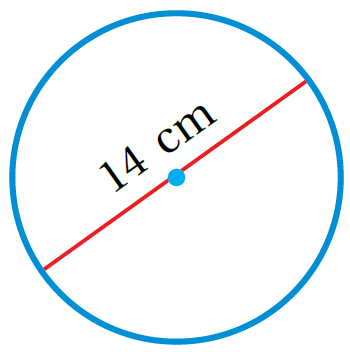
بما أنَّ 14 أحدُ مضاعفاتِ 7، إذنْ، أستعملُ
صيغة محيط الدائرة
أعوض قيمة القطر d وقيمة التقريبية ، ثم أجد الناتج
إذنْ، محيطُ الدائرةِ يساوي 44cm تقريباً
أستعملُ الآلةَ الحاسبةَ لأتحقّقَ مِنْ صحةِ إجابتي على النحوِ الآتي:

وَعندَ تقريبِ الإجابةِ لِقربِ جزءٍ مِنْ عشرةٍ، يكونُ المحيطُ 44cm تقريبًا. إذنْ، إجابتي صحيحةٌ.
2)
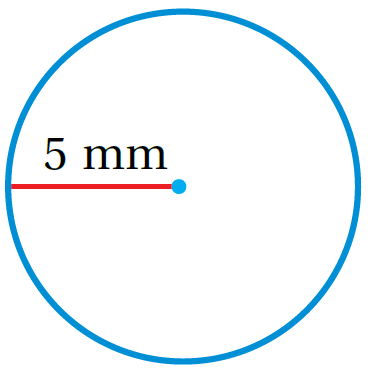
صيغة محيط الدائرة
أعوض قيمة نصف القطر r وقيمة التقريبية ،ثم أجد الناتج
إذنْ، محيطُ الدائرةِ يساوي 31.4mm تقريباً
أستعملُ الآلةَ الحاسبةَ لأتحقّقَ مِنْ صحةِ إجابتي على النحوِ الآتي:

وَعندَ تقريبِ الإجابةِ لأقربِ جزءٍ مِنْ عشرةٍ، يكونُ المحيطُ 31.4mm تقريبًا. إذنْ، إجابتي صحيحةٌ
يُمكنُ إيجادُ طولِ نصفِ قُطْرِ الدائرةِ أَوْ طولِ قُطْرِها إذا علمْتُ محيطَها، بِاستعمالِ خُطواتِ حلِّ المعادَلةِ.
مثال 2:
1) أَجِدُ طولَ نصفِ قُطْرِ دائرةٍ محيطُها 18.84cm أستعملُ 3.14
صيغة محيط الدائرة
أعوض محيط الدائرة و قيمة التقريبية
أقسم الطرفين على 2×3.14
إذنْ، طولُ نصف قُطْرِ الدائرةِ يساوي 3cm
2) أَجِدُ طولَ قُطْرِ دائرةٍ محيطُها 62.8cm أستعملُ 3.14
صيغة محيط الدائرة
أعوض محيط الدائرة و قيمة التقريبية
بقسمة الطرفين على 3.14 أجد طول نصف القطر
20 m إذنْ، طولُ قُطْرِ الدائرةِ يساوي
يُمكنُ استعمالُ قانونِ محيطِ الدائرةِ في مواقفَ حياتيةٍ متنوعةٍ وَكثيرةٍ.
مثال 3: منَ الحياةِ: دوارٌ مروريٌّ: تحركَتْ حافلةٌ حَولَ دوّارٍ مُروريٍّ في مسارٍ دائريٍّ طولُ قطرهِ 30m أَجِدُ المسافةَ الّتي قطعَتْها الحافلةُ بعدَ أنْ سارَتْ حولَ الدوارِ المروريِّ مرةً واحدةً.
المسافةُ الّتي قطعَتْها الحافلةُ تساوي محيطَ المسارِ الدائريِّ، وَبما أنَّه على شكلِ دائرةٍ فَينبغي أَنْ أَجِدَ محيطَ الدائرةِ.
صيغة محيط الدائرة
بتعويض قيمة قطر المسار الدائري وقيمة التقريبية
إذنْ، المسافةُ الّتي قطعَتْها الحافلةُ تساوي 94.2m تقريبا