(SSS, SAS, HL) تطابقُ المثلثاتِ

المسلّمة : عبارةٌ رياضيةٌ تُقبلُ على أنَّها صحيحةٌ مِنْ دونِ برهانٍ.

تذكير: إذا كانَتِ الأضلاعُ المتناظرةُ في شكلَينِ هندسيَّينِ متطابقةً، وزواياهُما المتناظرةُ متطابقةً، فإنَّ الشكلَينِ متطابقانِ والعكس صحيح.

توضيح : 

 

 

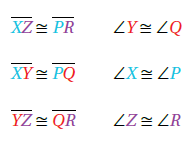
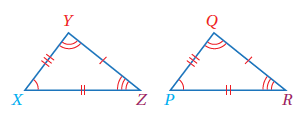
حيث :  

 $\angle$  تمثل الزاوية

$\cong$ تمثل إشارة التطابق.

لكنَّ هذِهِ المعلوماتِ أكثرُ مِنْ كافيةٍ لإثباتِ تطابقِ مثلثَينِ . إِذْ يمكنُ إثباتُ ذلكَ باستعمالِ خمس مسلمات ونظريات لا نحتاج فيها كل العناصر السابقة بل نحتاج أجزاء منها : كتطابق المثلثين بثلاثة أضلاع SSS أو بضلعين وزاوية محصورة SAS ...

---

مسلَّمة :  إذا تطابقَتْ أضلاعُ مثلثٍ مَعَ الأضلاعِ المناظرةِ لَها في مثلثٍ آخَرَ : فإنَّ المثلثَينِ متطابقان وتُختصَرُ هذهِ الحالةُ بالرمزِ  SSS .

إذا كان  :  $$\begin{gathered} \overline{\mathbf{A}\mathbf{B}}\mathbf{\cong }\overline{\mathbf{R}\mathbf{S}\mathbf{ }} \\ \overline{\mathbf{B}\mathbf{C}}\mathbf{\cong }\overline{\mathbf{S}\mathbf{T}\mathbf{ }} \\ \overline{\mathbf{A}\mathbf{C}}\mathbf{\cong }\overline{\mathbf{R}\mathbf{T}\mathbf{ }} \end{gathered}$$  فإن $\mathbf{∆}\mathit{A}\mathit{B}\mathit{C}\mathbf{\cong }\mathbf{ }\mathbf{∆}\mathit{R}\mathi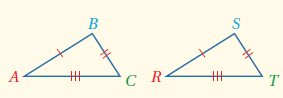t{S}\mathit{T}$ .

---

ملاحظة : نستخدم طريقتين لإثبات التطابق  : 

1- طريقة البرهان السهمي : هُوَ برهانٌ تُستعملُ فيهِ عباراتٌ مكتوبةٌ في مستطيلاتٍ، وأسهمٌ تبيّنُ التسلسلَ المنطقيَّ لهذهِ العباراتِ، ويُكتبُ أسفلَ كلِّ مستطيلٍ السببُ الّذي يبرّرُ العبارةَ المكتوبةَ داخلَهُ.

2-طريقة البرهان ذي  العمودين : وَهُوَ برهانٌ تُكتبُ فيهِ العباراتُ مرتبةً في عمودٍ، والتبريراتُ في عمودٍ مُوازٍ لَهُ.

---

مثال 1 : أثبتُ أنَّ المثلثَينِ $\mathbf{∆}\mathit{C}\mathit{B}\mathit{D}$ و  $\mathbf{∆}\mathit{A}\mathit{B}\mathit{D}$  المبيّنَينِ في الشكلِ المجاورِ متطابقانِ باستعمالِ البرهانِ السهميِّ.

---

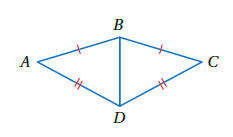
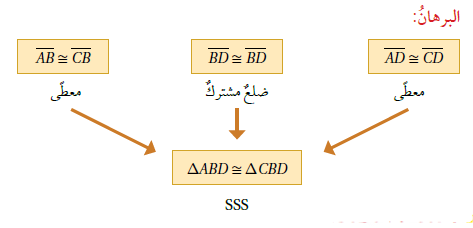
ملاحظة :  تُسمّى الزاويةُ المتكوّنةُ مِنْ ضلعَينِ متجاورَينِ في مضلعٍ الزاويةَ المحصورةَ

---

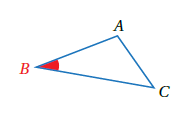
مسلَّمة : إذا تطابقَ ضلعانِ والزاويةُ المحصورةُ بينَهُما في مثلثٍ مَعَ نظائِرها في مثلثٍ آخرَ، فإنَّ المثلثَين متطابقانِ. وتُختصَرُ هذهِ الحالةُ بالرمزِ  SAS.

إذا كان  : $$\begin{gathered} \overline{\mathbf{ }\mathbf{A}\mathbf{B}}\mathbf{\cong }\overline{\mathbf{R}\mathbf{S}\mathbf{ }} \\ \mathbf{\angle }\mathit{A}\mathbf{\cong }\mathbf{\angle }\mathit{R} \\ \overline{\mathbf{ }\mathbf{A}\mathbf{C}}\mathbf{\cong }\overline{\mathbf{R}\mathbf{T}\mathbf{ }} \end{gathered}$$  فإن : $\mathbf{∆}\mathit{A}\mathit{B}\mathit{C}\mathbf{\cong }\mathbf{ }\mathbf{∆}\mathit{R}\mathi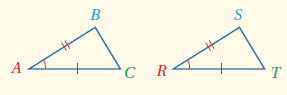t{S}\mathit{T}$
 

---

مثال 2 : أثبتُ أنَّ المثلثَينِ $∆CDA$ و $∆ABC$   المبيّنَينِ في الشكلِ المجاورِ متطابقانِ باستعمالِ البرهان ذي العمودين.

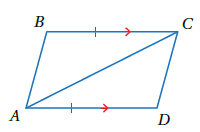البرهان :

العباراتُ	المبرراتُ
$\overline{\mathbf{B}\mathbf{C}}\mathbf{\cong }\overline{\mathbf{D}\mathbf{A}}$	معطى
$\overline{\mathbf{BC}}\parallel \overline{\mathbf{DA}}$	معطى
$\mathbf{\angle }\mathit{B}\mathit{C}\mathit{A}\mathbf{ }\mathbf{\cong }\mathbf{\angle }\mathit{D}\mathit{A}\mathit{C}$	زاويتان متبادلتان داخلياً
$\overline{\mathbf{AC}}\mathbf{\cong }\overline{\mathbf{AC}}$	ضلع مشترك
$\mathbf{∆}\mathit{A}\mathit{B}\mathit{C}\mathbf{\cong }\mathbf{△}\mathit{C}\mathit{D}\mathit{A}$	SAS

 

---

مثال 3 : من الحياة 

عمارةٌ: صمّمَ مهندسٌ معماريٌّ النافذةَ المجاورةَ. إذا كانَ $\overline{\mathbf{D}\mathbf{A}}\mathbf{\cong }\mathbf{ }\overline{\mathbf{D}\mathbf{G}}$ و $\mathbf{\angle }\mathit{A}\mathit{D}\mathit{R}\mathbf{ }\mathbf{\cong }\mathbf{ }\mathbf{\angle }\mathit{G}\mathit{D}\mathit{R}$  فأكتبُ برهانًا ذا عمودَينِ؛ لإثباتِ أنَّ $\mathbf{△}\mathit{D}\mathit{R}\mathit{A}\mathbf{\cong }\mathbf{ }\mathit{D}\mathit{R}\mathit{G}$.

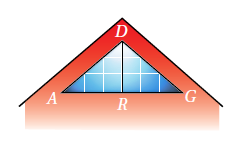
البرهان :

 

العبارات	المبررات
$\overline{\mathbf{DA}}\mathbf{\cong }\overline{\mathbf{DG}}$	معطى
$\mathbf{\angle }\mathit{A}\mathit{D}\mathit{R}\mathbf{ }\mathbf{\cong }\mathbf{\angle }\mathit{G}\mathit{D}\mathit{R}$	معطى
$\overline{\mathbf{DR}}\mathbf{\cong }\overline{\mathbf{DR}}$	ضلع مشترك
$\mathbf{∆}\mathit{D}\mathit{R}\mathit{A}\mathbf{\cong }\mathbf{△}\mathit{D}\mathit{R}\mathit{G}$	SAS

 

---

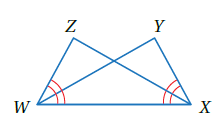
مثال 4 : في الشكلِ المجاورِ، إذا علمْتُ أنَّ $\mathbf{\angle }\mathit{Z}\mathit{W}\mathit{X}\mathbf{ }\mathbf{\cong }\mathbf{\angle }\mathit{Y}\mathit{X}\mathit{W}$ ,  $\overline{\mathbf{Z}\mathbf{W}}\mathbf{\cong }\overline{\mathbf{Y}\mathbf{X}}$ فأثبت أنّ $\overline{\mathbf{ZX}}\mathbf{\cong }\overline{\mathbf{YW}}$ باستعمال البرهان السهمي .

 

---

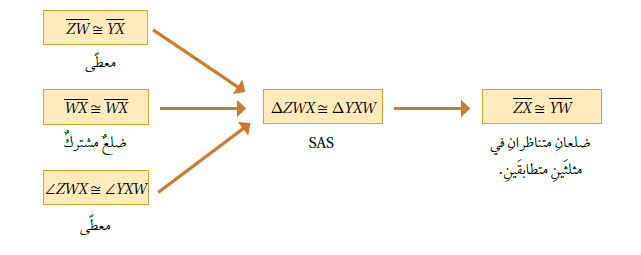
أتعلّم :

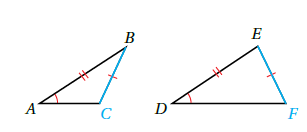
يبيّنُ الشكلُ المجاورُ مثلثَينِ فيهِما ضلعانِ متناظرانِ متطابقانِ وزاويةٌ غيرُمحصورةٍ تُطابقُ زاويةً غيرَ محصورةٍ في المثلثِ الآخَرِ. ولكنَّ المثلثَينِ غيرُ متطابقَينِ. وَمِنْ هنا يتبيّنُ أنَّ حالةَ ضلعَينِ وزاويةٍ غيرِ محصورةٍ بينَهُما غيرُ فعّالةٍ، إلا أنَّهُ يمكنُ استعمالُها في إثباتِ تطابقِ مثلثَينِ قائمَيِ الزاويةِ؛ إذا تطابقَ الوتَرانِ، وتطابقَ ساقانِ في المثلثَينِ.

ملاحظة : إذا تم إثبات صحة عبارة أو تخمين عندها تسمى نظرية.

 

 

 

---

نظرية :   إذا طابقَ وَترٌ وساقٌ في مثلثٍ قائمِ الزاويةِ وَترًا وساقًا في مثلثٍ قائمٍ آخَرَ، فإنَّ المثلثَينِ متطابقانِ. وتُختصَرُ هذهِ الحالةُ بالرمزِ HL .

 

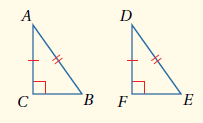إذا كان : $$\begin{gathered} \overline{\mathbf{AB}}\mathbf{\cong }\overline{\mathbf{DE}} \\ \overline{\mathbf{AC}}\mathbf{\cong }\mathbf{ }\overline{\mathbf{DF}} \end{gathered}$$ فإن : $\mathbf{∆}\mathit{A}\mathit{B}\mathit{C}\mathbf{ }\mathbf{\cong }\mathbf{ }\mathbf{∆}\mathit{D}\mathit{E}\mathit{F}$

 

 

---

مثال 5 : في الشكلِ المجاورِ، إذا علمْتُ أنَّ $\overline{\mathbf{X}\mathbf{Y}}\mathbf{\perp }\overline{\mathbf{Y}\mathbf{Z}}\mathbf{ }\mathbf{,}\mathbf{ }\overline{\mathbf{W}\mathbf{Z}}\mathbf{\perp }\overline{\mathbf{Z}\mathbf{Y}}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{ }\overline{\mathbf{W}\mathbf{Y}}\mathbf{\cong }\overline{\mathbf{X}\mathbf{Z}}$ فأكتبُ برهانًا ذا عمودَينِ؛ لإثباتِ أنَّ $\mathbf{∆}\mathit{W}\mathit{Y}\mathit{Z}\mathbf{ }\mathbf{\cong }\mathbf{ }\mathbf{∆}\mathit{X}\mathit{Z}\mathit{Y}$.

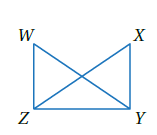
العبارات	المبررات
$\mathbf{ }\overline{\mathbf{WY}}\mathbf{\cong }\overline{\mathbf{XZ}}$	معطى
$\overline{\mathbf{XY}}\mathbf{\perp }\overline{\mathbf{YZ}}\mathbf{ }\mathbf{,}\mathbf{ }\overline{\mathbf{WZ}}\mathbf{\perp }\overline{\mathbf{ZY}}$	معطى
$\mathbf{\angle }\mathit{W}\mathit{Z}\mathit{Y}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{\angle }\mathit{X}\mathit{Y}\mathit{Z}$ زاويتان قائمتان	تعريف المستقيمات المتعامدة
$\mathbf{∆}\mathit{W}\mathit{Y}\mathit{Z}\mathbf{,}\mathbf{ }\mathbf{∆}\mathit{X}\mathit{Z}\mathit{Y}$ مثلثان قائما الزاوية	تعريف المثلث القائم الزاوية
$\overline{\mathbf{Z}\mathbf{Y}}\mathbf{\cong }\overline{\mathbf{Z}\mathbf{Y}}$	ضلع مشترك
$\mathbf{∆}\mathit{W}\mathit{Y}\mathit{Z}\mathbf{ }\mathbf{\cong }\mathbf{ }\mathbf{∆}\mathit{X}\mathit{Z}\mathit{Y}$	HL

 

---