مُنصِّفاتٌ في المُثلَّثِ

مُنصِّفاتٌ في المُثلَّثِ

Bisectors in Triangle

فكرةُ الدرسِ : • تعرُّفُ نظريةِ المُنصِّفاتِ العموديةِ للمُثلَّثِ، واستعمالُها لإيجادِ قياساتٍ مجهولةٍ.

                      • تعرُّفُ نظريةِ مُنصِّفاتِ زوايا المُثلَّثِ، واستعمالُها لإيجادِ قياساتٍ مجهولةٍ.

 

أولًا : المُنصِّفُ العموديُّ

المُنصِّفُ العموديُّ لقطعةٍ مستقيمةٍ هوَ مستقيمٌ عموديٌّ على القطعةِ المستقيمةِ عندَ نقطةِ منتصفِها.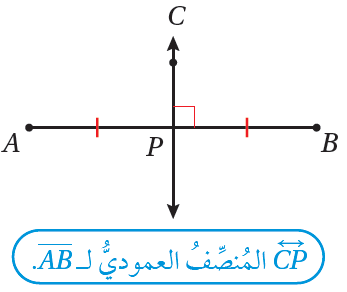

 

•• للمُنصِّفِ العموديِّ بعضُ الخصائصِ التي تُمثِّلُها النظريتانِ الآتيتانِ.

نظريتانِ (المُنصِّفُ العموديُّ)

1 ـ نظريةُ المُنصِّفِ العموديِّ : كلُّ نقطةٍ على المُنصِّفِ العموديِّ لقطعةٍ مستقيمةٍ تكونُ على بُعْدينِ متساويينِ منْ طرفيِ القطعةِ المستقيمةِ.  مثال : إذا كانَ  Ɩ مُنصِّفًا عموديًّا لـ $\overline{AB}$ ، فإنَّ $AX = BX$، لأيِّ نقطةٍ $X$ على Ɩ
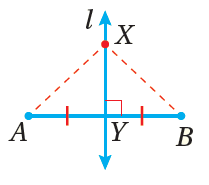2 ـ · عكسُ نظريةِ المُنصِّفِ العموديِّ :  كلُّ نقطةٍ على بُعْدينِ متساويينِ منْ طرفيْ قطعةٍ مستقيمةٍ تقعُ على المُنصِّفِ العموديِّ لتلكَ القطعةِ. مثال : إذا كانَ $AX = BX$ ، و Ɩ مُنصِّفًا عموديًّا لـ $\overline{AB}$ ، فإنَّ $X$ تقعُ على Ɩ

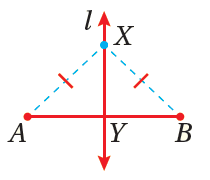مثال 1 : 

مُعتمدًا الرسم المجاور : 1) أجد طول $\overline{LT}$

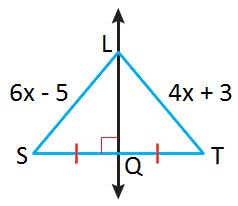الحل  : 

1) طول $\overline{LT}$

الخطوةُ 1 : أجدُ قيمةَ x

نظريةُ المُنصِّفِ العموديِّ	$LS=LT$
بالتعويضِ	$6x - 5 = 4x + 3$
بحَلِّ المعادلةِ	$x = 4$

الخطوةُ 2 : أجدُ طول $\overline{LT}$

طول$LT$ بدلالة $x$	$LT = 4x + 3$
بتعويض $x = 4$	$LT = 4\left(2\right) + 3$
بالتبسيط	$LT = 19$

---

مثال 2 :  في الرسم المجاور ، إذا كان $HJ = 4.2 cm$ ، فما طول $\overline{RJ}$

 

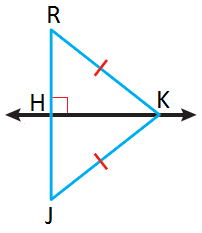الحل  : 

بما أنَّ $RK = JK$ ، و $H$ عموديٌّ على $RJ$ ، فإنَّ $H$ مُنصِّفٌ عموديٌّ لـ $RJ$ بحسبِ عكسِ نظريةِ المُنصِّفِ العموديِّ : 

تعريفُ المُنصِّفِ العموديِّ	$RJ = 2 HJ$
بالتعويضِ	$RJ = 2 (4.2)$
بالتبسيط	$RJ = 8.4 cm$

---

•• تعلَّمتُ سابقًا أنّهُ يُمكن إيجاد معادلة أيِّ مستقيم إذا عُلم ميلُهُ ونقطةٌ يمرُّ بها. ومنْ ثَمّ، فإنّهُ يُمكن إيجاد معادلة المُنصِّف العموديِّ كما في المثال الآتي.

مثال 3 : 

أجدُ معادلةَ المُنصِّفِ العموديِّ للقطعةِ المستقيمةِ AB ، حيثُ : ( 6 , B(-2 ، و ( 2 , .A(4

الحل  : 

الخطوةُ 1 : أجد ميل المُنصف العمودي 

ميلُ المُنصِّفِ العموديِّ يساوي سالبَ مقلوبِ ميلِ القطعةِ المستقيمةِ نفسِها ؛ لذا أجدُ أوَّلًا ميلَ القطعةِ المستقيمةِ : 

صيغةُ الميلِ	$m =\frac{y_2 - y_1}{x_2 - x_1}$
بتعويضِ $(x_1 , y_1) = (4 , 2) , (x_2 , y_2) = (-2 , 6)$	$m =\frac{6 - 2}{-2 -4}$
بالتبسيطِ	$m = -\frac{2}{3}$

إذنْ ، ميلُ المُنصِّفِ العموديِّ هوَ سالبُ مقلوبِ ميلِ $AB$ ، ويساوي $\frac{3}{2}$.

الخطوةُ 2: أجدُ نقطةَ منتصفِ القطعةِ المستقيمةِ $\overline{AB}$

صيغةُ نقطةِ المنتصفِ في المستوى الإحداثيِّ	$M (\frac{x_1 + x_2}{2} , \frac{y_1 + y_2}{2})$
بتعويضِ $(x_1 , y_1) = (4 , 2) , (x_2 , y_2) = (-2 , 6)$	$M (\frac{4 +(-2)}{2} , \frac{2 + 6}{2})$
بالتبسيطِ	$M (1 , 4)$

إذنْ، إحداثيّا النقطةِ $M$ الواقعةِ منتصفَ $\overline{AB}$ ، هما : $(1 , 4)$.

الخطوةُ 3 : أجدُ معادلةَ المُنصِّفِ العموديِّ.

صيغةُ الميلِ ونقطةٍ	$y - y_1 = m (x - x_1)$
بتعويضِ  $(x_1 , y_1) = (1 , 4) , m = \frac{3}{2}$	$y - 4 = \frac{3}{2} (x - 1)$
بالتبسيطِ، وإعادةِ ترتيبِ المعادلةِ	$y = 1.5 x + 2.5$

---

ثانيًا : المُنصِّفاتُ العموديةُ للمُثلَّثِ، ومركزُ الدائرةِ الخارجيةِ

إذا تلاقَتْ ثلاثةُ مستقيماتٍ أوْ أكثرُ في نقطةٍ مُشترَكةٍ، فإنَّ هذهِ المستقيماتِ تُسمّى مستقيماتٍ مُتلاقِيةً، وتُسمّى النقطةُ التي تلتقي فيها

المستقيماتُ نقطةَ التلاقي.

•• بما أنَّ للمُثلَّثِ ثلاثةَ أضلاعٍ، فإنَّ لهُ ثلاثةَ مُنصِّفاتٍ عموديةٍ تلتقي في نقطةٍ واحدةٍ كما تُبيِّنُ النظريةُ الآتيةُ.

 

نظريةٌ (المُنصِّفاتُ العموديةُ للمُثلَّثِ)

تلتقي المُنصِّفاتُ العموديةُ لأضلاعِ مُثلَّثٍ في نقطةٍ لها البُعْدُ نفسُهُ عنْ كلٍّ منْ رؤوسِ المُثلَّثِ. مثالٌ : إذا كانَتْ $\overline{PJ} , \overline{PL} , \overline{PK}$ هيَ المُنصِّفاتِ العموديةَ لـ $△ABC$ ، وكانَتِ النقطةُ $P$ هيَ نقطةَ تلاقيها ، فإنَّ $PA = PB = PC$ .

 

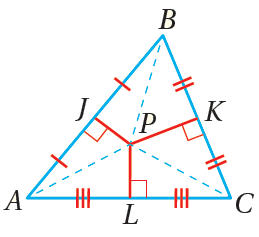•• أتعلَّمُ :  يوجدُ فرقٌ بينَ المُنصِّفِ العموديِّ للمُثلَّثِ والقطعةِ المُنصِّفةِ في المُثلَّثِ. فالقطعةُ المُنصِّفةُ تُنصِّفُ الضلعينِ اللذينِ يتقاطعانِ معها، ولا يكونُ التقاطعُ عموديًّا بالضرورةِ. أمّا المُنصِّفُ العموديُّ فهوَ مُنصِّفٌ لضلعٍ واحدٍ في المُثلَّثِ، وهوَ عموديٌّ بالضرورةِ على ذلكَ الضلعِ.

 

•• نقطةُ تلاقي المُنصِّفاتِ العموديةِ لأضلاعِ مُثلَّثٍ ما هيَ مركزُ الدائرةِ الخارجيةِ للمُثلَّثِ ؛ وهيَ دائرةٌ تمرُّ برؤوسِ المُثلَّثِ جميعِها ؛ إذْ إنَّ نقطةَ تلاقي المُنصِّفاتِ العموديةِ لأضلاعِ مُثلَّثٍ ما تبعدُ المسافةَ نفسَها عنْ كلٍّ منْ رؤوسِهِ؛ لذا فهيَ مركزٌ للدائرةِ الخارجيةِ.

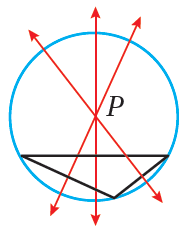
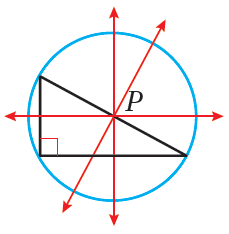
يعتمدُ موقعُ مركزِ الدائرةِ الخارجيةِ للمُثلَّثِ على نوعِ المُثلَّثِ كما في الأشكالِ الآتيةِ :

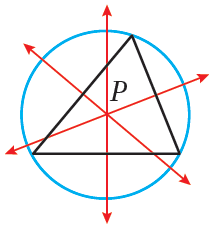مُثلَّثٌ مُنفرِجُ الزاويةِ، وفيهِ   تقعُ P خارجَ المُثلَّثِ.	مُثلَّثٌ قائمُ الزاويةِ، وفيهِ   تقعُ P على وترِ المُثلَّثِ.	مُثلَّثٌ حادُّ الزوايا، وفيهِ   تقعُ P داخلَ المُثلَّثِ.

---

مثال 4 : 

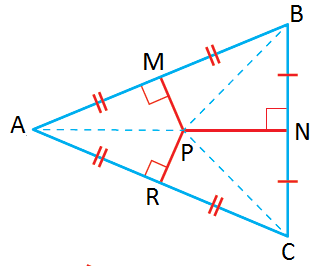
إذا كانَتِ النقطةُ $P$ هيَ مركزَ الدائرةِ الخارجيةِ لـ $\Delta ABC$ في الشكلِ المُجاوِرِ ، وكان $PC = 15 cm , PM = 7 cm$ ، فأجدُ كُلًّ ممّا يأتي : 1) طول $\overline{PA}$ 2) طول $\overline{AM}$

الحل  : 

1) طول $\overline{PA}$

نظريةُ المُنصِّفاتِ العموديةِ للمُثلَّثِ	$PA = PC$
بتعويض $PC = 15$	$PA = 15 cm$

2) طول $\overline{AM}$

نظريةُ فيثاغورس	${\left(PB\right)}^2 = {\left(PM\right)}^2 + {\left(MB\right)}^2$
بتعويضِ $PB = 15 , PM = 7$	${\left(15\right)}^2 = {\left(7\right)}^2 + {\left(MB\right)}^2$
بإيجادِ القوى	$225= 49 + {\left(MB\right)}^2$
بطرحِ49 منْ طرفيِ المعادلةِ	${\left(MP\right)}^2 = 176$
بأخذِ الجذرِ التربيعيِّ لطرفيِ المعادلةِ	$MP = \pm \sqrt{176}$

بما أنَّ الطولَ لا يُمكِنُ أنْ يكونَ سالبًا، فإنَّ $MP = \sqrt{176}$

$AM = MP$  ، إذن $AM = \sqrt{176}$

---

ثالثًا : مُنصِّفُ الزاويةِ  

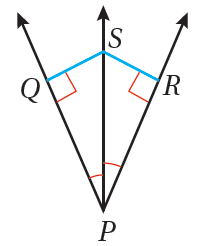
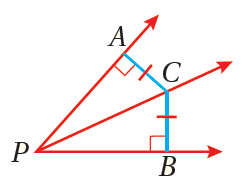
تعلم  أنَّ مُنصِّفَ الزاويةِ هو شعاعٌ يُقسِّمُ الزاويةَ إلى زاويتينِ مُتطابِقتينِ ، وتعلَّمْتُ أيضًا أنّ البُعْدَ بينَ مستقيمٍ ونقطةٍ لا تقعُ عليْهِ هوَ طولُ القطعةِ المستقيمةِ العموديةِ على المستقيمِ منْ تلكَ النقطةِ. ومنْ ثَمَّ، فإنَّ PS في الشكلِ المُجاوِرِ مُنصِّفٌ لـ $\angle QPR$ ، وإنَّ البُعْدَ بينَ النقطةِ $S$ و $\overrightarrow{PQ}$ هوَ $SQ$.

نظريتانِ (مُنصِّفُ الزاويةِ)

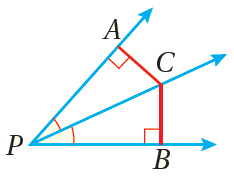
1) نظريةُ مُنصِّفِ الزاويةِ: كلُّ نقطةٍ على مُنصِّفِ الزاويةِ تكونُ على بُعْدينِ متساويينِ منْ ضلعيْها. مثال : إذا كانَ $PC$ مُنصِّفًا لـ$\angle APB$، وكانَ$CA \perp PA , CB \perp PB$ ، فإنَّ $CA = CB$
2) عكسُ نظريةِ مُنصِّفِ الزاويةِ: إذا وقعَتْ نقطةٌ داخلَ زاويةٍ، وكانَتْ على بُعْدينِ متساويينِ منْ ضلعيْها، فإنَّها تقعُ على مُنصِّفِ الزاويةِ. مثال : إذا كانَ $CA = CB , CA \perp PA , CB \perp PB$ ، فإنَّ $PC$ مُنصِّفٌ لـ $\angle APB$

مثال 5: 

استخدم  المعلومات المعطاةَ في الشكل المُجاور  لإيجاد 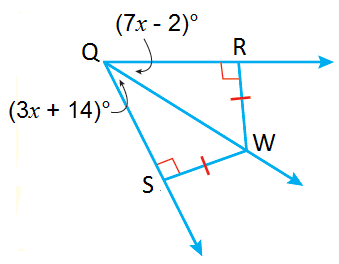$m\angle RQW$

الحل:

الخطوةُ 1: أجدُ قيمةَ $x$

عكسُ نظريةِ مُنصِّفِ الزاويةِ	$\angle SQW \cong \angle RQW$
تعريفُ تطابقِ الزوايا	$m\angle SQW = m\angle RQW$
بالتعويضِ	$3x + 14 = 7x - 2$
بحَلِّ المعادلةِ لـ$x$	$x = 4$

الخطوةُ 2 : أجدُ $m\angle RQW$

معطى	$m\angle RQW = (7x - 2)°$
بتعويضِ $x = 2$	$m\angle RQW = \left(7\right(4) - 2)°$
بالتبسيطِ	$m\angle RQW = 26°$

---

رابعًا : مُنصِّفاتُ زوايا المُثلَّثِ ، ومركزُ الدائرةِ الداخليةِ للمُثلَّثِ

بما أنَّ للمُثلَّثِ ثلاثَ زوايا، فإنَّ لهُ ثلاثةَ مُنصِّفاتٍ للزوايا تلتقي في نقطةٍ واحدةٍ كما تُبيِّنُ النظريةُ الآتيةُ.

نظريةٌ (مُنصِّفاتُ زوايا المُثلَّثِ)

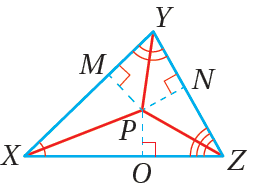
تلتقي مُنصِّفاتُ زوايا المُثلَّثِ في نقطةٍ لها البُعْدُ نفسُهُ عنْ كلٍّ منْ أضلاعِ المُثلَّثِ. مثال : إذا كانَتْ $\overline{PX} , \overline{PY}, \overline{PZ}$ هيَ مُنصِّفاتِ زوايا $△XYZ$ ، وكانَتِ النقطةُ $P$ هيَ نقطةَ تلاقيها، فإنَّ $PM = PN = PO$.

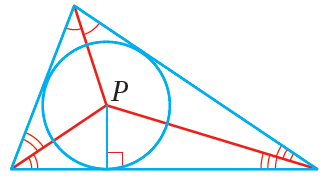
•• نقطةُ تلاقي مُنصِّفاتِ زوايا المُثلَّثِ هيَ مركزُ الدائرةِ الداخليةِ للمُثلَّثِ وهيَ دائرةٌ تمسُّ أضلاعَ المُثلَّثِ جميعَها ؛ ذلكَ أنَّ نقطةَ تلاقي مُنصِّفاتِ زوايا المُثلَّثِ تبعدُ المسافةَ نفسَها عنْ كلٍّ منْ أضلاعِهِ ؛ ما يعني أنَّها مركزُ الدائرةِ الداخليةِ.

مثال 6 : 

أستخدم المعلومات المُعطاة في الشكل المُجاوِر  لإيجاد MV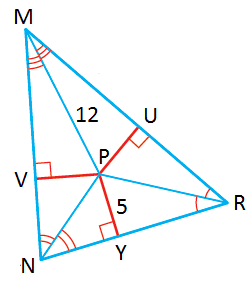

الحل:

نظريةُ فيثاغورس	${\left(MP\right)}^2 = {\left(MV\right)}^2 + {\left(VP\right)}^2$
بتعويضِ $MP = 12 , VP = 5$	${\left(12\right)}^2 = {\left(MV\right)}^2 + {\left(5\right)}^2$
بإيجادِ القوى	$144 = {\left(MV\right)}^2 + 25$$$
بطرحِ 25 منْ طرفيِ المعادلةِ	${\left(MV\right)}^2 = 119$
بأخذِ الجذرِ التربيعيِّ لطرفيِ المعادلةِ	$MV = \pm \sqrt{119}$

بما أنَّ الطول لا يُمكِنُ أنْ يكون سالبًا ، فإنَّ $MV = \sqrt{119}$